Презентація на тему «Задачі Наполеона»

Задачі Наполеона

Коротко про Наполеона

Наполеон I Бонапарт (італ. Napoleone Buonaparte, фр. Napoléon Bonaparte, 15 серпня 1769, Аяччо, Корсика - 5 травня 1821, Лонгвуд, о. Святої Єлени) - імператор Французів в 1804-1815 рр.., Французький полководець і державний діяч, який заклав основи сучасного французького держави.

Французький імператор Наполеон Бонапарт був любителем математики. Він знаходив час займатися нею для власного задоволення, відчував у ній красу і об'єкт, гідний додатка дотепності та винахідливості. Одне зі свідчень тому-кілька, складених їм геометричних задач.

Перша задача
На сторонах довільного трикутника АВС зовнішнім чином побудовані як на підставах рівносторонні трикутники. Довести, що центри цих трикутників також є вершинами рівностороннього трикутника.
Рішення
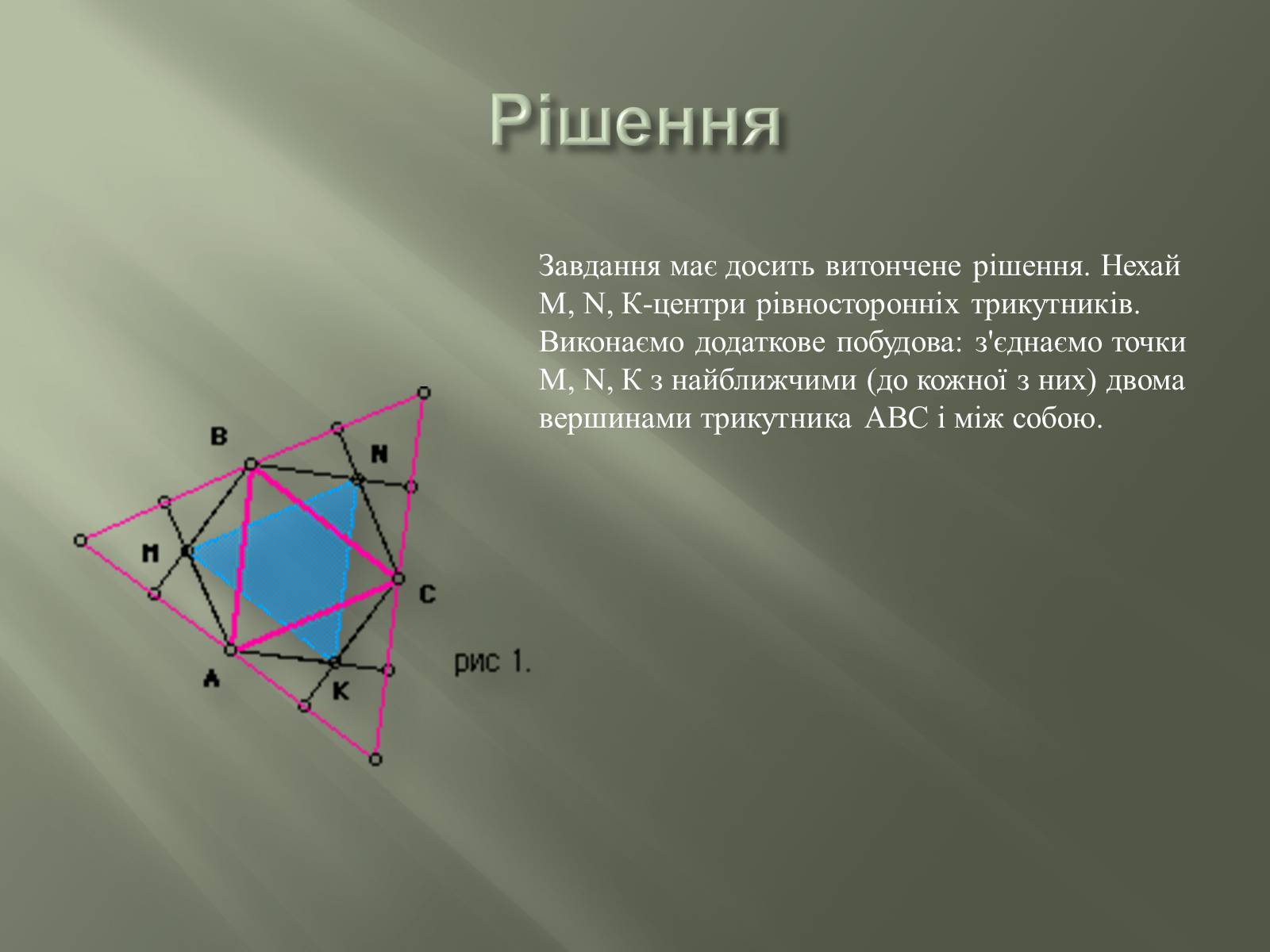
Завдання має досить витончене рішення. Нехай М, N, К-центри рівносторонніх трикутників. Виконаємо додаткове побудова: з'єднаємо точки М, N, К з найближчими (до кожної з них) двома вершинами трикутника АВС і між собою.
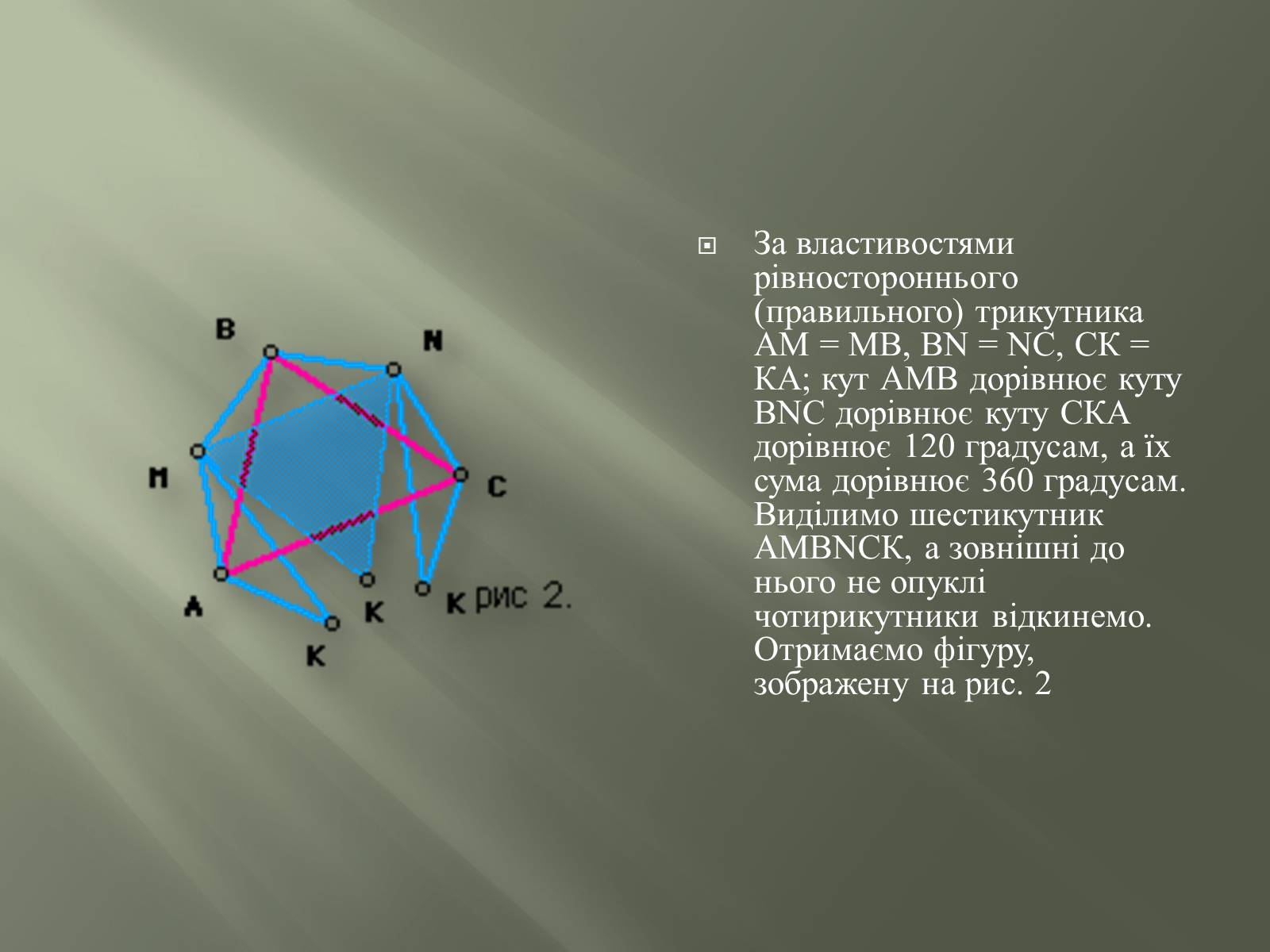
За властивостями рівностороннього (правильного) трикутника АМ = МВ, ВN = NC, СК = КА; кут АМВ дорівнює куту ВNС дорівнює куту СКА дорівнює 120 градусам, а їх сума дорівнює 360 градусам. Виділимо шестикутник АМВNСК, а зовнішні до нього не опуклі чотирикутники відкинемо. Отримаємо фігуру, зображену на рис. 2
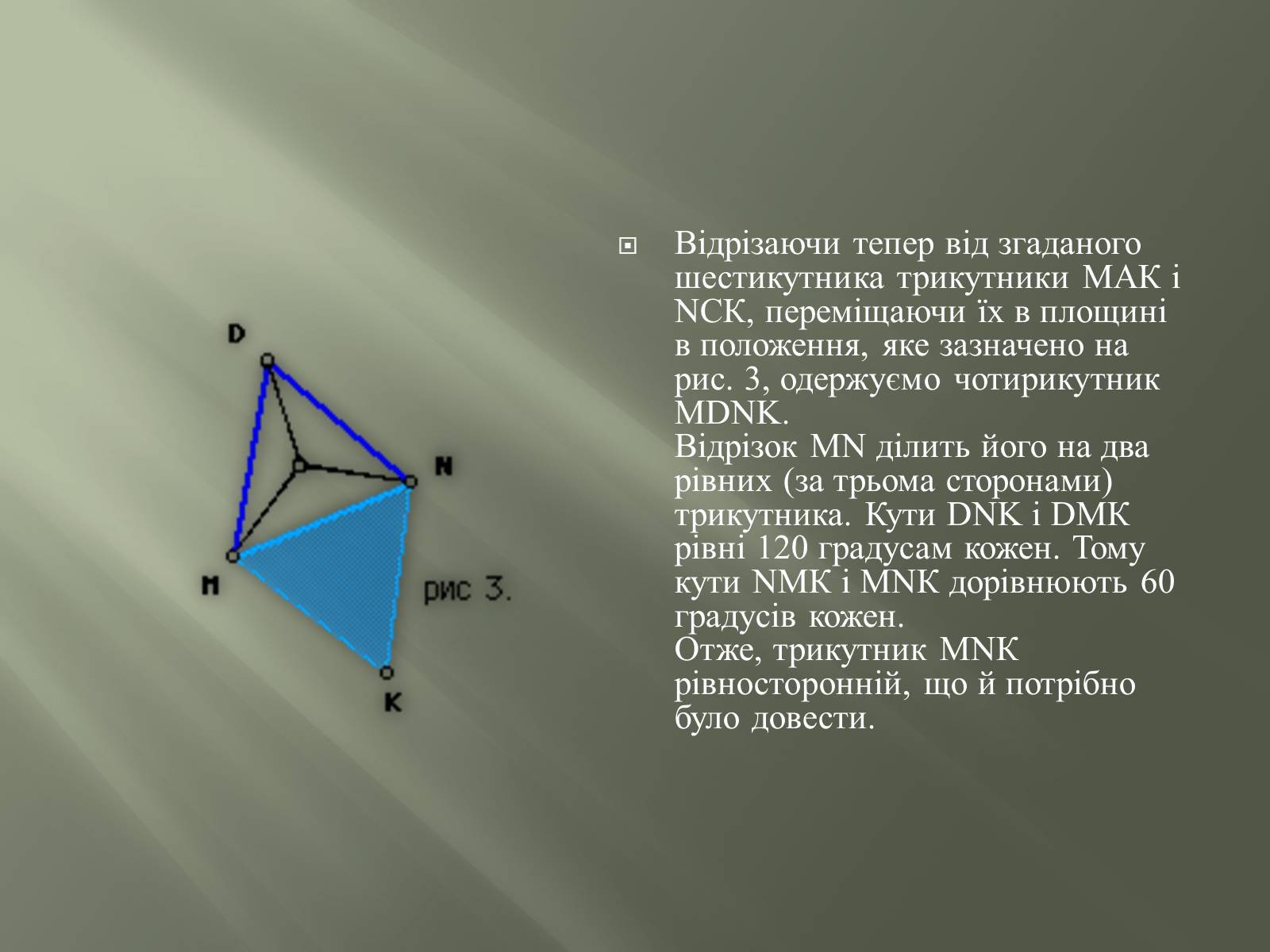
Відрізаючи тепер від згаданого шестикутника трикутники МАК і NСК, переміщаючи їх в площині в положення, яке зазначено на рис. 3, одержуємо чотирикутник МDNK.Відрізок МN ділить його на два рівних (за трьома сторонами) трикутника. Кути DNK і DМК рівні 120 градусам кожен. Тому кути NМК і МNК дорівнюють 60 градусів кожен.Отже, трикутник МNК рівносторонній, що й потрібно було довести.

Друга задача
У трикутнику ABC знайти точку P, таку що сума відстаней від P до вершин A, B і C мінімальна.

Рішення
Найбільш просте рішення Наполеон Бонапарт знайшов у бутність свою кадетом артилерійського училища. Цей спосіб накладає єдине обмеження: найбільший кут трикутника повинен бути менше 120 град.Нехай F - довільна точка всередині трикутника. Повернемо трикутник ABF навколо вершини B назовні на 60 `.У цьому випадку AF = A'F 'і BF = B'F' з побудови, BF = F'F, тому що трикутник BFF 'рівносторонній, значить сума відстаней від F до A, B, C дорівнює довжині ламаної A'F' FC.

Ця сума стане мінімальною, якщо прийме таке положення,що ламана стане прямою.Для цього потрібно, щоб ділянкаAF'F стала прямою, тобто щоб A'F'B і,отже, AFB дорівнював120.Ще потрібно, щоб ділянка F'Fcстала прямою, тобто щоб BFC дорівнював120. Третій кут при точці F автоматично стане рівним 120. Отже, доведено, що всі три кути при шуканої точці F рівні.

Наполеон був видатним полководцем і державним діячем, але у нього завжди був час на математику. Своїми знаннями в галузі математики він вражав таких відомих французьких математиків того часу як Лагранж і Лаплас.

Дякую за увагу!