Презентація на тему «Види правильних многогранників» (варіант 1)

Види правильнихмногогранників
Підготувала Драганчук Ольга

Правильним многогранником є многогранник, грані якого є правильними многокутниками з рівною кількістю сторін, а в кожній вершині многогранника сходиться однакова кількість ребер.

Існує п'ять типів
правильних
опуклих многогранників:
Тетраедр
Куб
Октаедр
Додекаедр
Ікосаедр.

У правильного многогранника:- усі ребра рівні;- усі двогранні кути, що містять дві грані зі спільним ребром, також рівні.

У правильного тетраедра всі чотири грані – рівносторонні трикутники. Кожна з його вершин є вершиною трьох трикутників. Сума плоских кутів при кожній із вершин дорівнює 180 градусам. Правильний тетраедр не має центра симетрії.
Тетраедр

У правильного октаедра всі вісім граней – рівносторонні трикутники. Кожна вершина октаедра є вершиною чотирьох трикутників. Сума кутів плоских кутів при кожній вершині дорівнює двомстам сорока градусам. Правильний октаедр має центр симетрії.
Октаедр
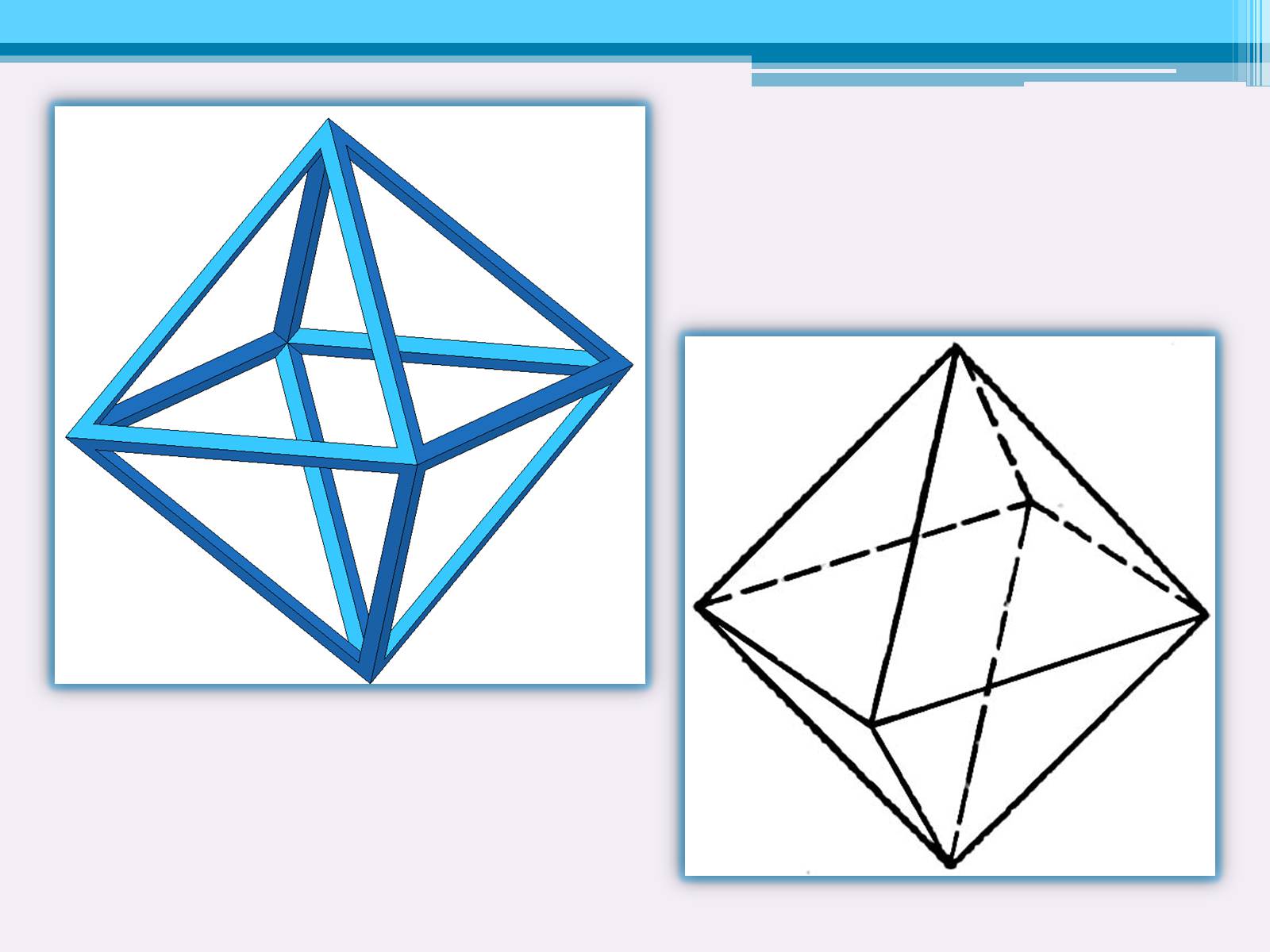
У правильного октаедра всі вісім граней – рівносторонні трикутники. Кожна вершина октаедра є вершиною чотирьох трикутників. Сума кутів плоских кутів при кожній вершині дорівнює двомстам сорока градусам. Правильний октаедр має центр симетрії.
Октаедр

У правильного ікосаедра всі двадцять граней – рівносторонні трикутники. Кожна з вершин ікосаедра є вершиною п'яти трикутників. Сума плоских кутів при кожній з вершин ікосаедра дорівнює трьомстам градусам. Правильний ікосаедр має центр симетрії.
Ікосаедр
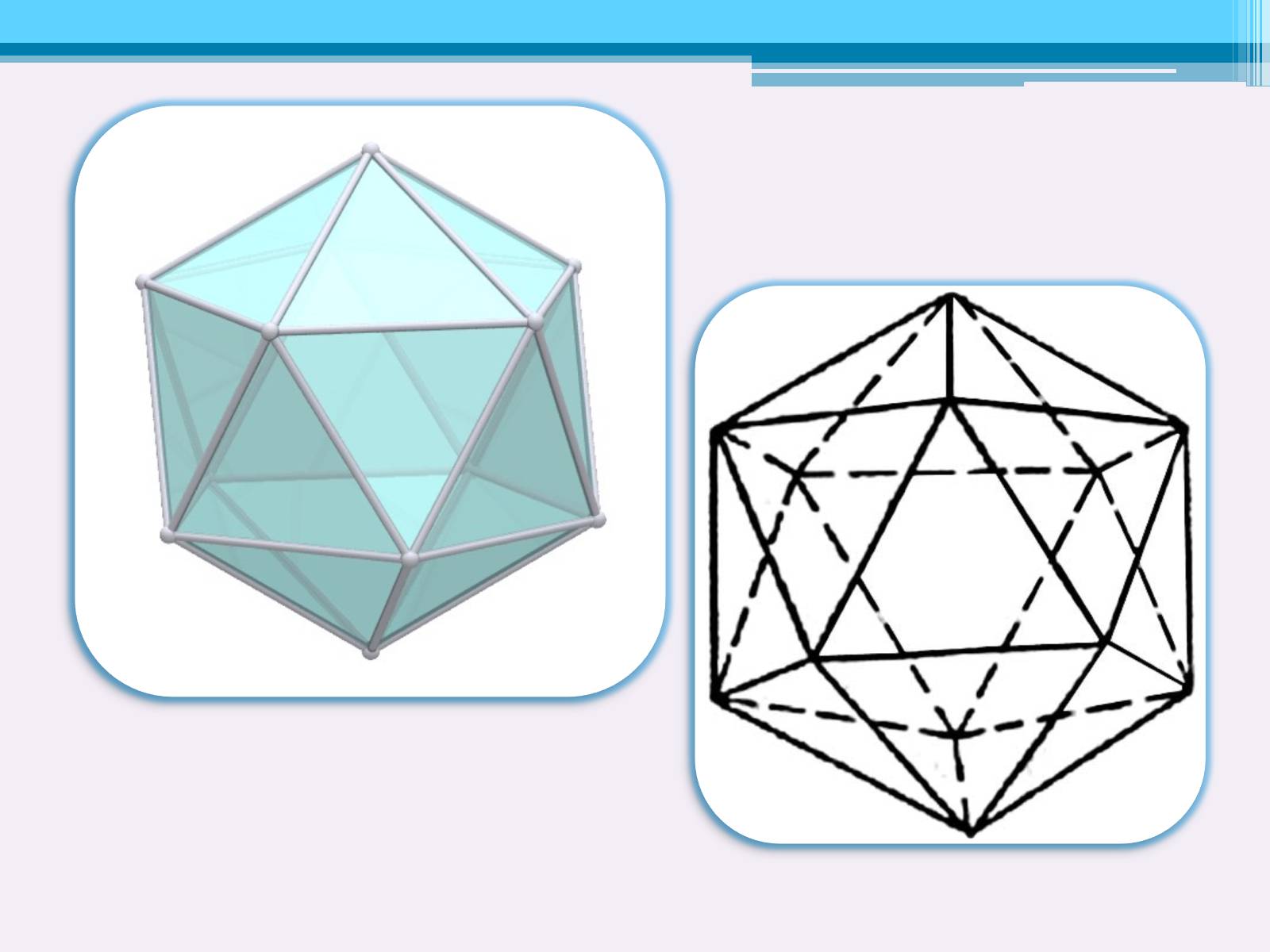
У правильного ікосаедра всі двадцять граней – рівносторонні трикутники. Кожна з вершин ікосаедра є вершиною п'яти трикутників. Сума плоских кутів при кожній з вершин ікосаедра дорівнює трьомстам градусам. Правильний ікосаедр має центр симетрії.
Ікосаедр

У куба всі шість граней – квадрати. Кожна з вершин куба є вершиною трьох квадратів. Сума плоских кутів при кожній з вершин куба дорівнює двомстам сімдесяти градусам. Куб має один центр симетрії.
Куб
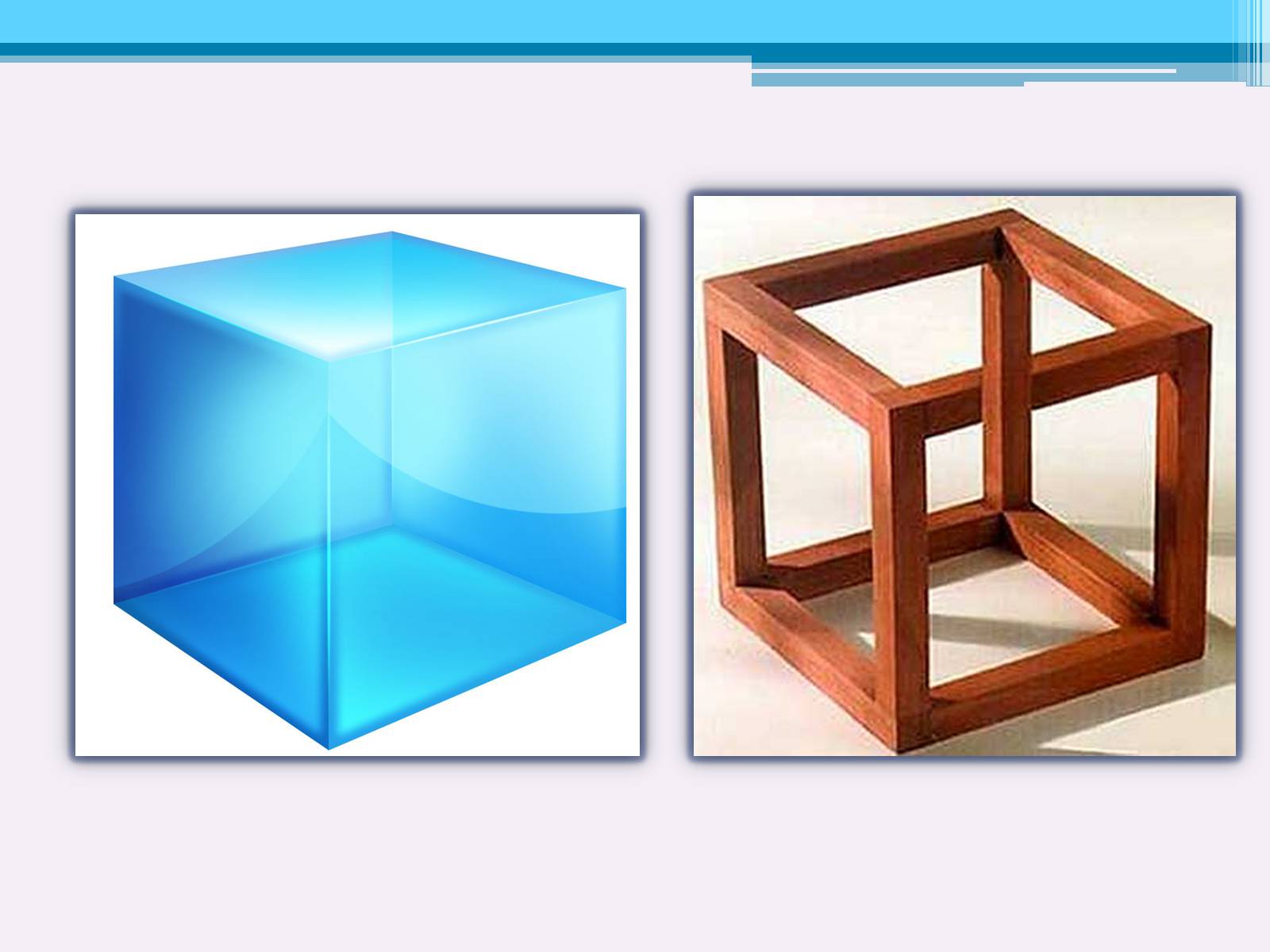
У куба всі шість граней – квадрати. Кожна з вершин куба є вершиною трьох квадратів. Сума плоских кутів при кожній з вершин куба дорівнює двомстам сімдесяти градусам. Куб має один центр симетрії.
Куб

У правильного додекаедра всі дванадцять граней – правильні п'ятикутники. Кожна з вершин додекаедра є вершиною трьох правильних п'ятикутників. Сума плоских кутів при кожній з вершин дорівнює трьомстам двадцяти чотирьом градусам. Правильний додекаедр має центр симетрії.
Додекаедр
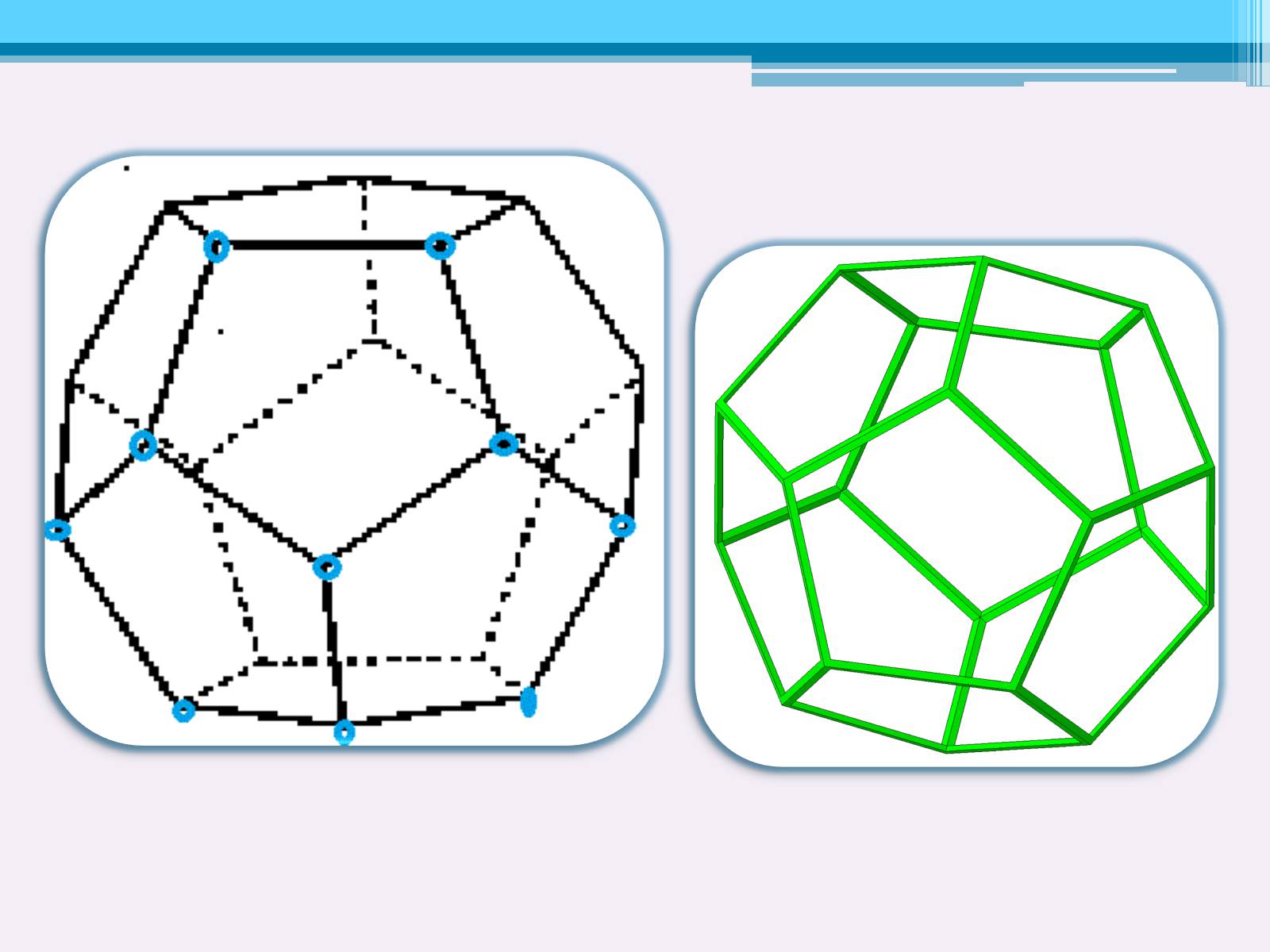
У правильного додекаедра всі дванадцять граней – правильні п'ятикутники. Кожна з вершин додекаедра є вершиною трьох правильних п'ятикутників. Сума плоских кутів при кожній з вершин дорівнює трьомстам двадцяти чотирьом градусам. Правильний додекаедр має центр симетрії.
Додекаедр

Інших видів правильних многогранників НЕ існує. Не існує правильного многогранника, гранями якого є правильні шестикутники, семикутники і взагалі n-кутники з кількістю сторін, більшою за п'ять.