Презентація на тему «Трикутник»

Трикутник та його елементиРівность трикутників

Мета :
1. Домогтися засвоєння учнями змісту понять “трикутник”; ”сторони, кути , вершини”, “кут, протилежний стороні”, “кут, прилеглий до сторони”, “рівні трикутники” та ознак рівності трикутників.
2. Формувати уміння учнів розпізнавати та називати елементи трикутників, зображених на рисунку .
3. Розвивати логічне мислення, уяву, математичну мову учнів.
4. Розв'язувати задачі на обчислення сторін трикутника за відомим периметром і навпаки, та задачі на доведення, використовуючи ознаки рівності трикутників.

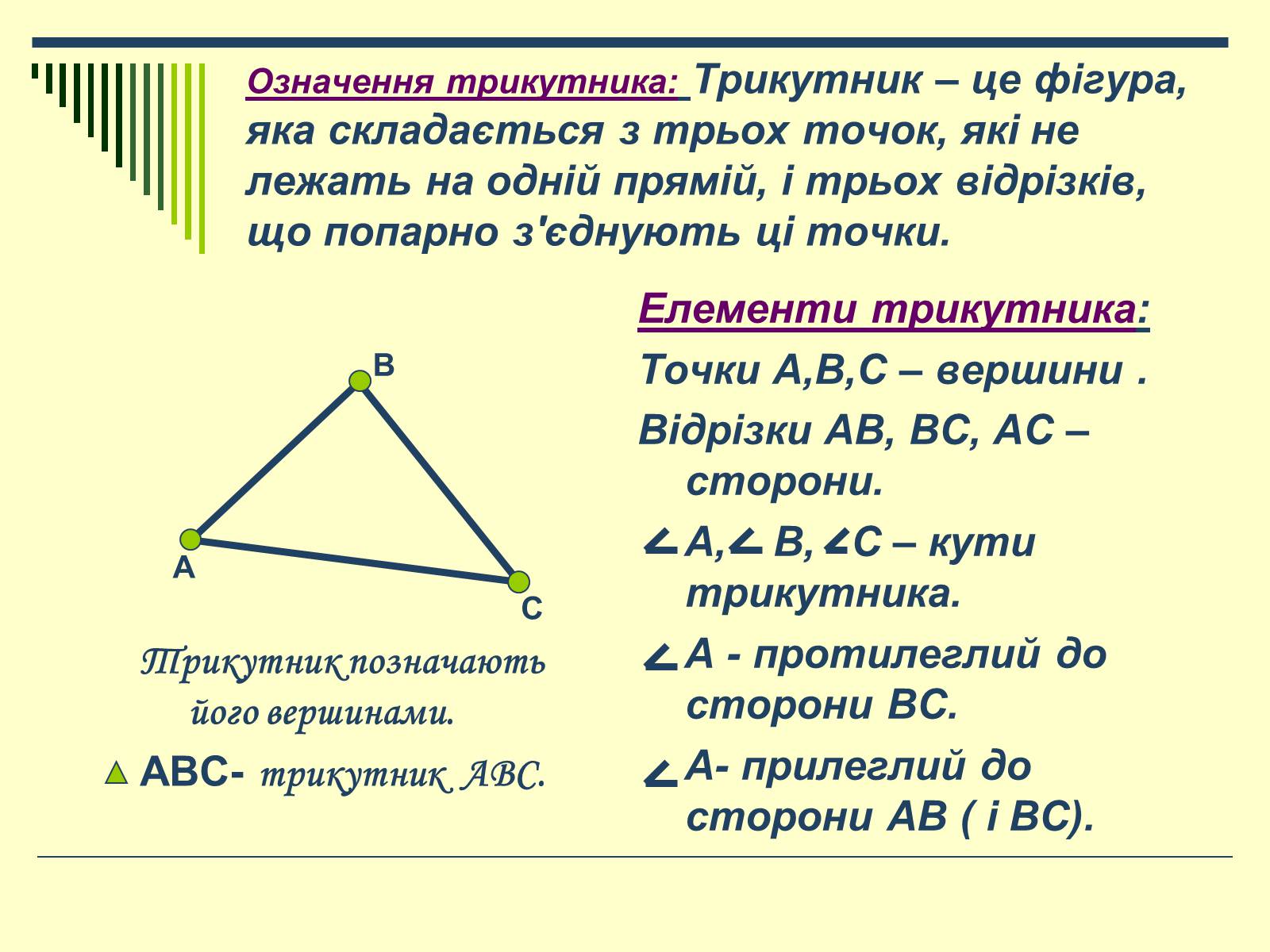
Означення трикутника: Трикутник – це фігура, яка складається з трьох точок, які не лежать на одній прямій, і трьох відрізків, що попарно з'єднують ці точки.
Трикутник позначають його вершинами.
АВС- трикутник АВС.
Елементи трикутника:
Точки А,В,С – вершини .
Відрізки АВ, ВС, АС – сторони.
А, В, С – кути трикутника.
А - протилеглий до сторони ВС.
А- прилеглий до сторони АВ ( і ВС).
В
С
А

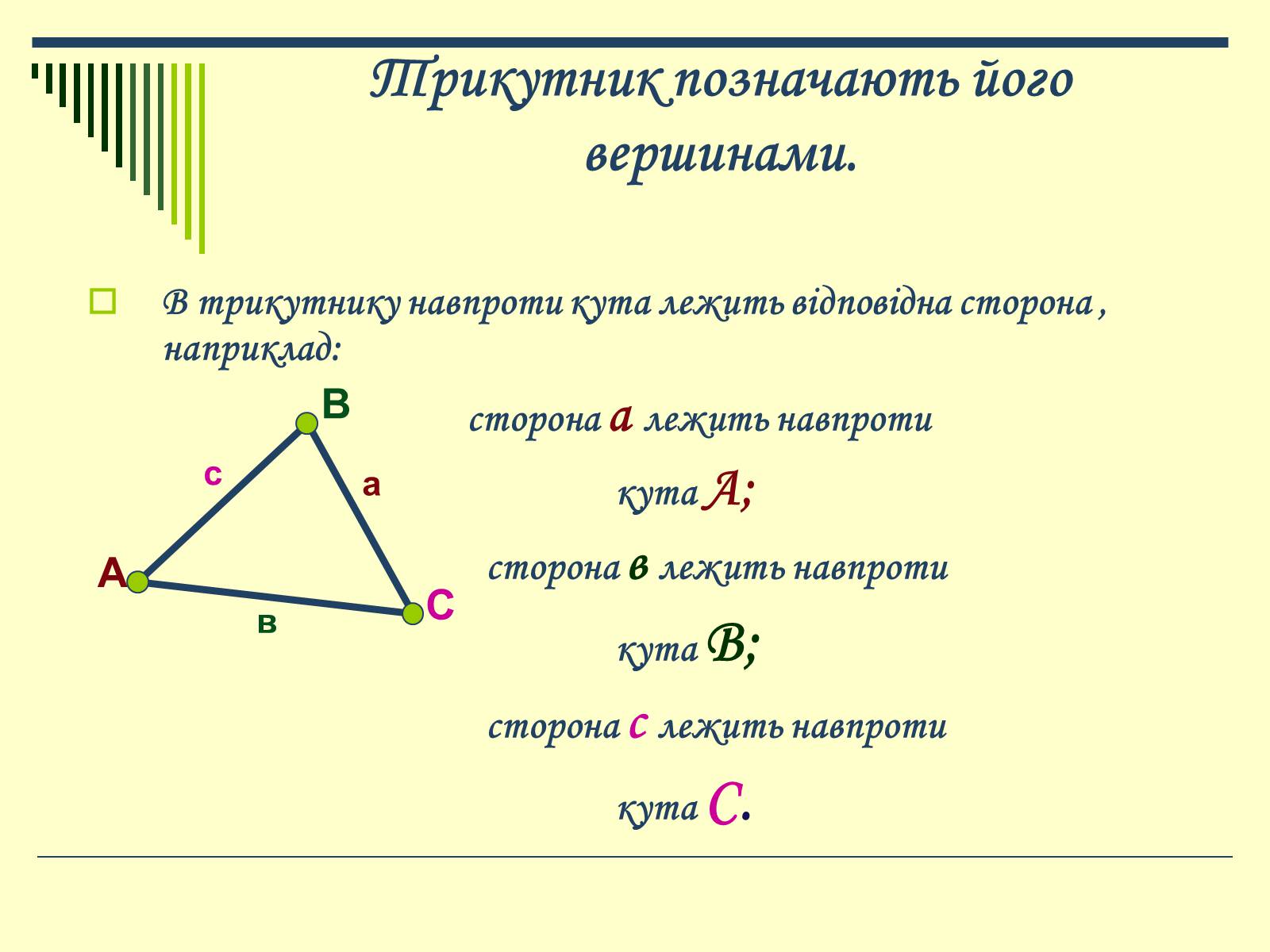
Трикутник позначають його вершинами.
В трикутнику навпроти кута лежить відповідна сторона , наприклад:
сторона а лежить навпроти
кута А;
сторона в лежить навпроти
кута В;
сторона с лежить навпроти
кута С.
А
В
С
а
в
с

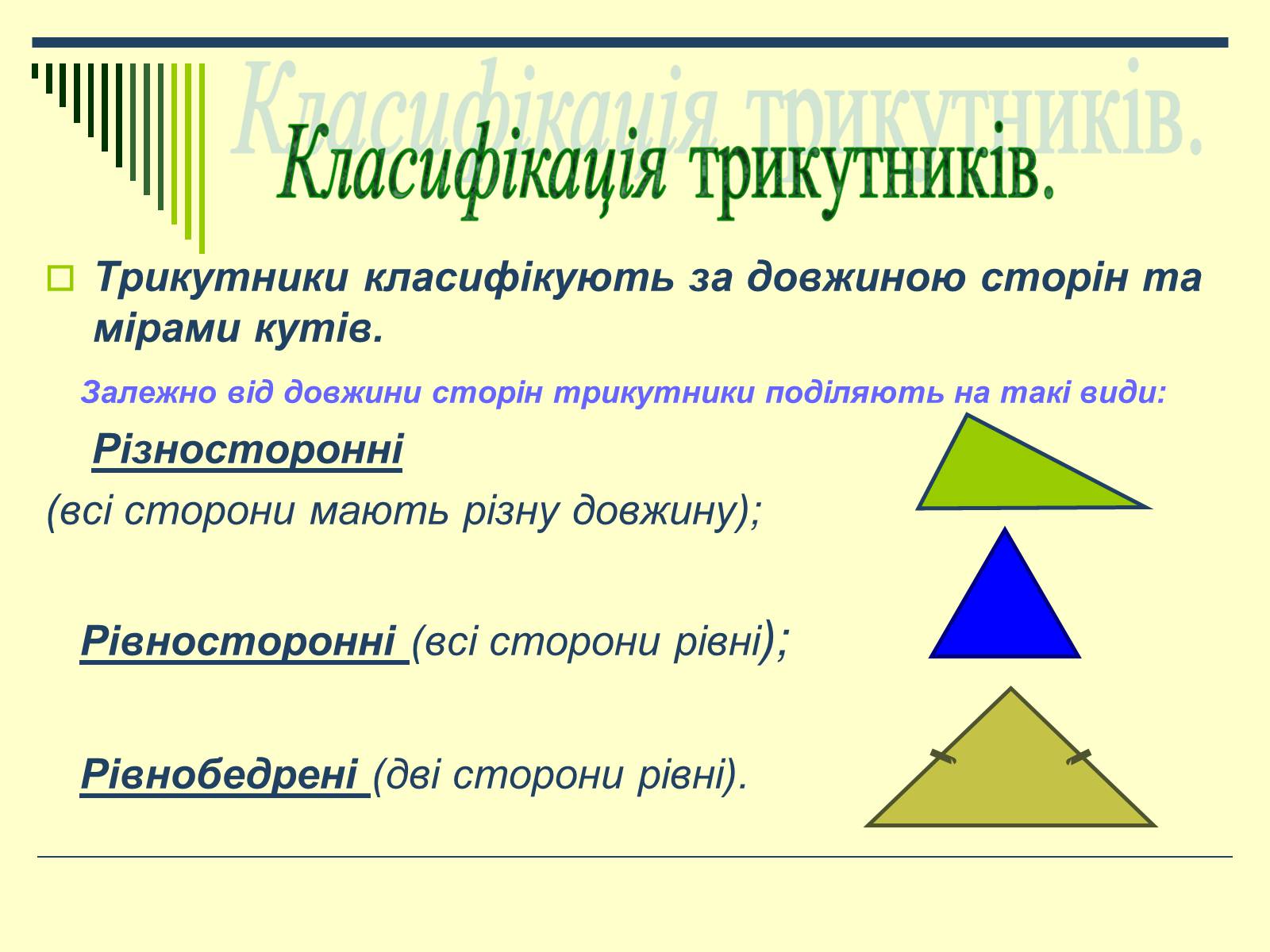
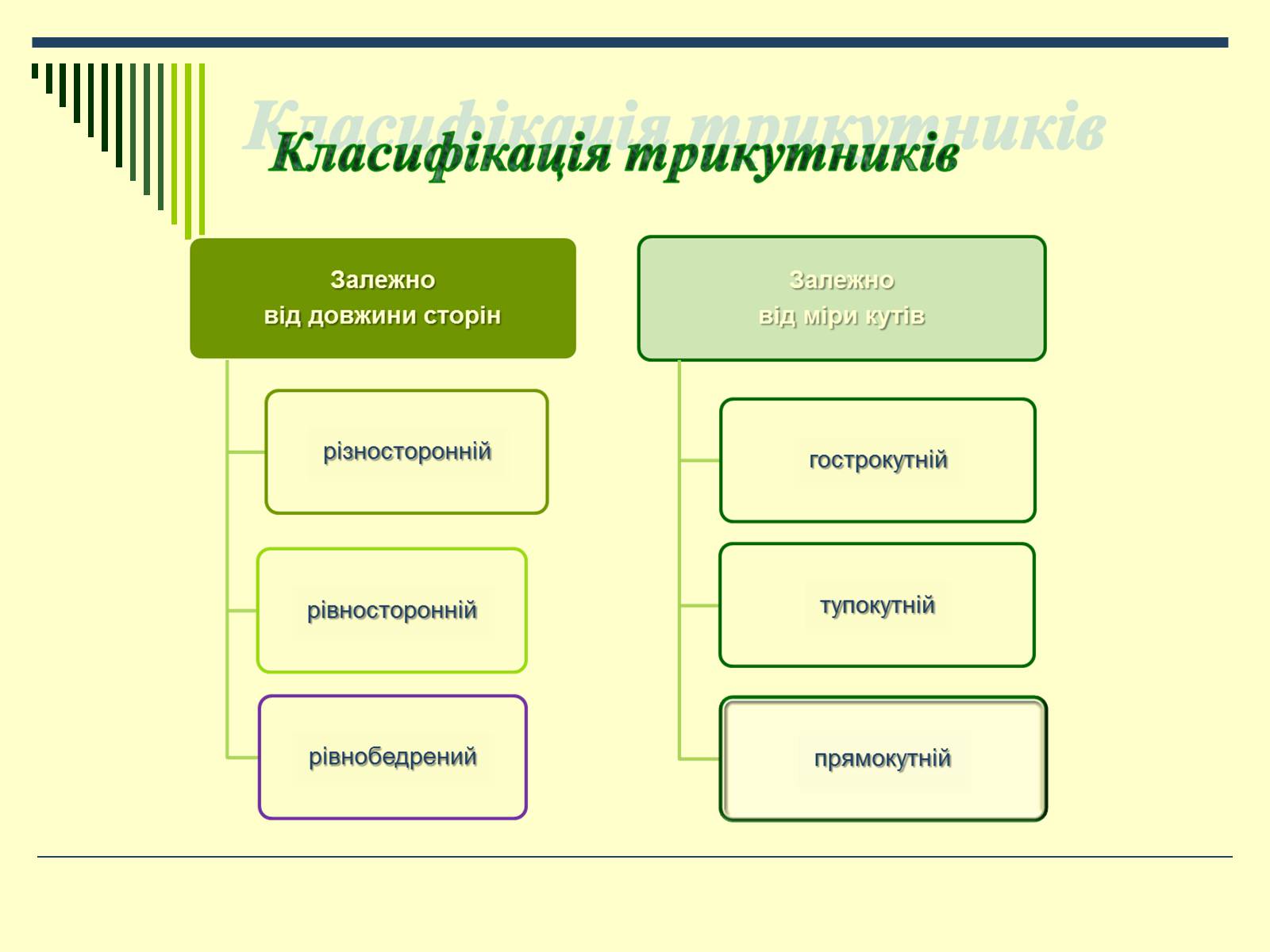
Трикутники класифікують за довжиною сторін та мірами кутів.
Залежно від довжини сторін трикутники поділяють на такі види:
Різносторонні
(всі сторони мають різну довжину);
Рівносторонні (всі сторони рівні);
Рівнобедрені (дві сторони рівні).

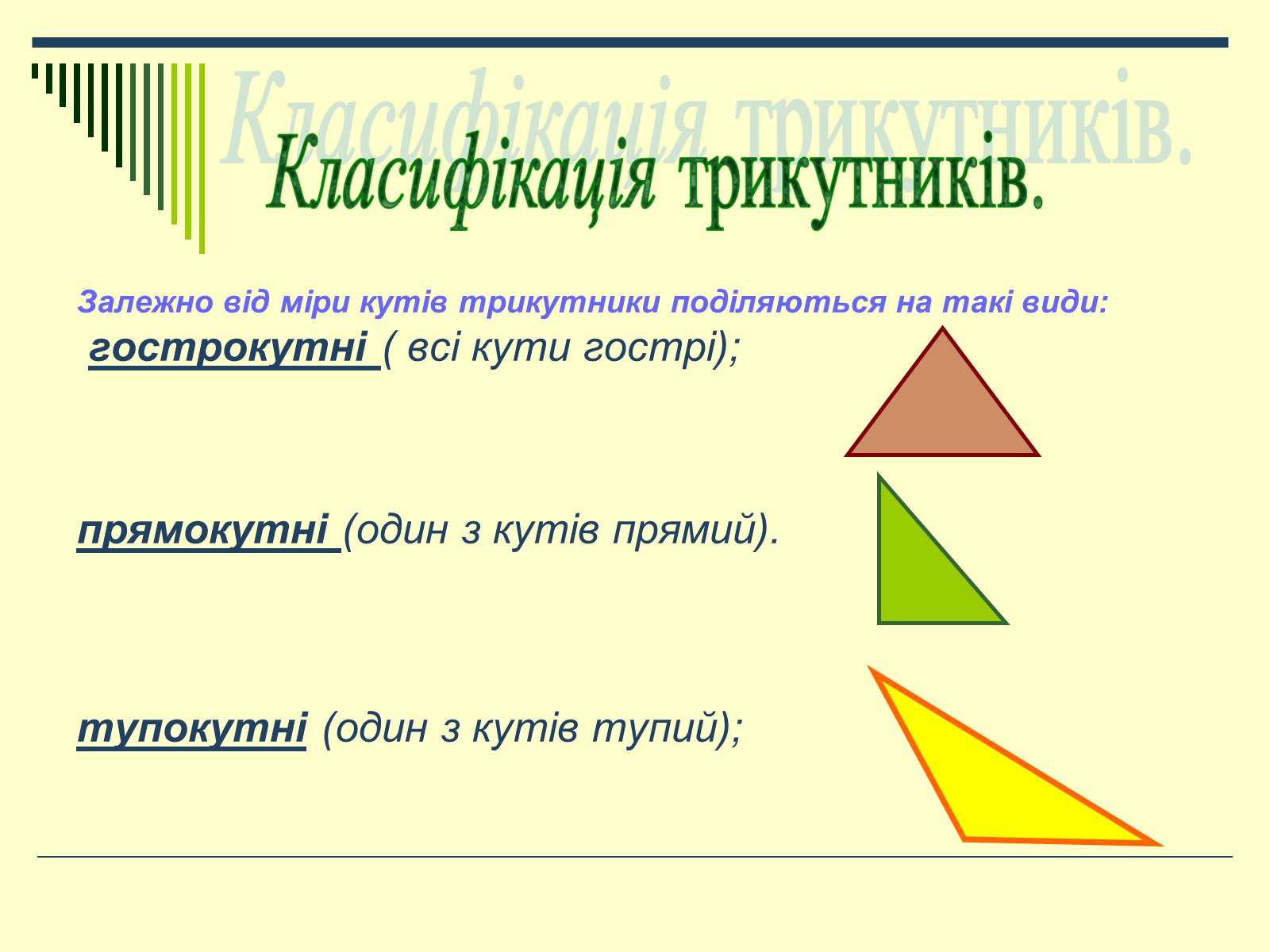
Залежно від міри кутів трикутники поділяються на такі види:
гострокутні ( всі кути гострі);
прямокутні (один з кутів прямий).
тупокутні (один з кутів тупий);

Залежно від міри кутів трикутники поділяються на такі види:
гострокутні ( всі кути гострі);
прямокутні (один з кутів прямий).
тупокутні (один з кутів тупий);

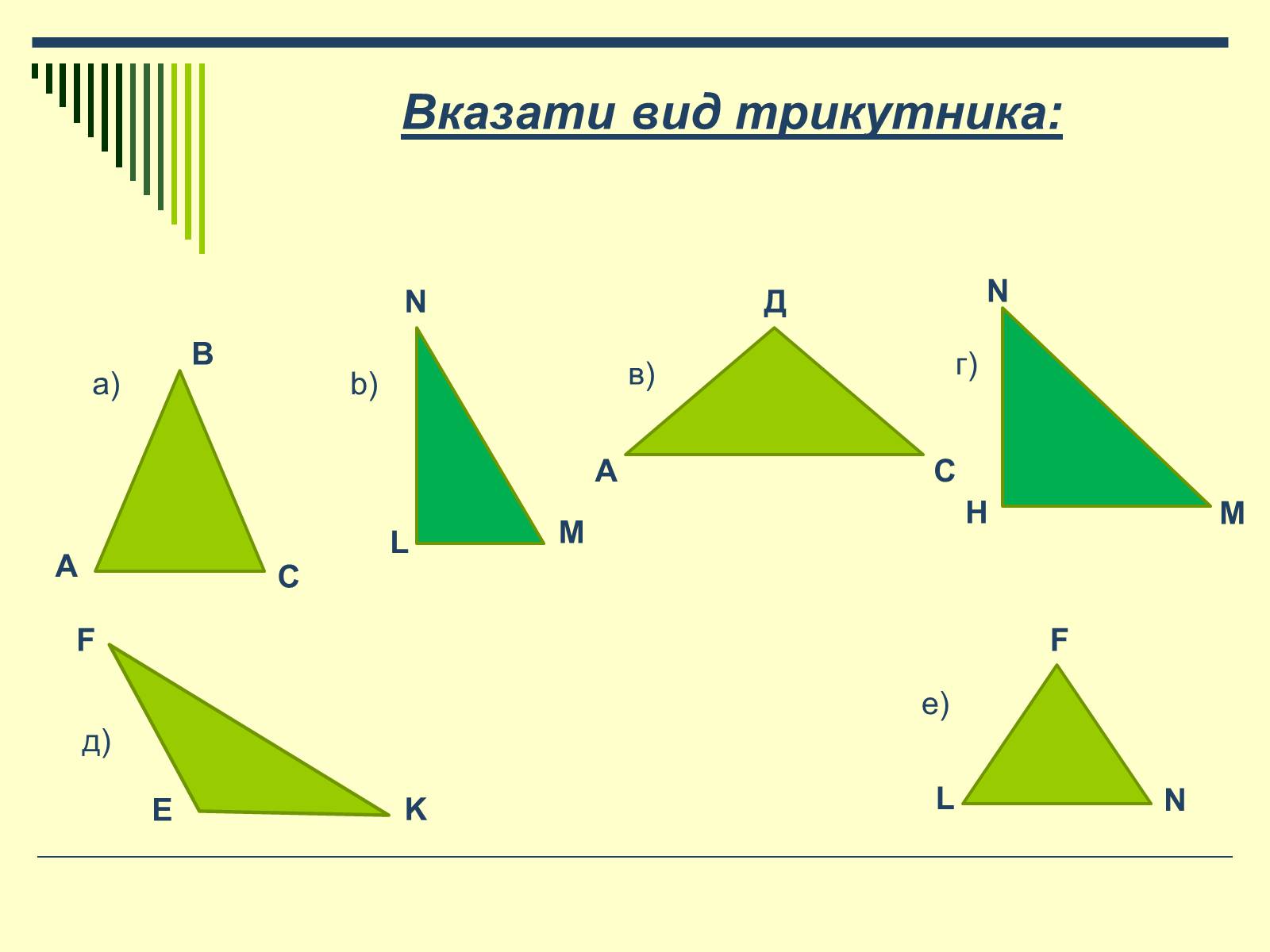
Вказати вид трикутника:
А
В
С
а)
N
L
M
b)
А
Д
С
в)
г)
H
N
M
F
E
K
L
F
N
д)
е)

Що знали про
трикутники в далеку давнину?
Уже кілька тисяч років тому єгиптяни знали, що коли сторони трикутника дорівнюють 3, 4 і 5 одиничним відрізкам, то такий трикутник прямокутний.
Землеміри Стародавнього Єгипту для побудови прямого кута ділили мотузку вузликами на 12 рівних частин і кінці зав'язували. Потім мотузку розтягували на землі так, щоб утворився трикутник зі сторонами по 3, 4 і 5 поділок. Більший з кутів утвореного трикутника – прямий.
Ребра бічних граней єгипетських пірамід утворюють майже рівносторонні
трикутники.

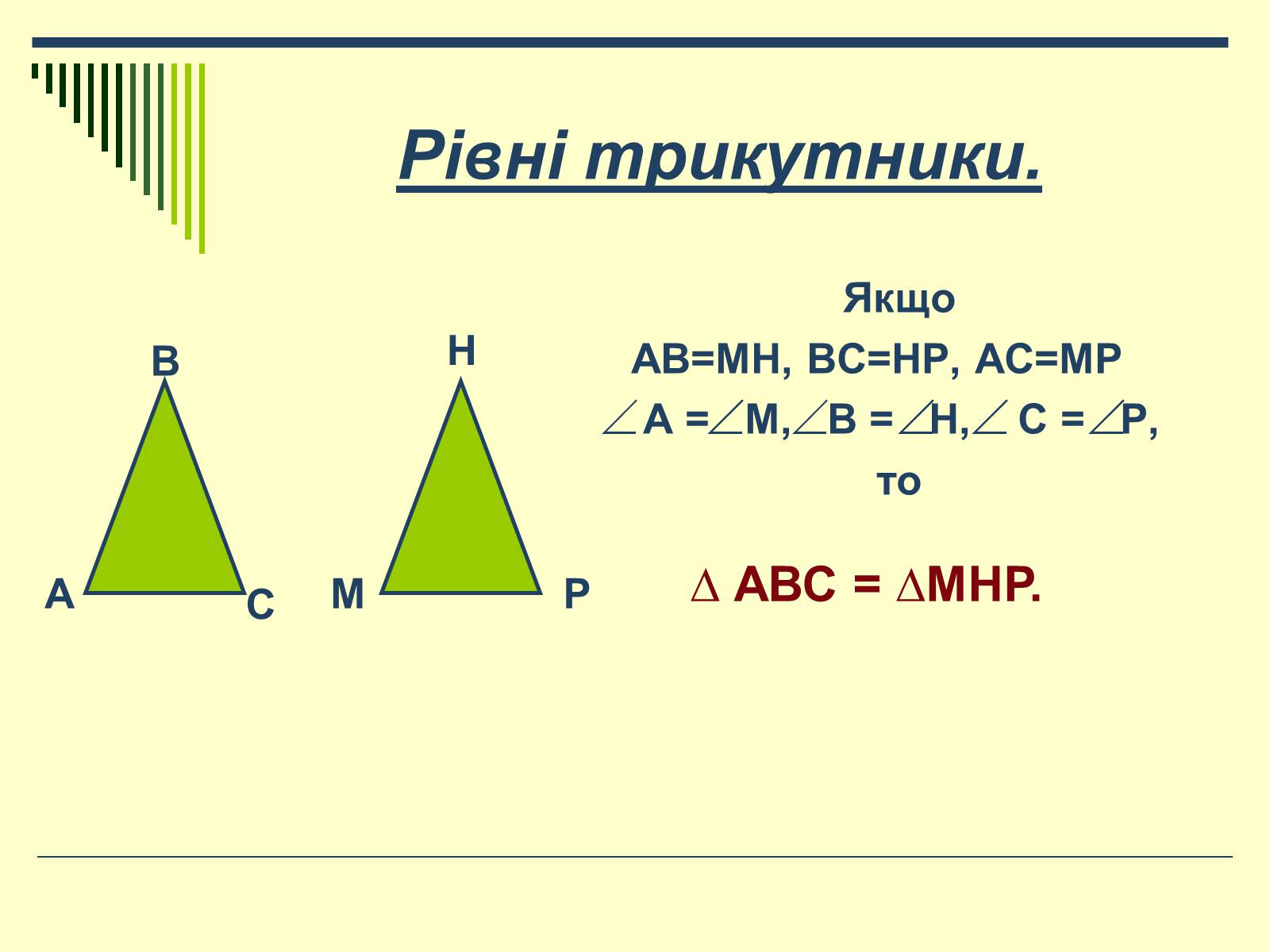
Рівні трикутники.
Якщо
АВ=МН, ВС=НР, АС=МР
А = М, В = Н, С = Р,
то
А
В
С
М
Н
Р
∆ АВС = ∆МНР.

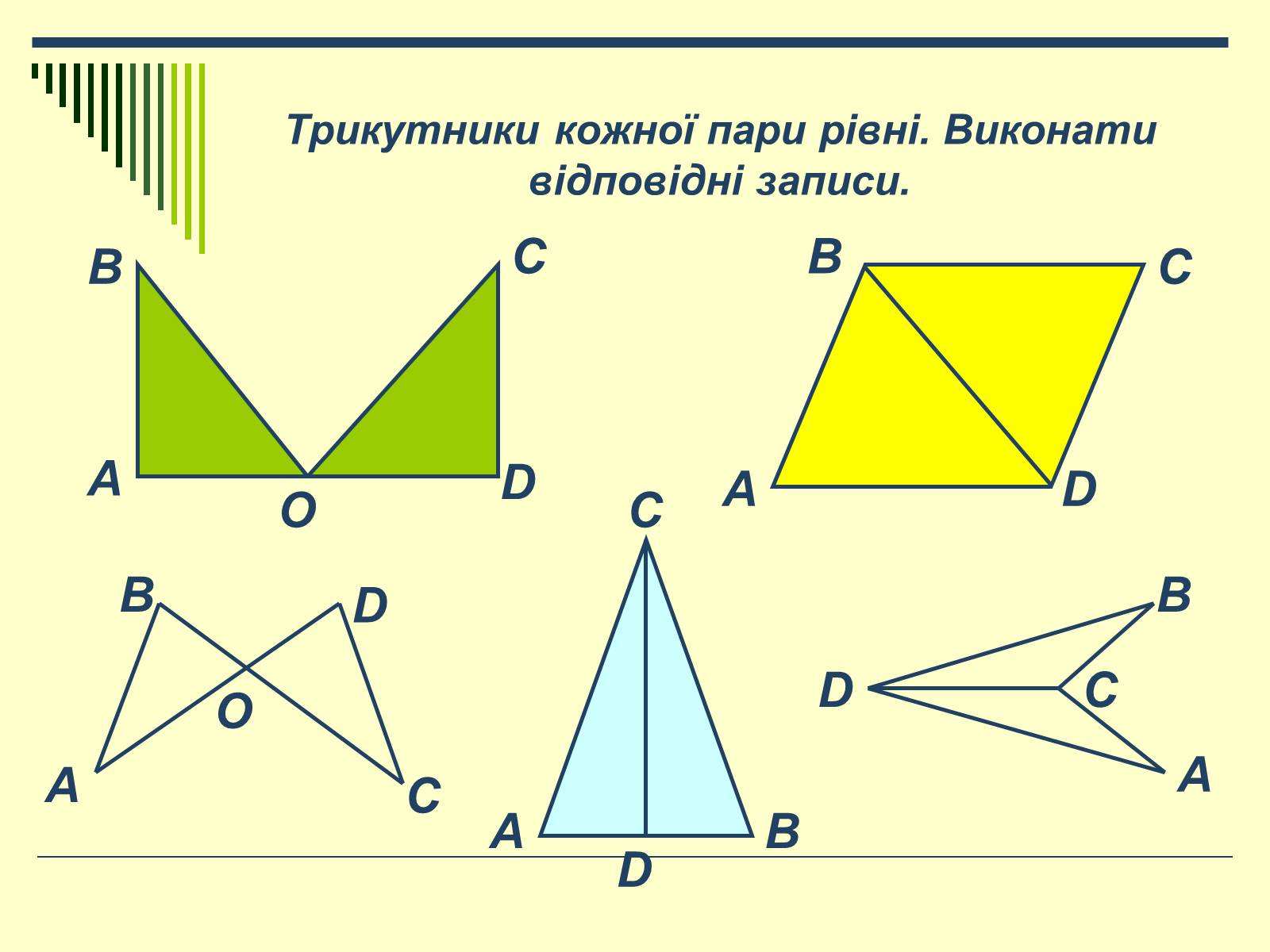
Трикутники кожної пари рівні. Виконати відповідні записи.
А
А
А
А
А
В
В
В
В
В
С
С
С
С
С
D
D
D
D
D
O
O

Задача:
Відомо, що ∆ ABC= ∆ MKN. Знайти :
а) кут К, якщо В=125 ;
б) Сторону АВ, якщо КМ=11 см;
в) Периметр ∆ MKN, якщо АВ=11 см, MN=8см, KN=7см.

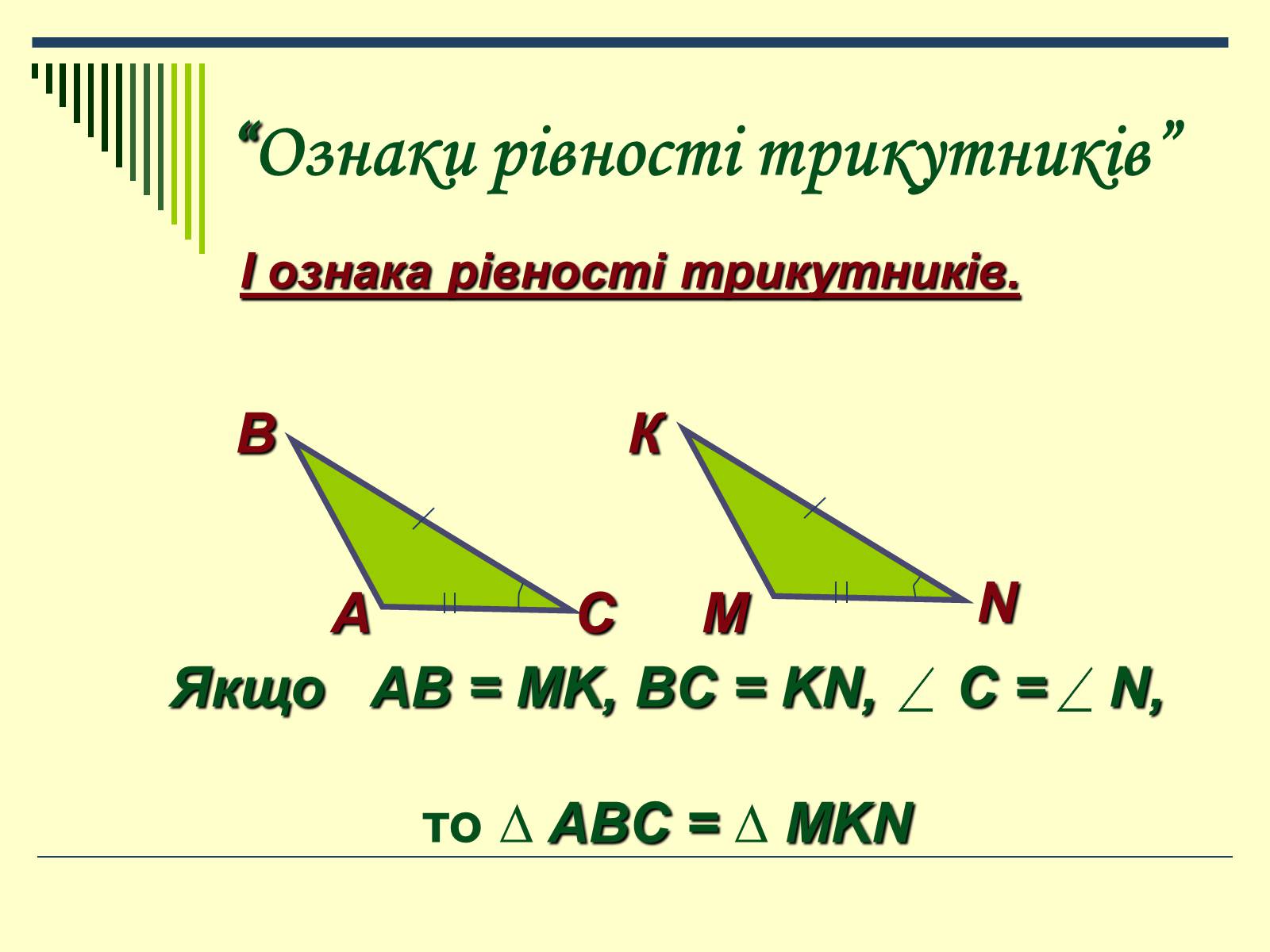
“Ознаки рівності трикутників”
І ознака рівності трикутників.
А
В
С
К
М
N
Якщо AB = MK, BC = KN, C = N,
то ∆ ABC = ∆ MKN

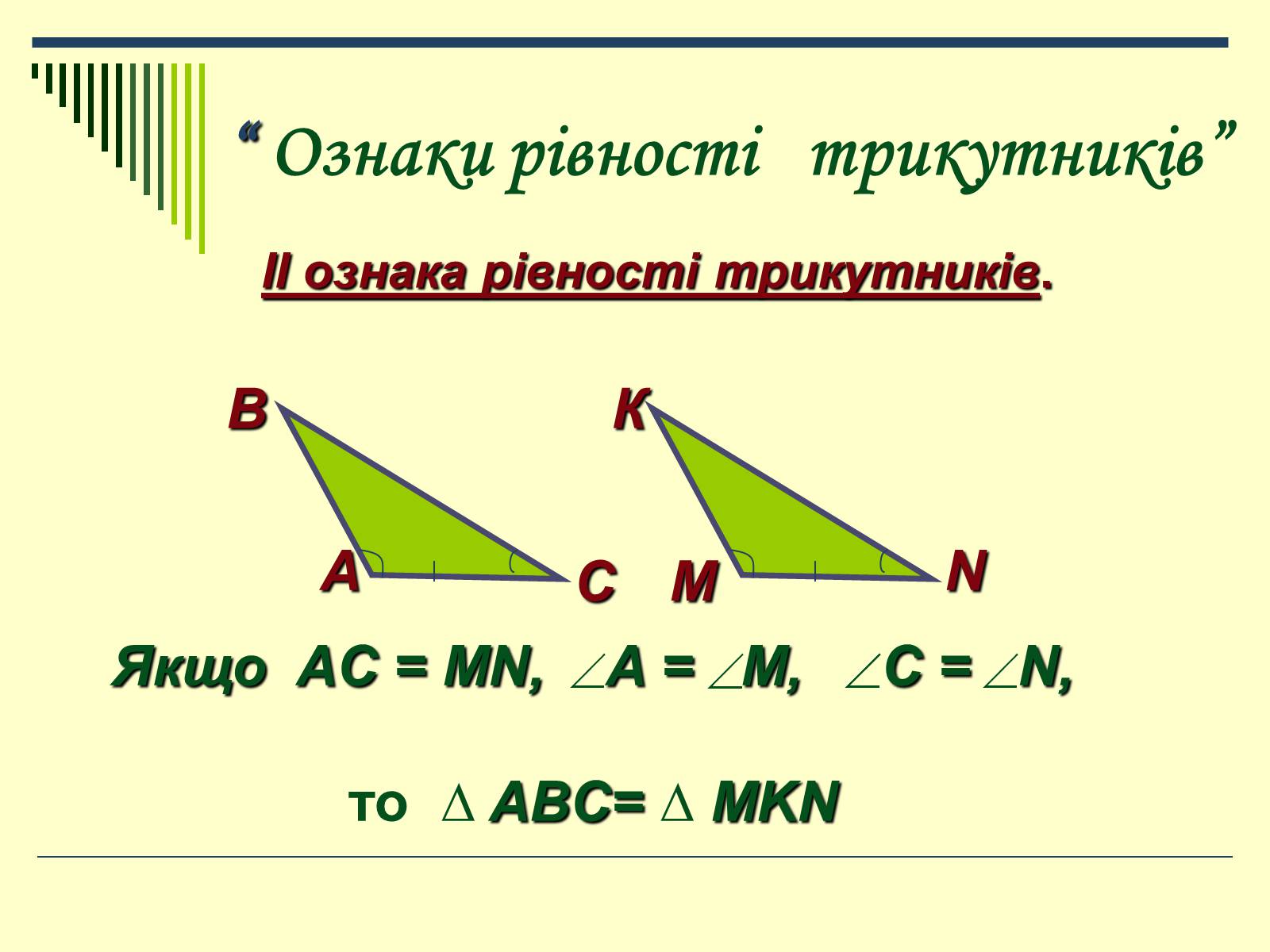
“ Ознаки рівності трикутників”
ІІ ознака рівності трикутників.
В К
С
М
N
А
Якщо AC = MN, A = M, C = N,
то ∆ ABC= ∆ MKN

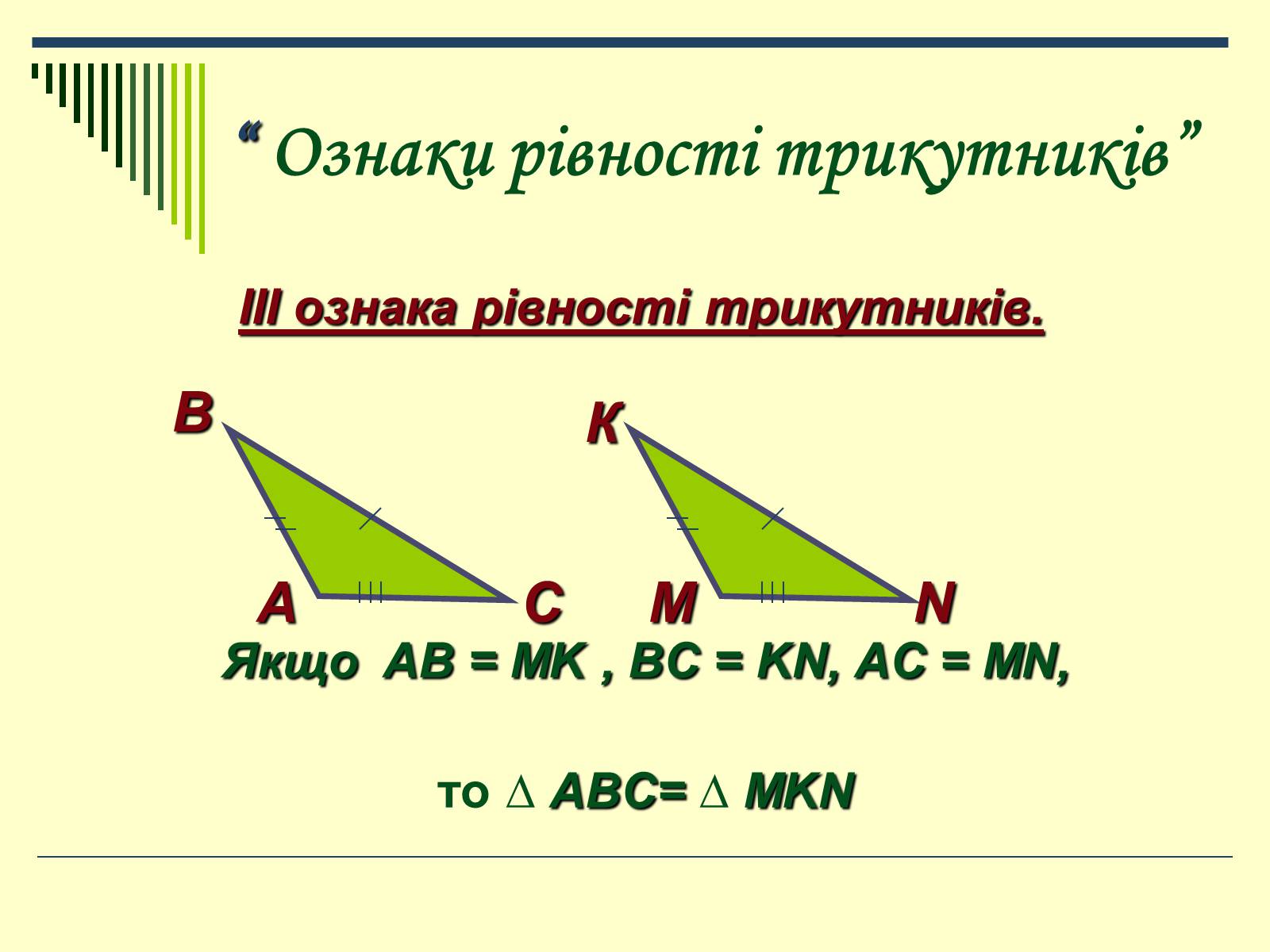
“ Ознаки рівності трикутників”
ІІІ ознака рівності трикутників.
Якщо AB = MK , BC = KN, AC = MN,
то ∆ ABC= ∆ MKN
К
М
N
А
В
С

В
А
С
а) Дано: ∆АВС. АВ = ВС, АВ = 4 см,
АС на 3 см більша за АВ.
Знайти : Р.
б) Дано: ∆АВС. АВ = ВС, АВ = 8 см,
АС в два рази менша за АВ.
Знайти : Р.
в) Знайти сторони ∆АВС, якщо
АВ : ВС : АС = 2 : 2 : 4, а периметр
дорівнює 56 см.
Розв'язування вправ на знаходження невідомих елементів трикутника.

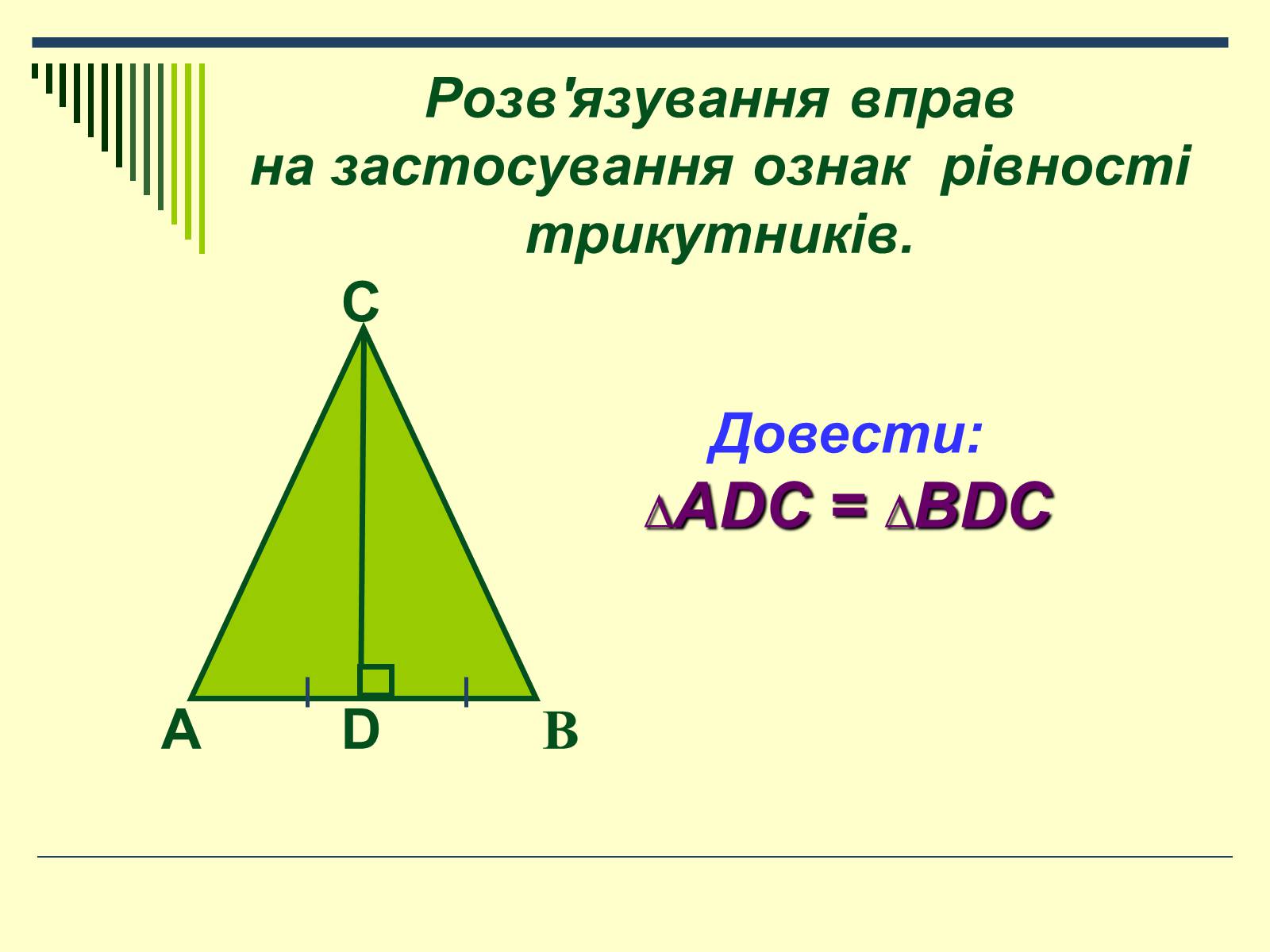
Розв'язування вправ на застосування ознак рівності трикутників.
B
A
D
C
Довести:
∆ADC = ∆BDC

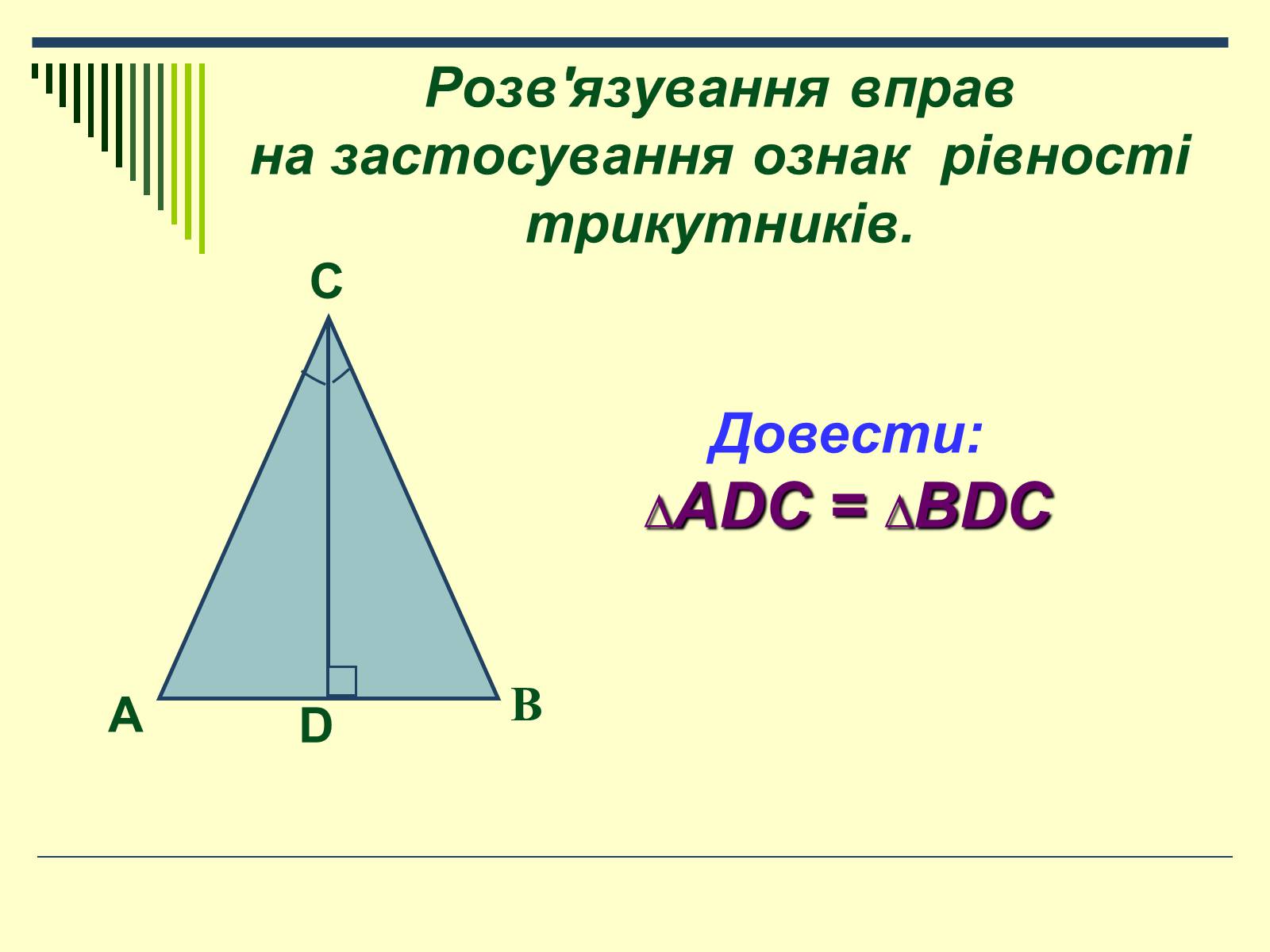
Розв'язування вправ на застосування ознак рівності трикутників.
Довести:
∆ADC = ∆BDC
A
D
B
C

Розв'язування вправ на застосування ознак рівності трикутників.
O
D
B
A
C
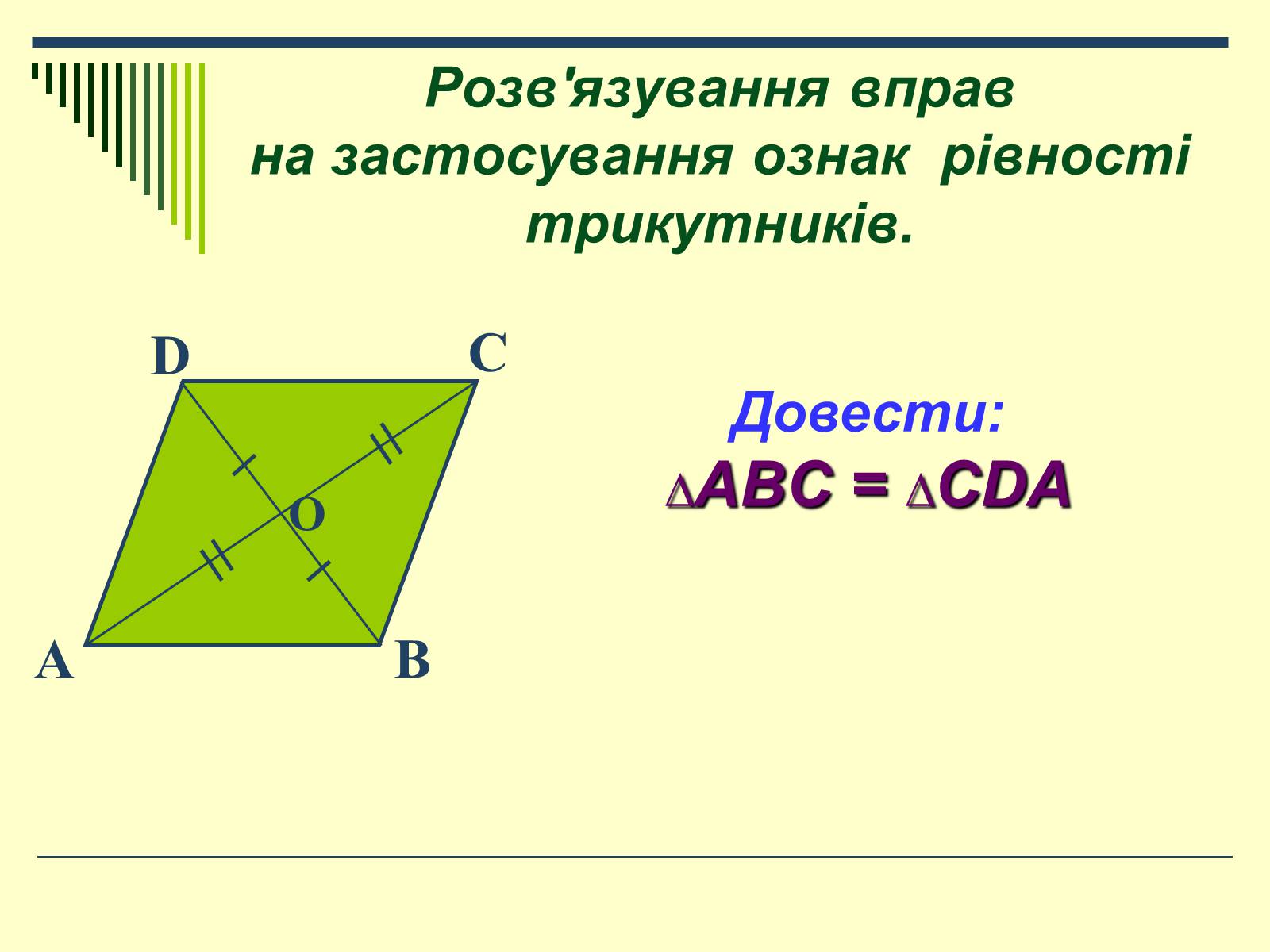
Довести:
∆ABC = ∆CDA

Розв'язування вправ на застосування ознак рівності трикутників.
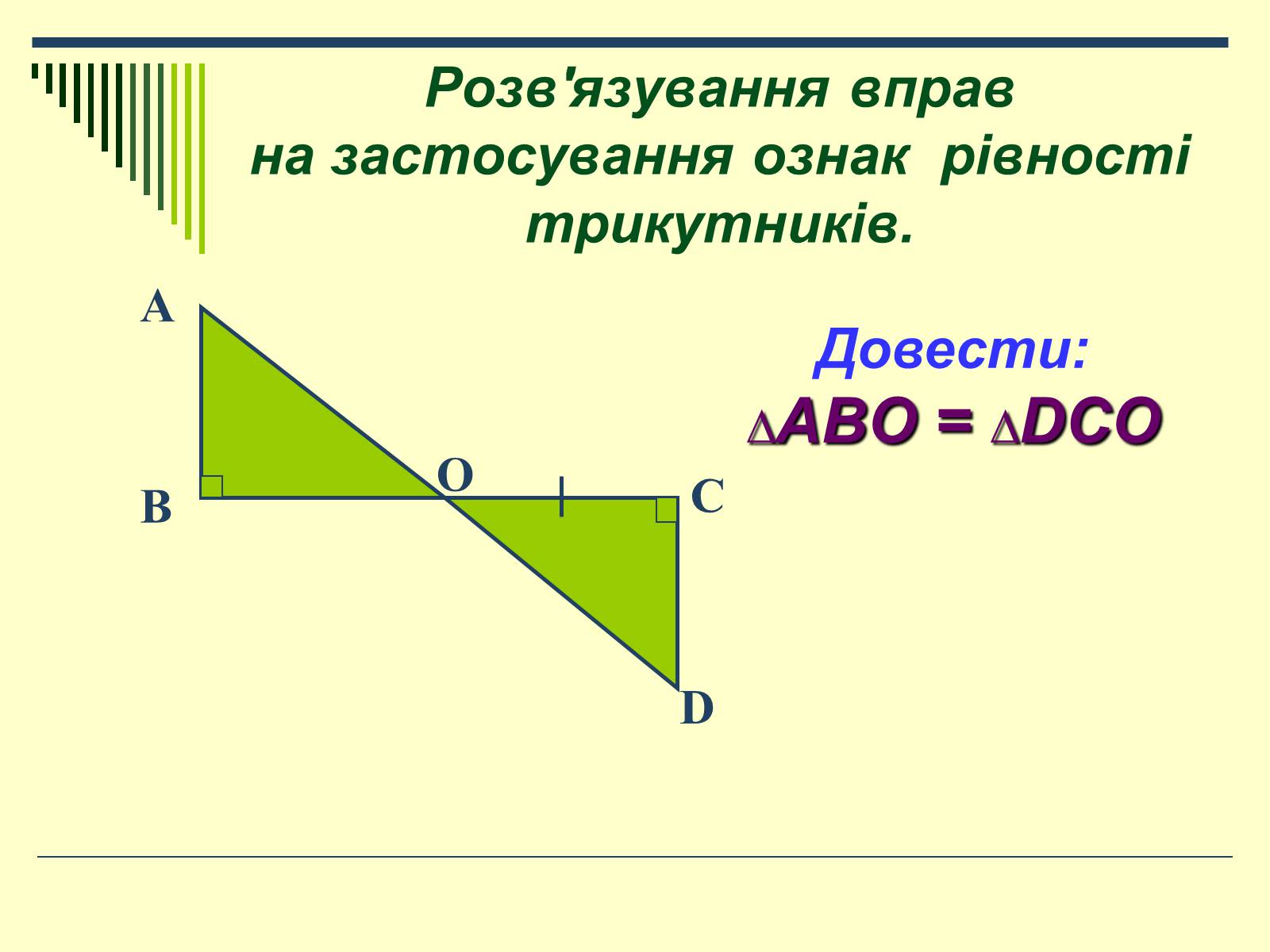
Довести:
∆ABO = ∆DCO
O
C
D
B
A

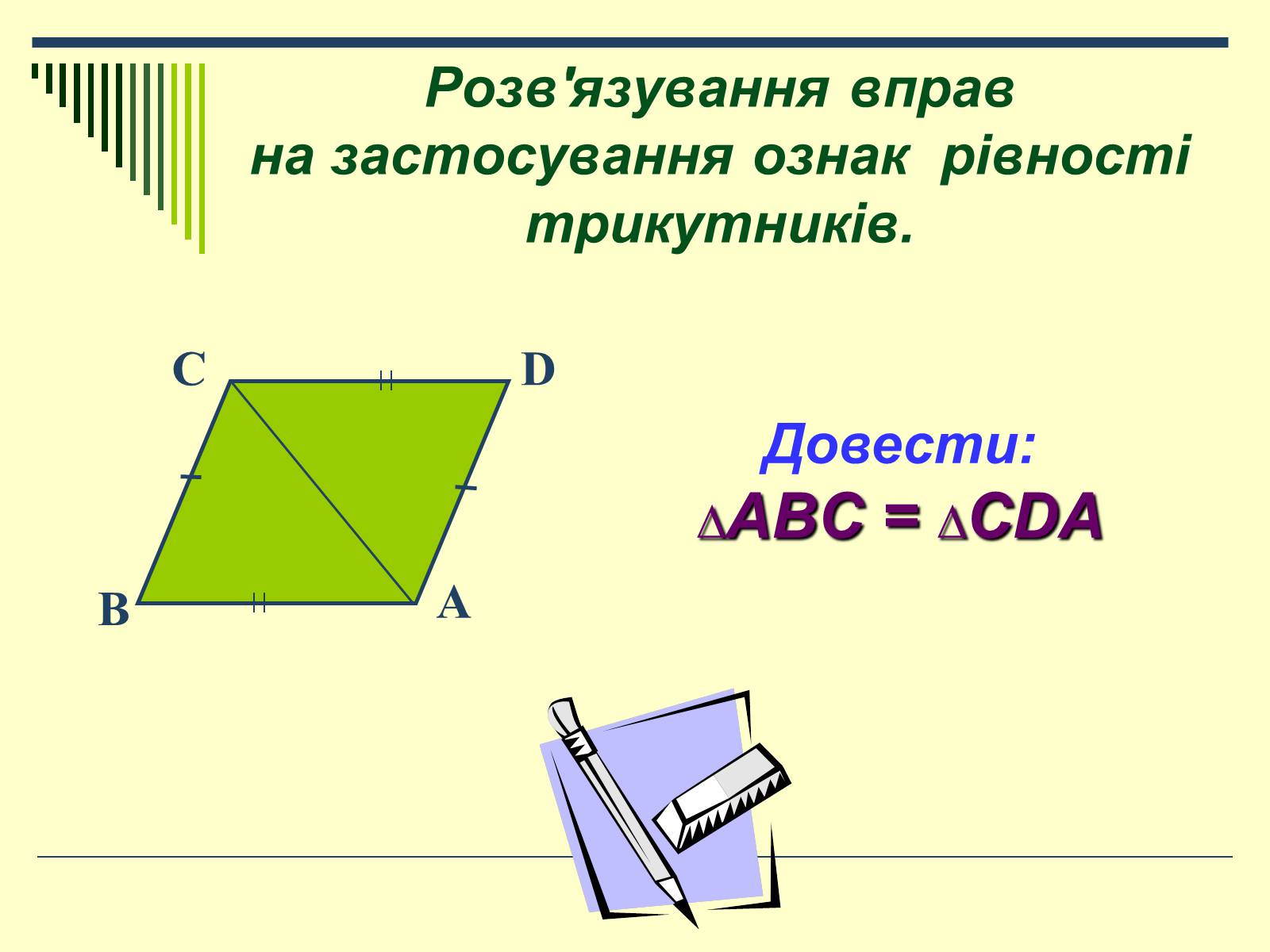
Розв'язування вправ на застосування ознак рівності трикутників.
Довести:
∆ABC = ∆CDA
B
A
D
C

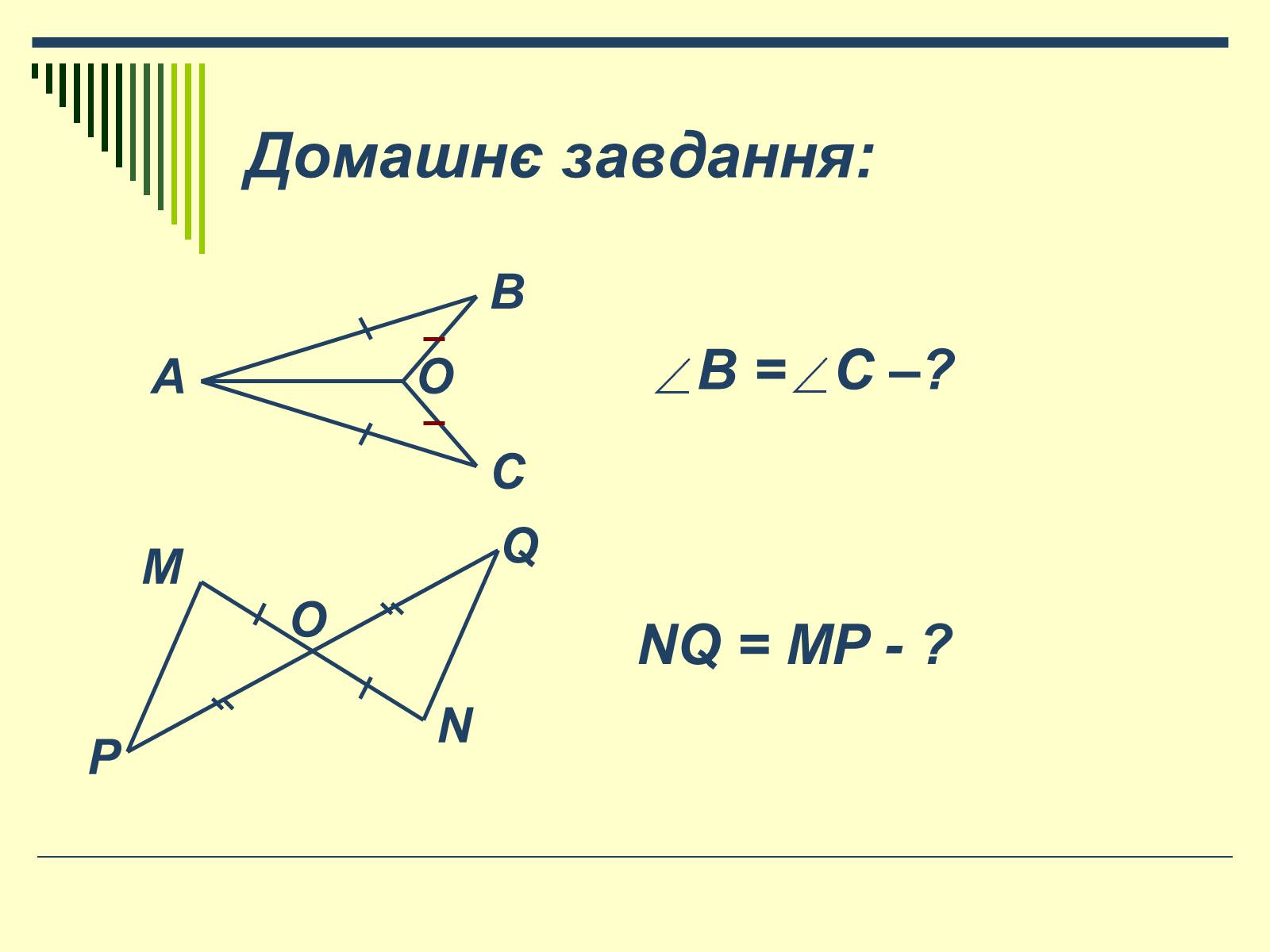
Домашнє завдання:
А
О
С
В
В = С –?
O
Q
P
M
N
NQ = MP - ?

Дякую за співпрацю ідо зустрічі !
Дякую за співпрацю ідо зустрічі !