Презентація на тему «Трапеция и её элементы»

Повторение.трапеция и её элементы
Работы ученицы 9-А класса Самойловой Катерины.

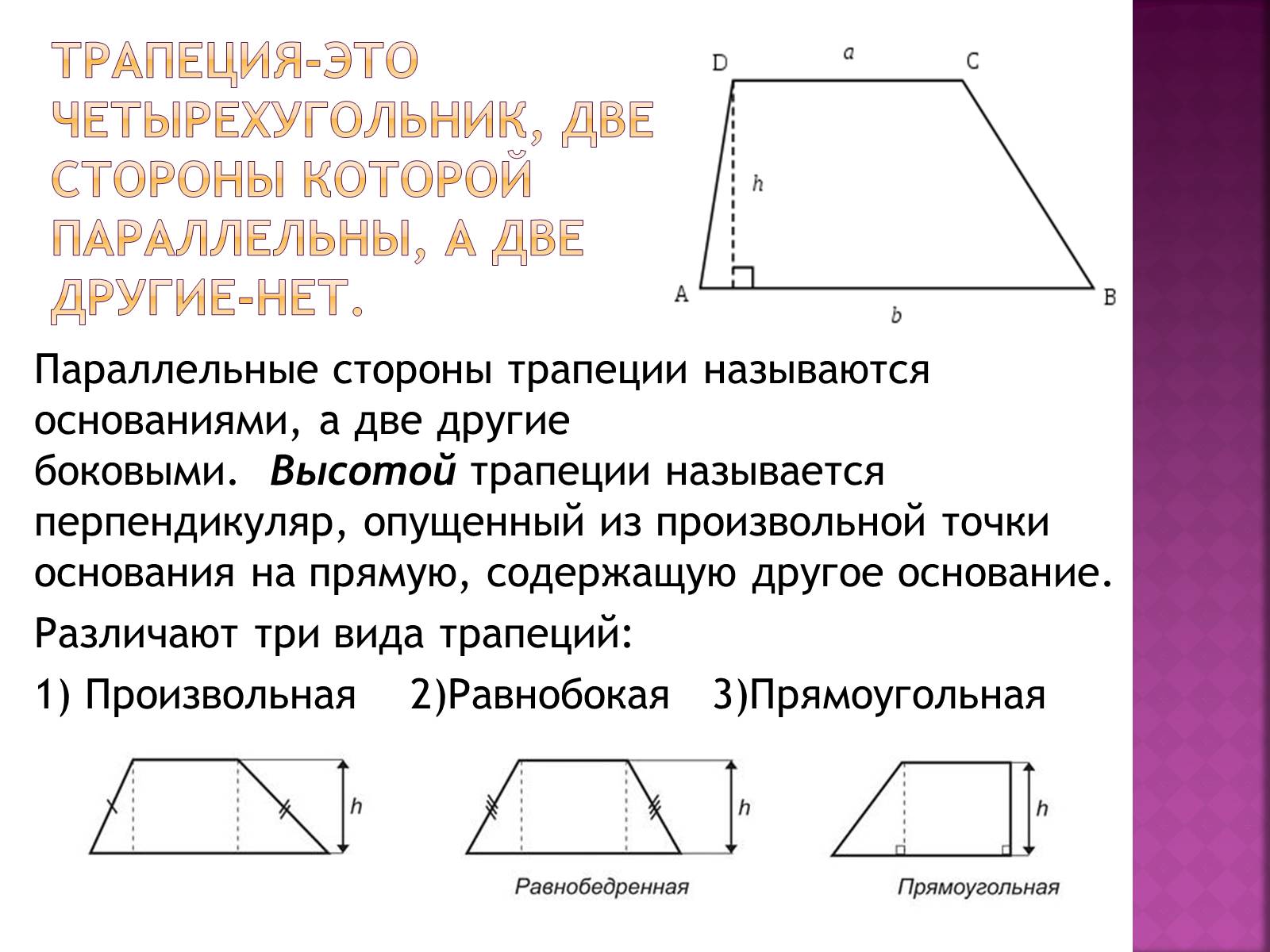
Трапеция-это четырехугольник, две стороны которой параллельны, а две другие-нет.
Параллельные стороны трапеции называются основаниями, а две другие боковыми.  Высотой трапеции называется перпендикуляр, опущенный из произвольной точки основания на прямую, содержащую другое основание.
Различают три вида трапеций:
1) Произвольная 2)Равнобокая 3)Прямоугольная

Средняя линия трапеции
Средняя линия трапеции – это отрезок, соединяющий средние точки боковых сторон треугольника.
Средняя линия трапеции равна половине его основания и параллельна ему.

Нахождение площади трапеции
Существует 4 способа нахождения площади трапеции:
1) ,где a и b-основания, а h-высота.
2) ,где d-длинна двух диагоналей и угол образованный при пересечении
3) ,где h-высота а m-длинна средней линии.
4) ,формула для равнобокой трапеции, в которую вписана окружность.

Подготовка к дпа
В-9. 2.4. В прямоугольной трапеции острый угол равен 45°. Меньшая боковая сторона и меньшее основание трапеции – по 6 см. Найдите среднюю линию трапеции.
РЕШЕНИЕ
1)Дополнительное построение: проведем
высоту CM, CM=BA=6 см.
2)Рассм. треугольник CMD-прямоугольный и
Равнобедренный, поскольку B=45, AD=AM+MD=6+6=12 см.
3)
Ответ: 9 см.

Подготовка к дпа
В-19. 2.4. В равнобедренной трапеции диагональ равно большему основанию и образует с ним угол 50º. Найдите градусную меру тупого угла трапеции.
Решение
В равнобедренном треугольнике ACD
как внутренние накрест лежащие при
Параллельных прямых AD и BC с секущей AC,
Тогда
Ответ : 115º

Подготовка к дпа
В-4. 3.3 Диагональ равнобедренной трапеции перпендикулярна к ее боковой стороне. Найдите площадь трапеции, если ее основания равны 12см и 20 см.
РЕШЕНИЕ
Пусть CK- высота трапеции. По свойству равнобе-
дреной трапеции ,тогда
AK=20-4=6 см.
Поскольку то треугольник ACD прямоугольный. Высота трапеции CK –высота треугольника ACD, проведенной к гипотенузе.
А отрезки AK и KD –проекция катетов на гипотенузу.
Следовательно , откуда CK=8 см.
Ответ:

Подготовка к дпа
В-21. 3.3. Центр окружности, описанной около трапеции, принадлежит большему основанию. Найдите углы трапеции если основании, если основания 1÷2.
РЕШЕНИЕ
По условию центр окр. – точка О – принадлежит
основанию AD трапеции. AO=DO=BO=CO как радиусы одной окружности. Поскольку по условию BC÷AD=1÷2, то
Тогда треугольник BOC равносторонний
и все углы равны по 60º. Треугольники COD и BOA равнобедренные с основаниями CD и BA соответственно.
Следовательно,
;
Ответ: 60º и 120º