Презентація на тему «Повторення курсу планіметрії»

Геометрія 10 клас
Робота
учениці 10-А класу
Баранюк Надії

ПОВТОРЕННЯКУРСУ ПЛАНІМЕТРІЇ
основні поняття планіметрії;
аксіоми – твердження, істинність яких
приймають без доведень;
основні властивості геометричних фігур
та їх ознаки;
методи розв'язування геометричних задач

ОПОРНІ ФАКТИ ПЛАНІМЕТРІЇ
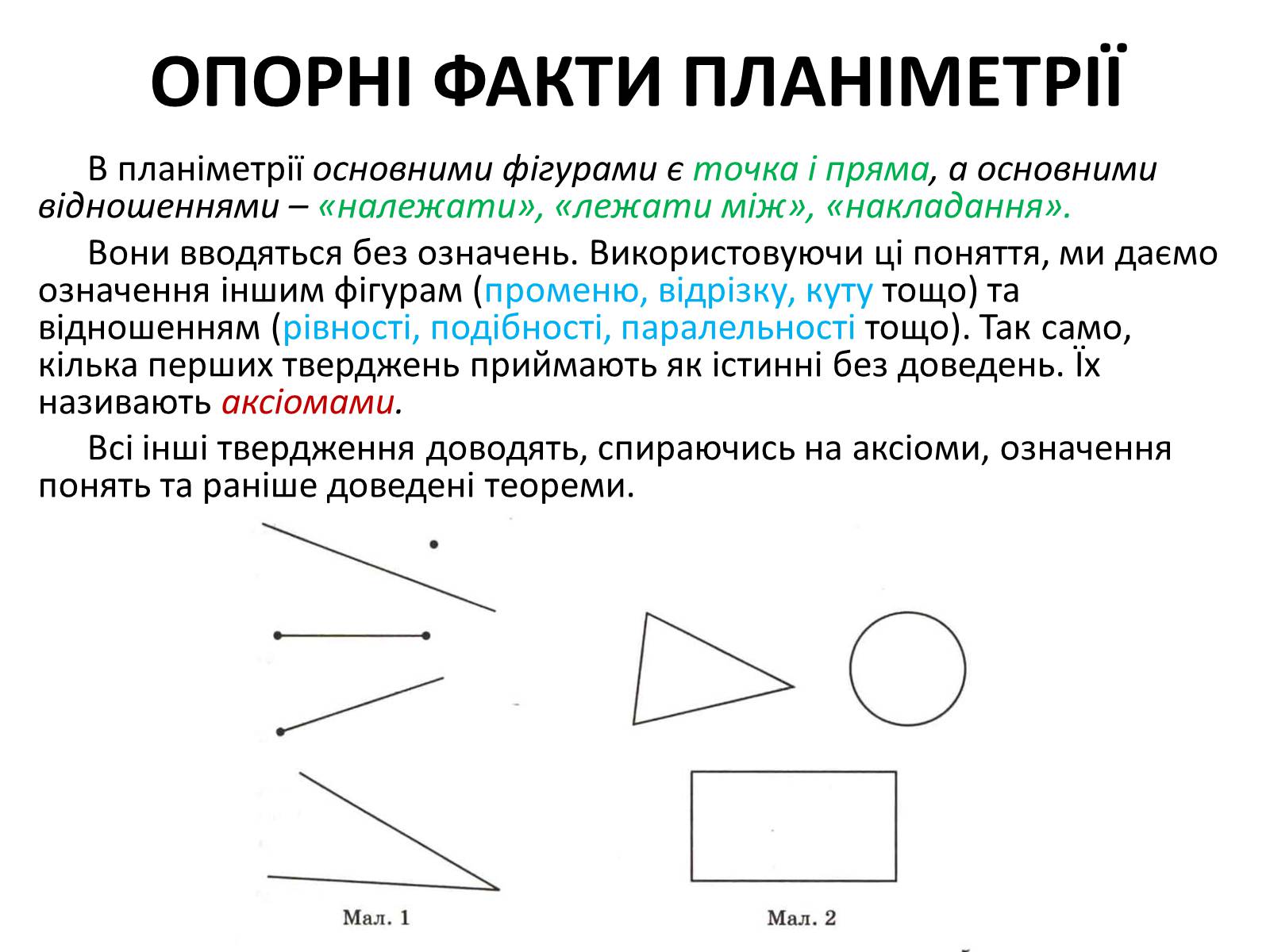
В планіметрії основними фігурами є точка і пряма, а основними відношеннями – «належати», «лежати між», «накладання».
Вони вводяться без означень. Використовуючи ці поняття, ми даємо означення іншим фігурам (променю, відрізку, куту тощо) та відношенням (рівності, подібності, паралельності тощо). Так само, кілька перших тверджень приймають як істинні без доведень. Їх називають аксіомами.
Всі інші твердження доводять, спираючись на аксіоми, означення понять та раніше доведені теореми.

ОПОРНІ ФАКТИ ПЛАНІМЕТРІЇ
В планіметрії основними фігурами є точка і пряма, а основними відношеннями – «належати», «лежати між», «накладання».
Вони вводяться без означень. Використовуючи ці поняття, ми даємо означення іншим фігурам (променю, відрізку, куту тощо) та відношенням (рівності, подібності, паралельності тощо). Так само, кілька перших тверджень приймають як істинні без доведень. Їх називають аксіомами.
Всі інші твердження доводять, спираючись на аксіоми, означення понять та раніше доведені теореми.

ОПОРНІ ФАКТИ ПЛАНІМЕТРІЇ
В планіметрії основними фігурами є точка і пряма, а основними відношеннями – «належати», «лежати між», «накладання».
Вони вводяться без означень. Використовуючи ці поняття, ми даємо означення іншим фігурам (променю, відрізку, куту тощо) та відношенням (рівності, подібності, паралельності тощо). Так само, кілька перших тверджень приймають як істинні без доведень. Їх називають аксіомами.
Всі інші твердження доводять, спираючись на аксіоми, означення понять та раніше доведені теореми.

Кути
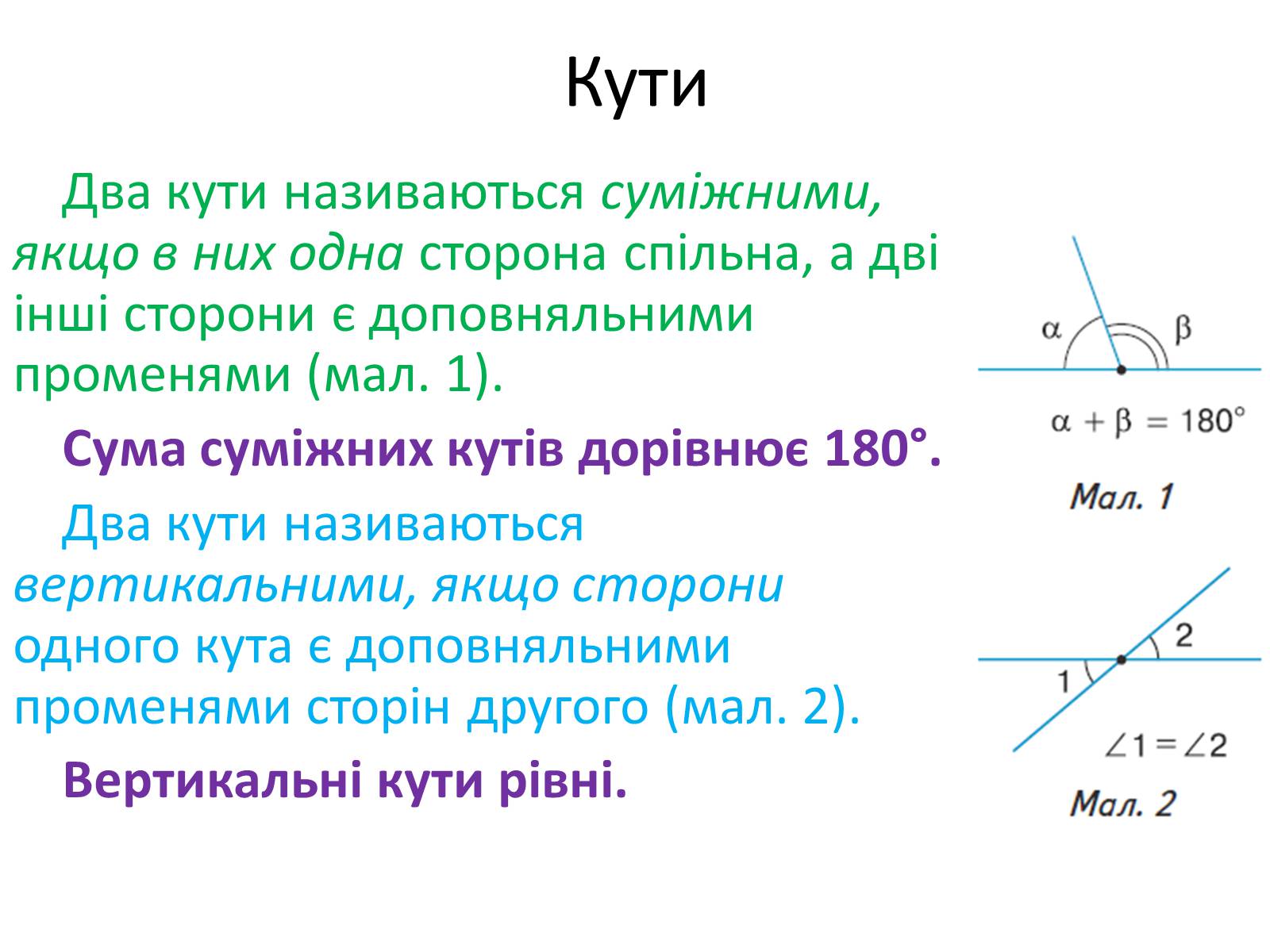
Два кути називаються суміжними, якщо в них одна сторона спільна, а дві інші сторони є доповняльними променями (мал. 1).
Сума суміжних кутів дорівнює 180°.
Два кути називаються вертикальними, якщо сторони одного кута є доповняльними променями сторін другого (мал. 2).
Вертикальні кути рівні.

Властивості паралельних прямих
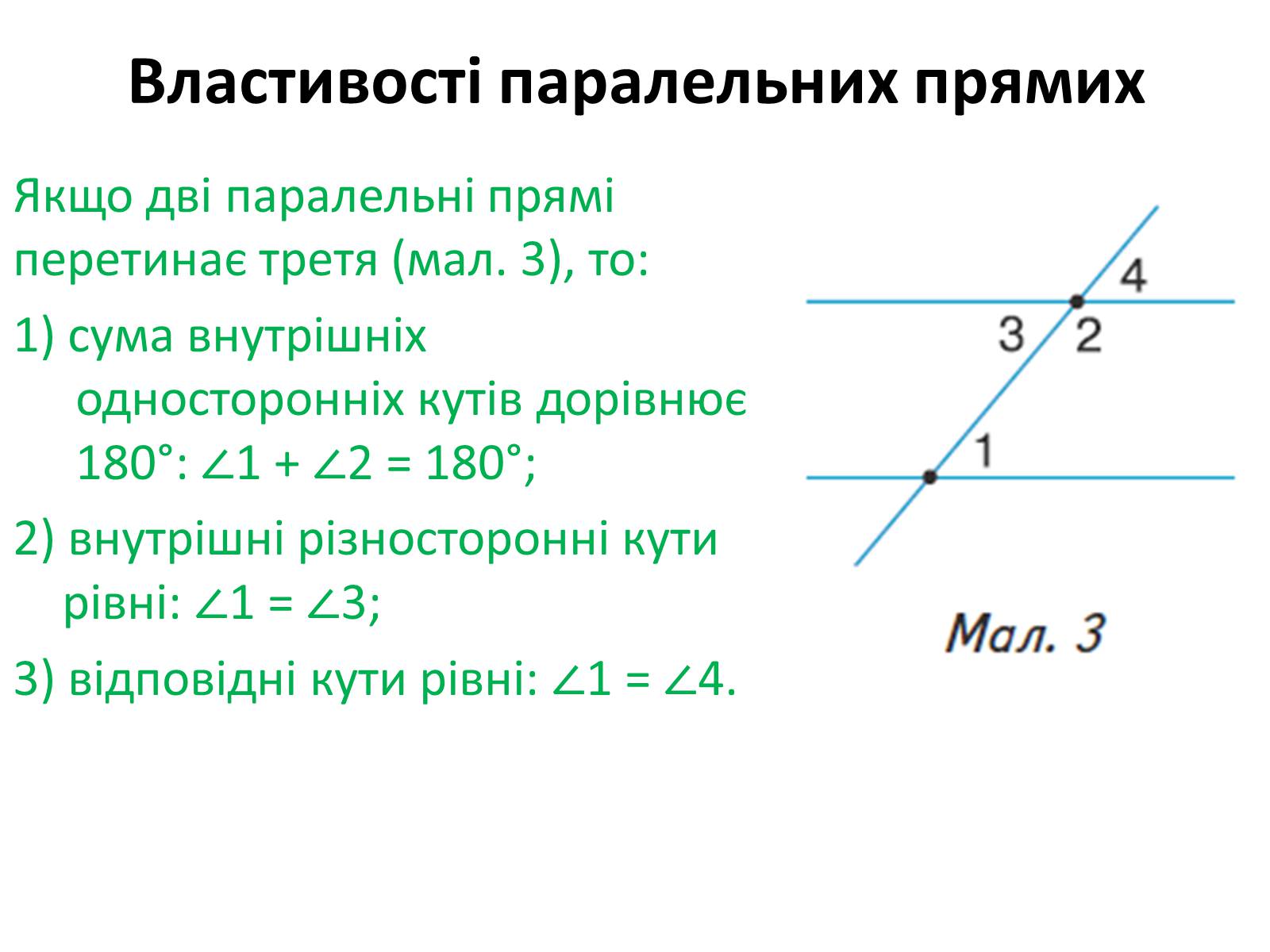
Якщо дві паралельні прямі перетинає третя (мал. 3), то:
1) сума внутрішніх односторонніх кутів дорівнює 180°: ∠1 + ∠2 = 180°;
2) внутрішні різносторонні кути рівні: ∠1 = ∠3;
3) відповідні кути рівні: ∠1 = ∠4.

Трикутники
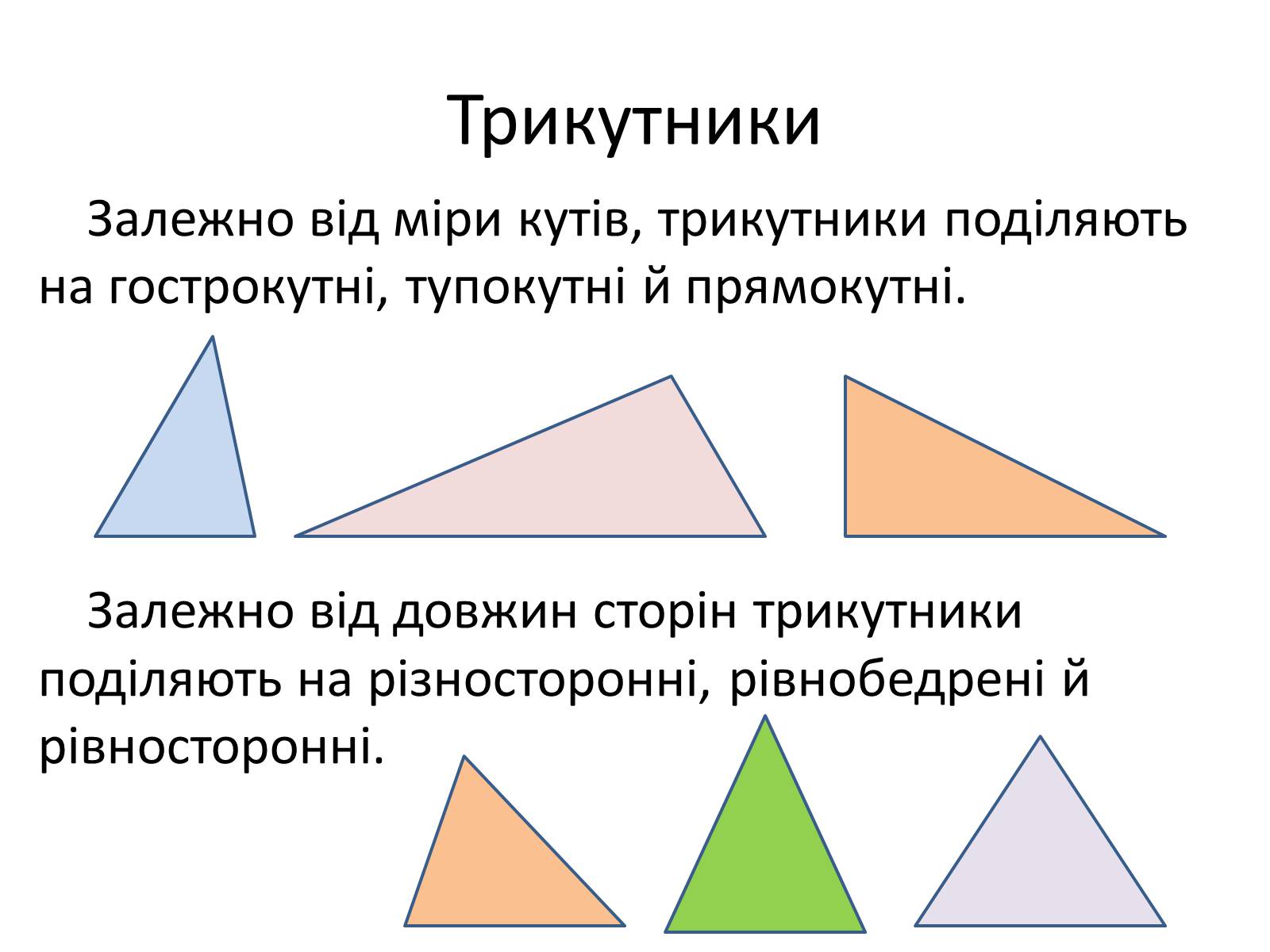
Залежно від міри кутів, трикутники поділяють на гострокутні, тупокутні й прямокутні.
Залежно від довжин сторін трикутники поділяють на різносторонні, рівнобедрені й рівносторонні.

Трикутники

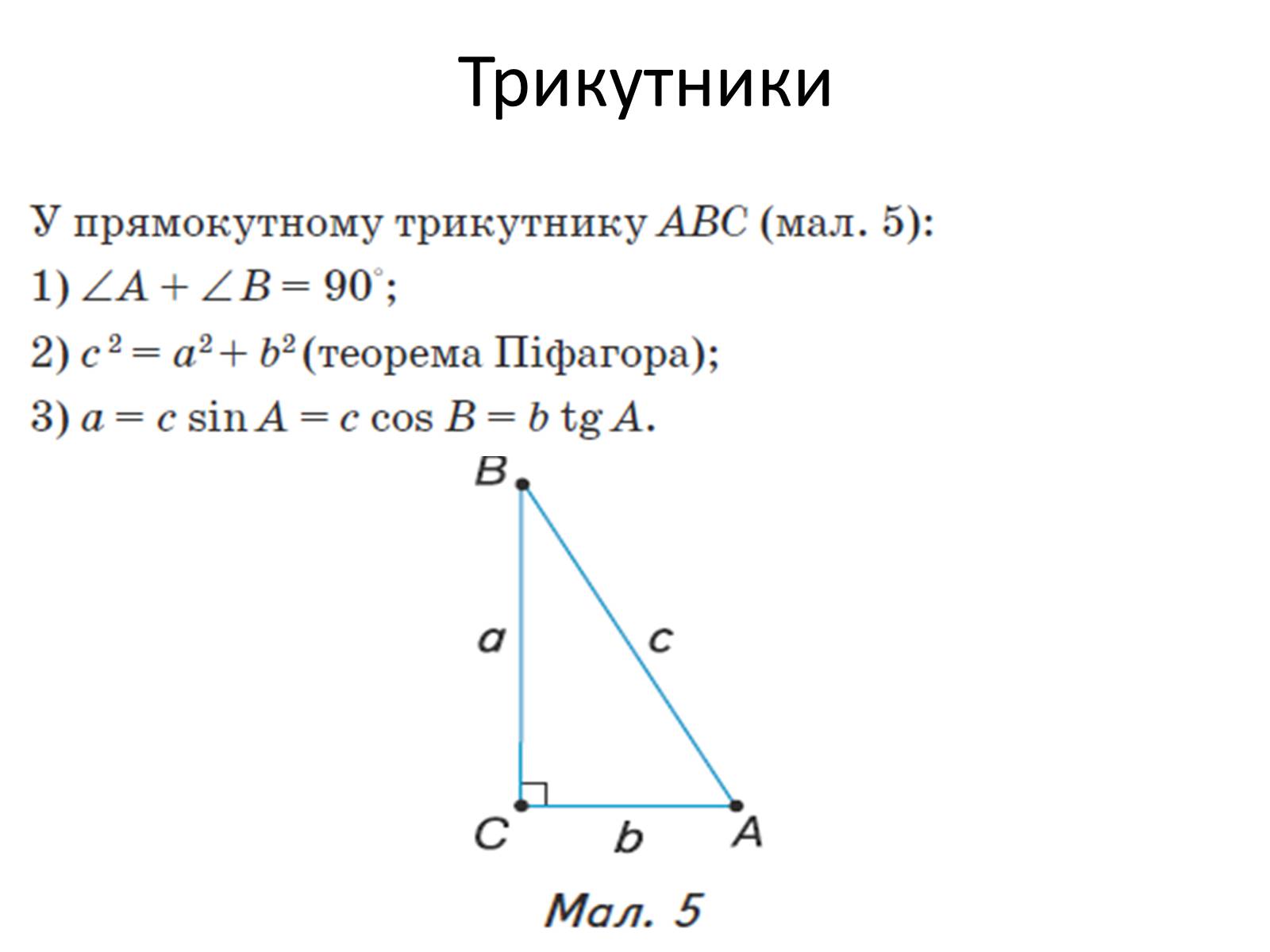
Трикутники

Трикутник

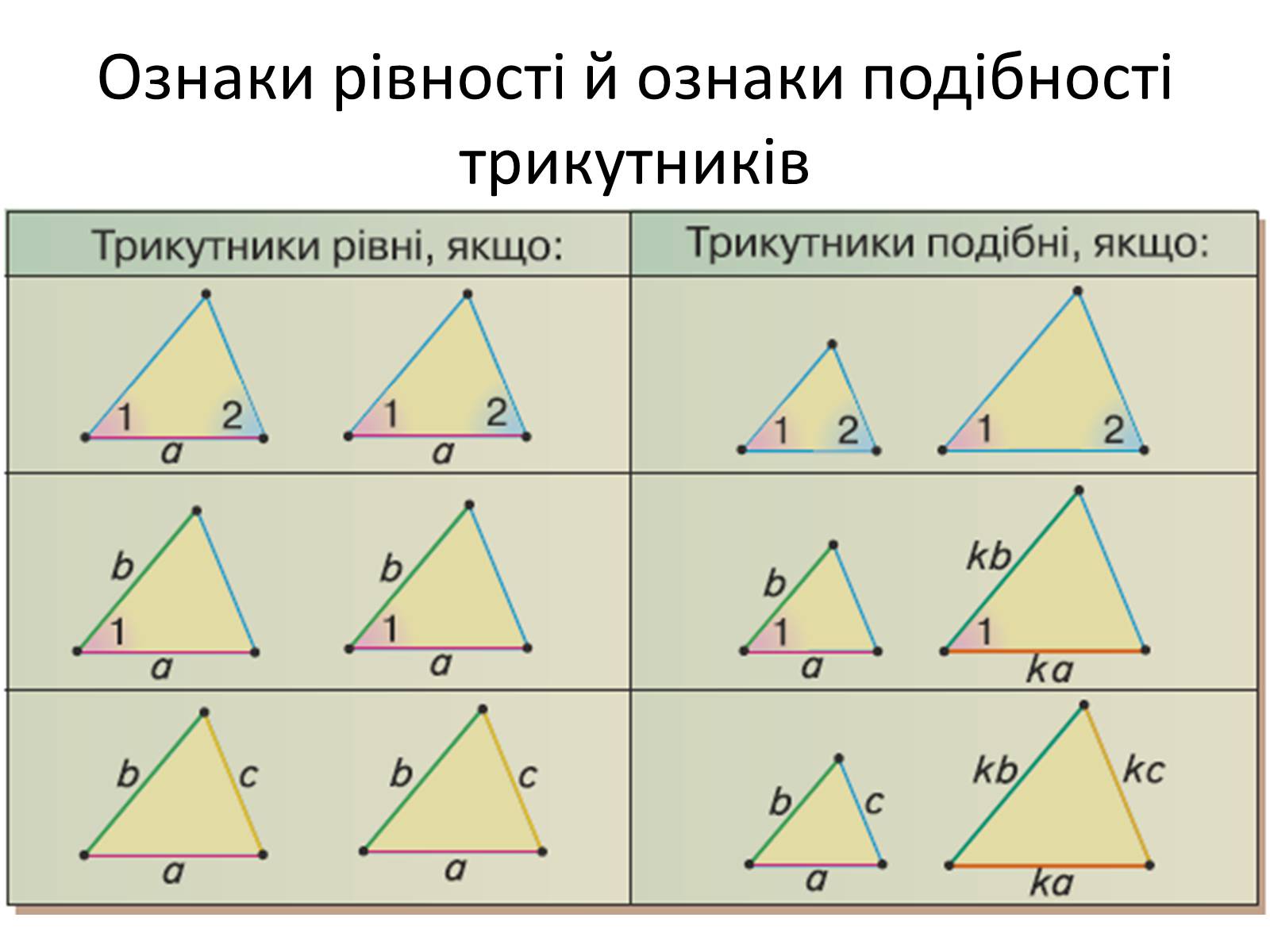
Ознаки рівності й ознаки подібності трикутників

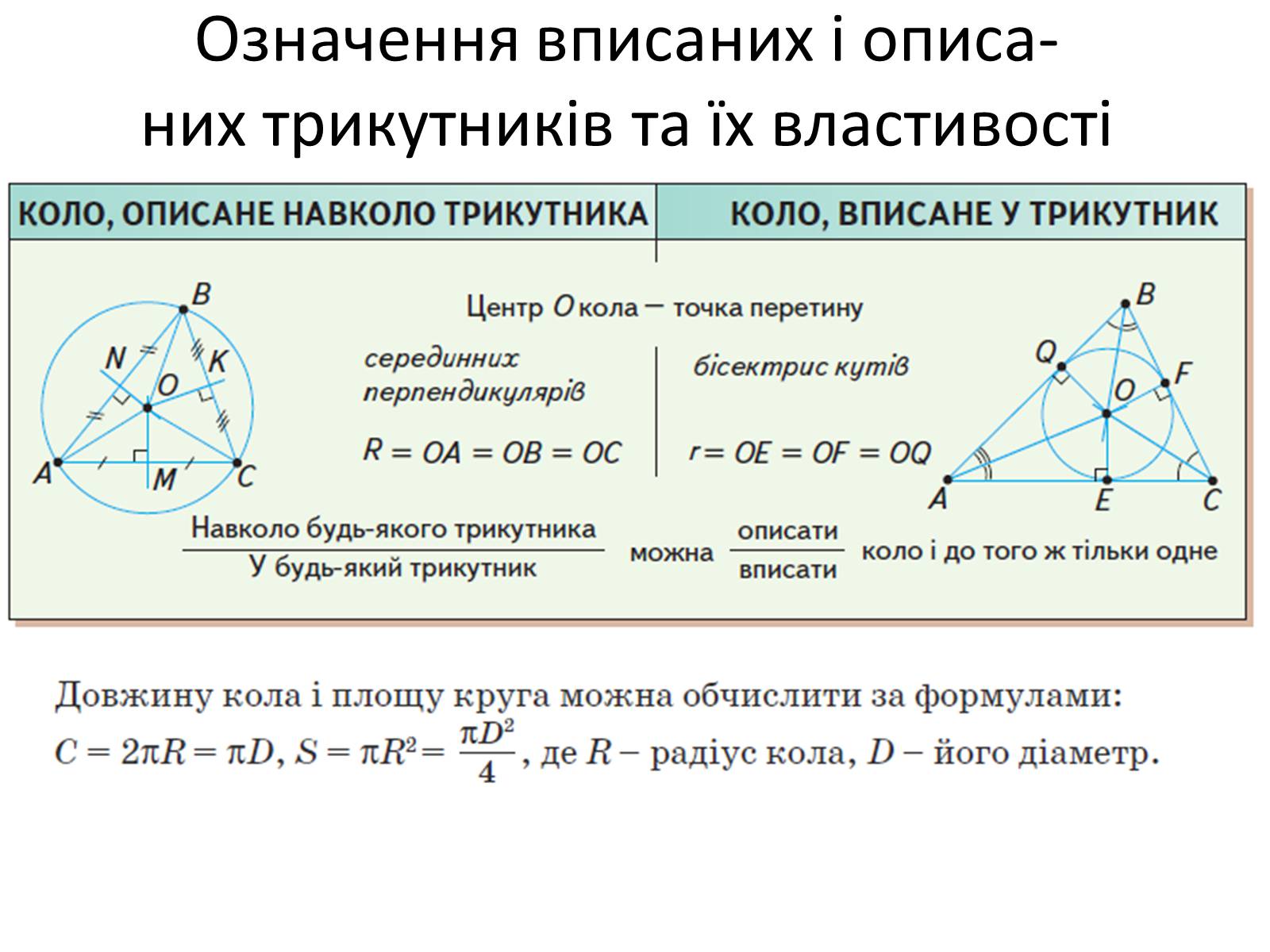
Означення вписаних і описа-них трикутників та їх властивості

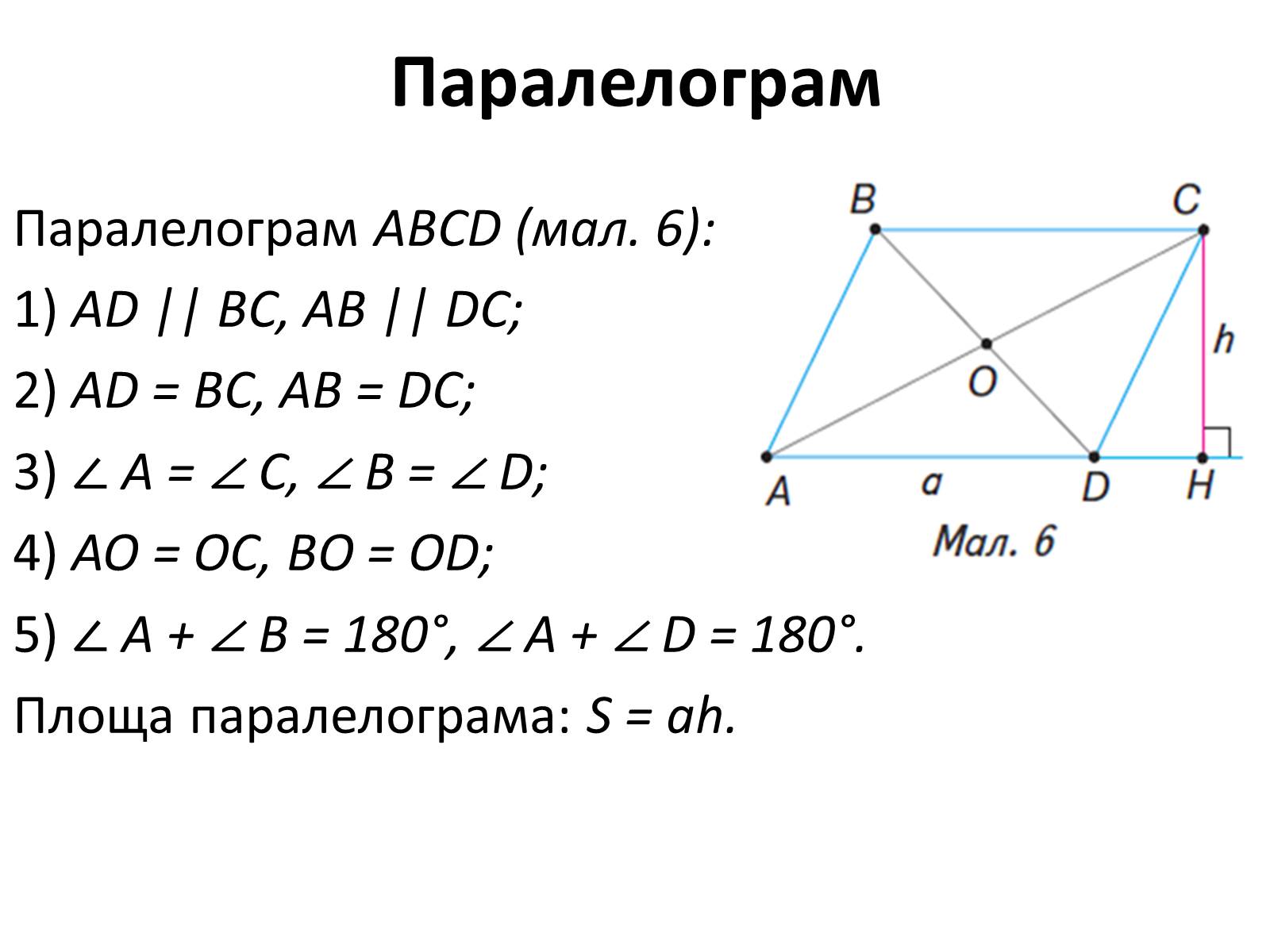
Паралелограм
Паралелограм ABCD (мал. 6):
1) AD || BC, AB || DC;
2) AD = BC, AB = DC;
3) ∠ A = ∠ C, ∠ B = ∠ D;
4) AO = OC, BO = OD;
5) ∠ A + ∠ B = 180°, ∠ A + ∠ D = 180°.
Площа паралелограма: S = ah.

Прямокутник
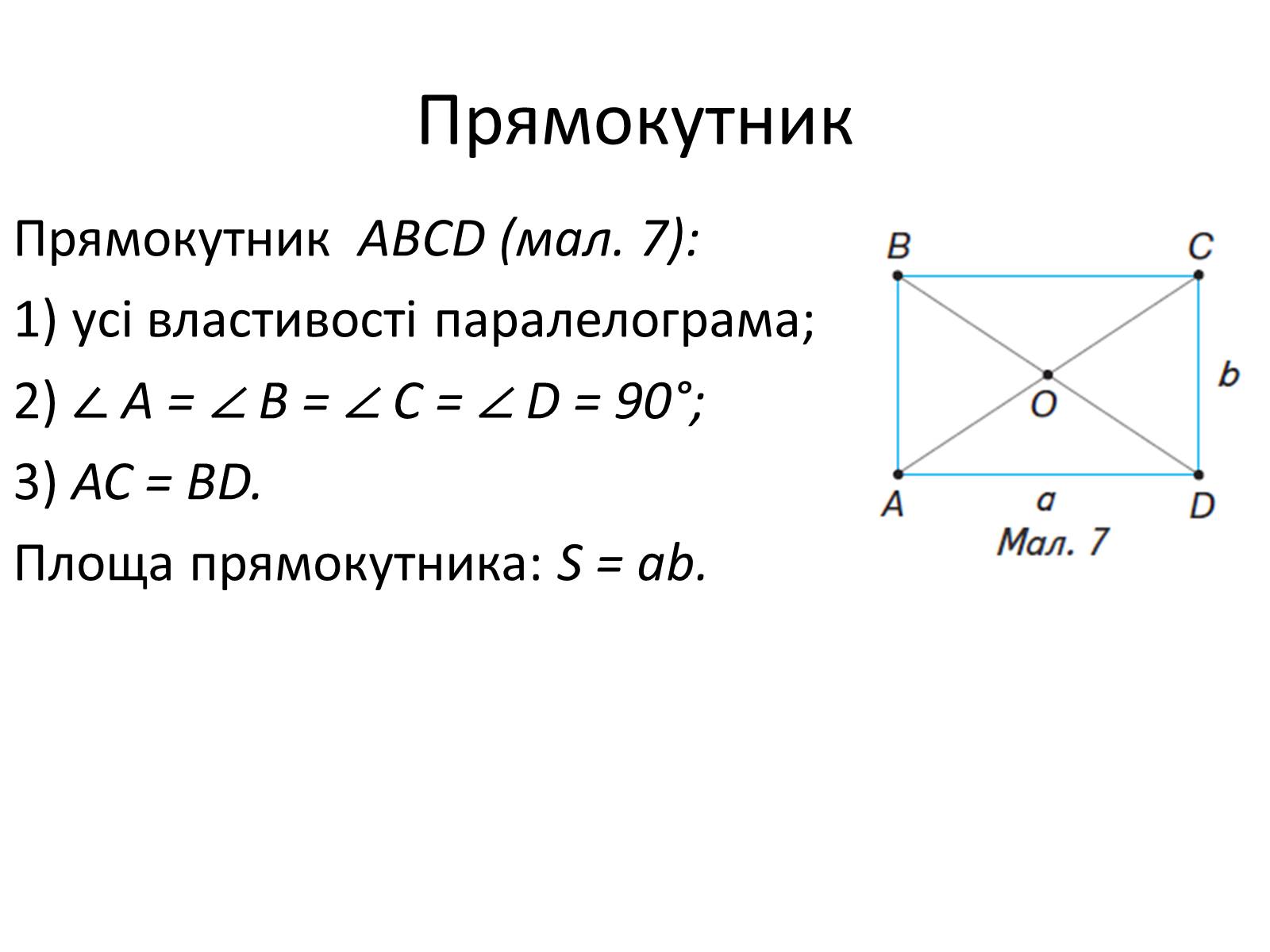
Прямокутник ABCD (мал. 7):
1) усі властивості паралелограма;
2) ∠ A = ∠ В = ∠ С = ∠ D = 90°;
3) АС = ВD.
Площа прямокутника: S = ab.

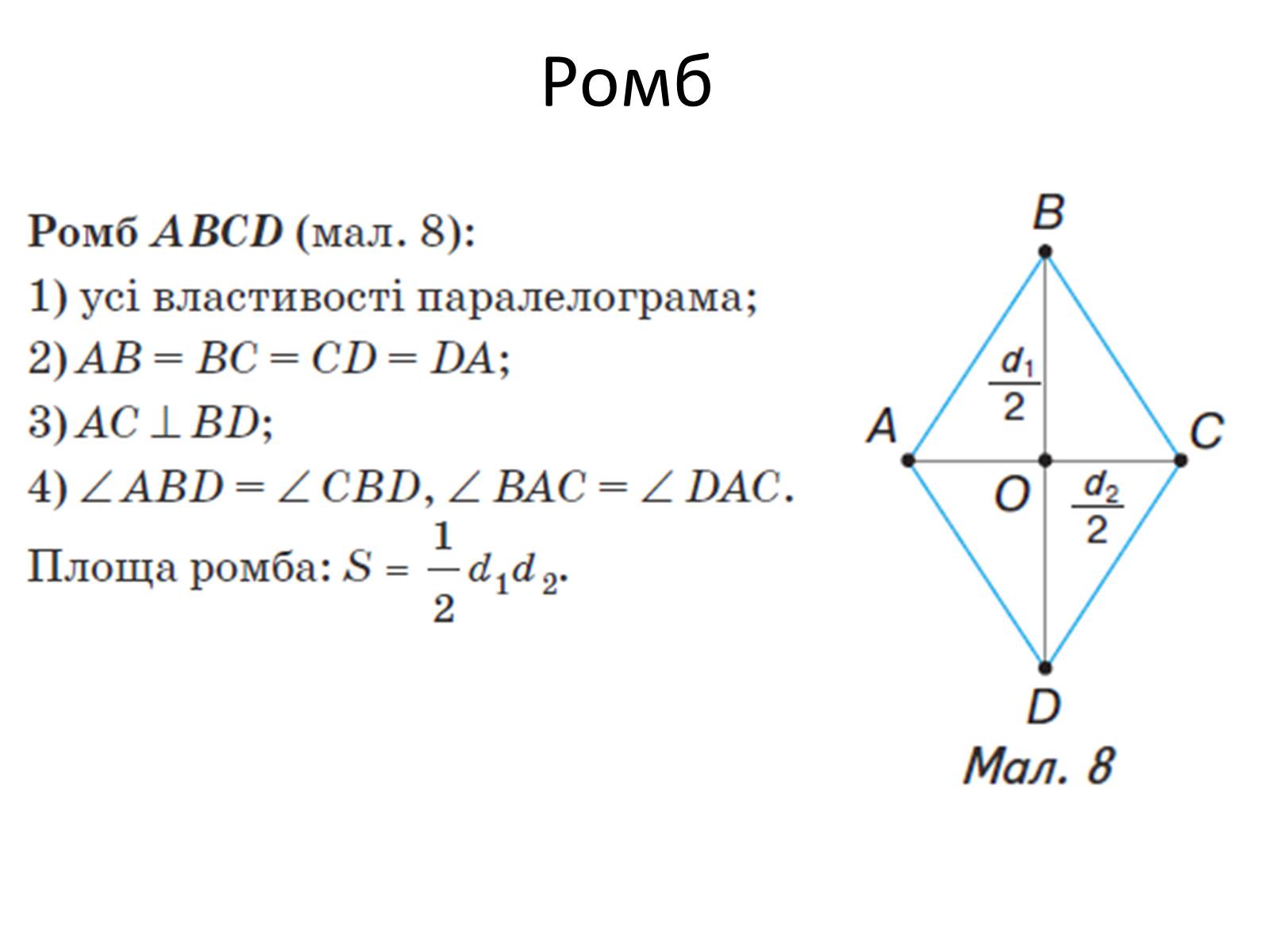
Ромб

Квадрат
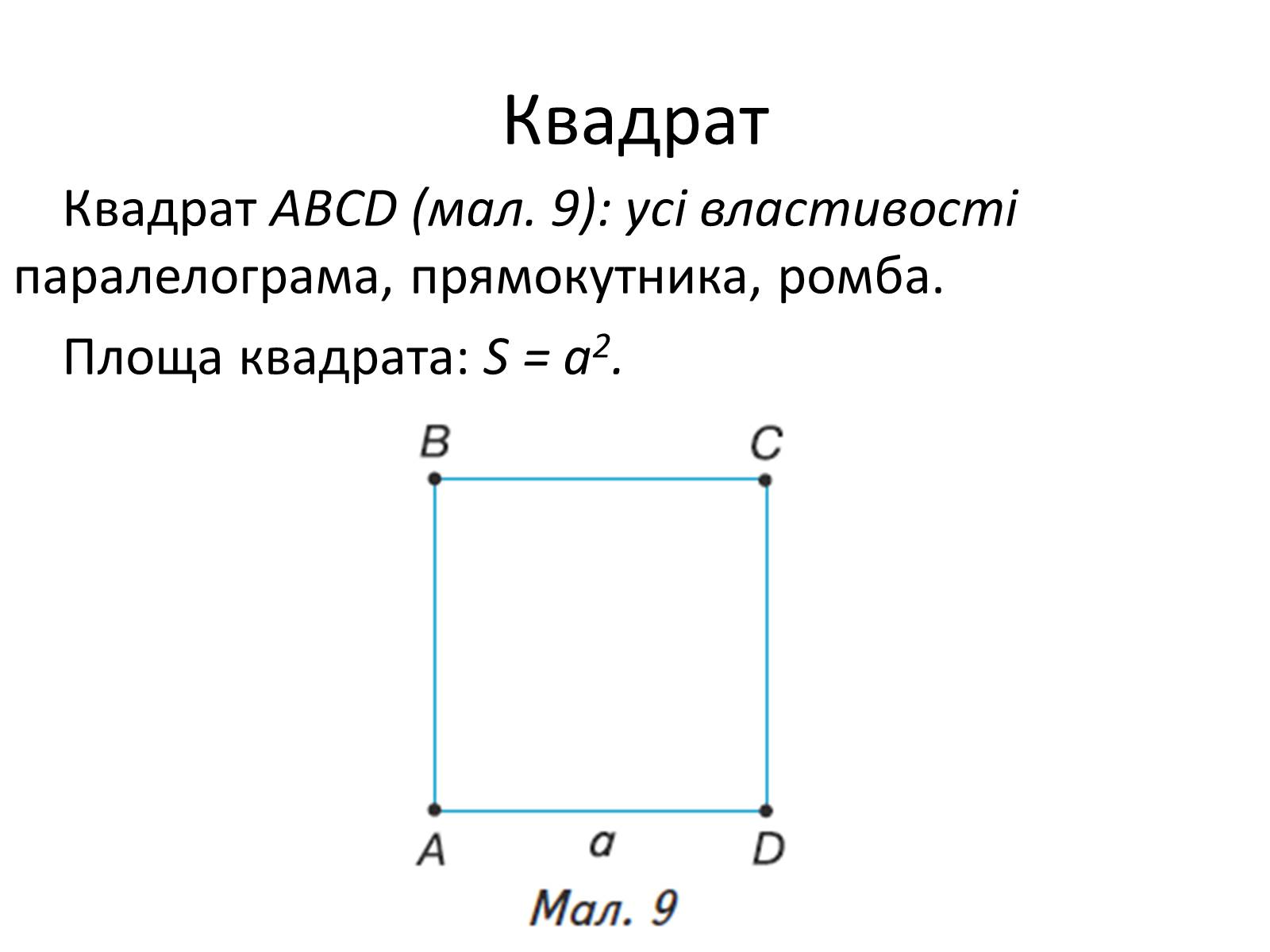
Квадрат ABCD (мал. 9): усі властивості паралелограма, прямокутника, ромба.
Площа квадрата: S = a2.

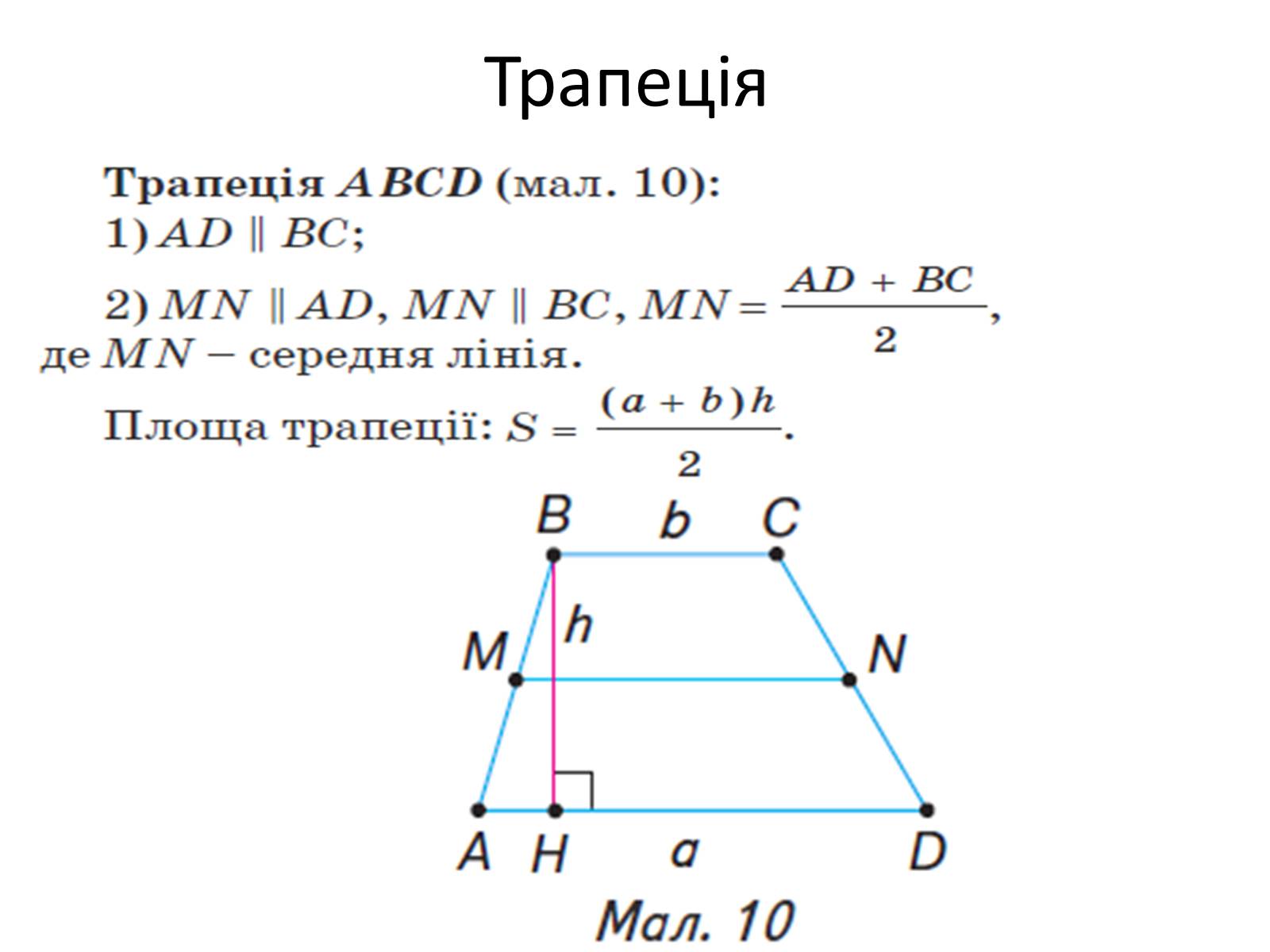
Трапеція

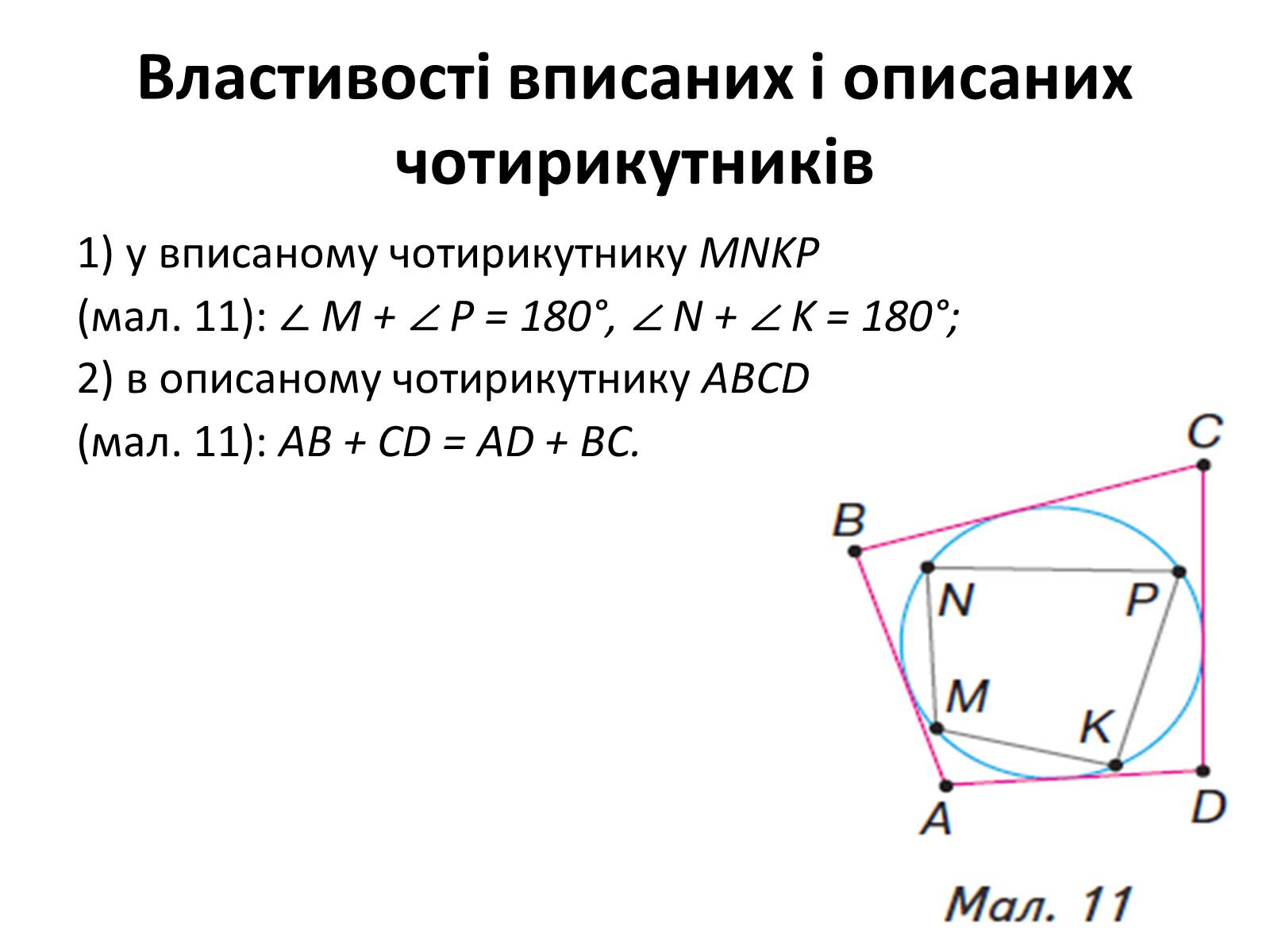
Властивості вписаних і описанихчотирикутників
1) у вписаному чотирикутнику MNKP
(мал. 11): ∠ M + ∠ P = 180°, ∠ N + ∠ K = 180°;
2) в описаному чотирикутнику ABCD
(мал. 11): AB + CD = AD + BC.

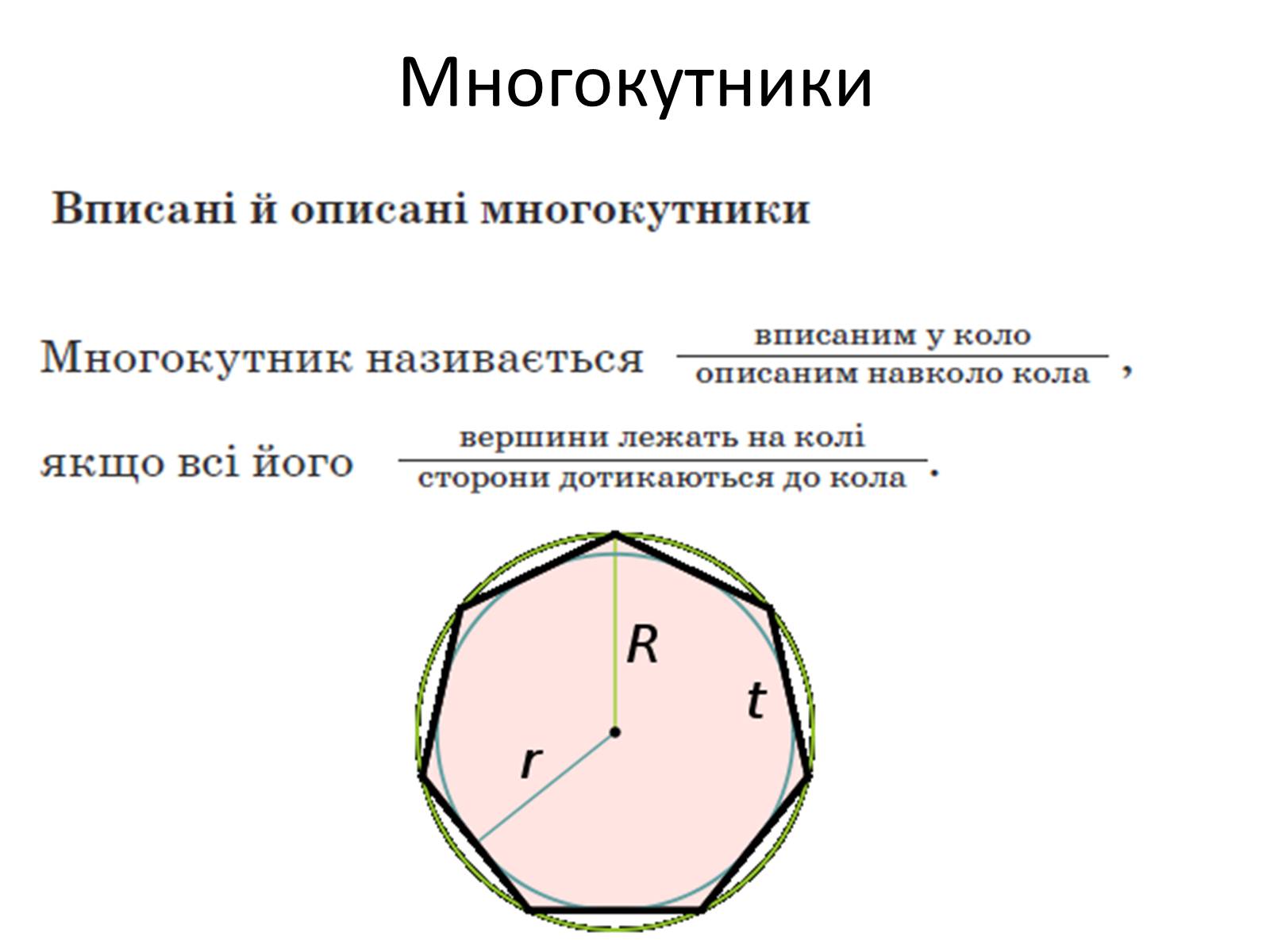
Многокутники

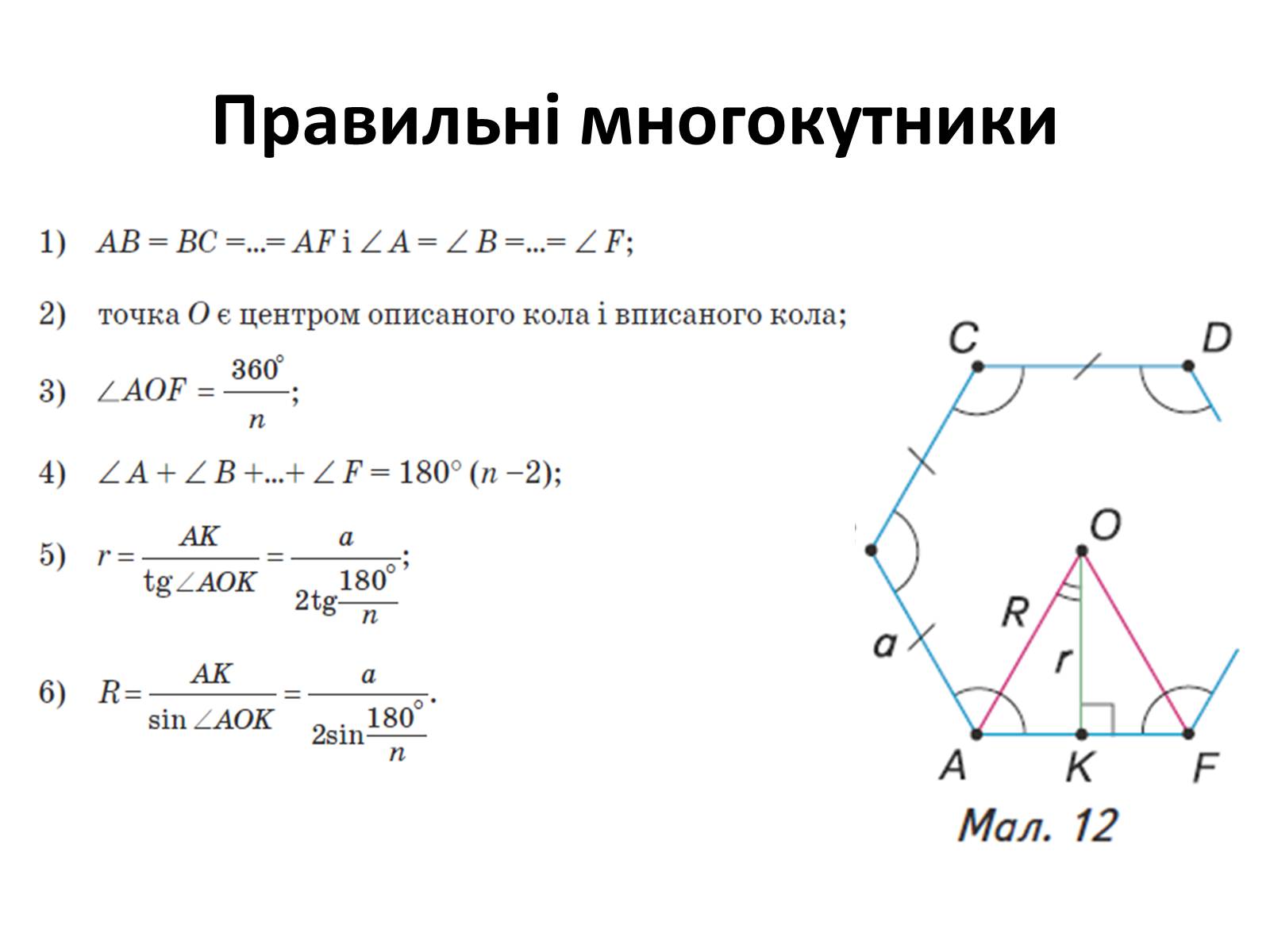
Правильні многокутники