Презентація на тему «Показникові рівняння та нерівності»

Показникові рівняння та нерівності. Основні види та способи їх розв'язування.

Показникові рівняння
Найпростіші показникові рівняння.
Рівняння в яких ліву і праву частину зводять до показників з однаковими основами.
Заміна змінної в показникових рівняннях.

①Найпростіші показникові рівняння
=bt→
 
 
Наприклад:
3
Відповідь:
 

②Рівняння в яких ліву і праву частину зводять до показників з однаковими основами
 

③Заміна змінної в показникових рівняннях
Розв'язання
Заміна:, тоді
 
Повертаючись до заміни, маємо:
Відповідь:-2.
 

Однорідні показникові рівняння та рівняння, що зводяться до однорідних

Рівняння виду:
…
…
Де
деякі числа.
 

Наприклад:
 

Спосіб розвязання
Щоб розв'язати однорідні рівняння потрібно праву і ліву частину рівняння поділити на
Наприклад:
Розв'язання
 

Заміна:
Повертаючись до заміни, маємо:
│ │
Відповідь: 0; 1.
 

Розв'язання
Заміна:
 
Рівняння, що зводиться до однорідних
Повертаючись до заміни, маємо:
Відповідь: 0; 1.
 

Заміна: =t
 
=0
Розв'язання
 
Повертаючись до заміни, маємо:
 

2x-1
 

Показникові рівняння типу:
де
Розв'язання
Так як то
Робимо заміну: тоді
 

Наприклад:
Розв'язання
Заміна: , тоді
Повертаючись до заміни, маємо:
│
Відповідь: -1; 1.
 

Przyklad w zeszycie
І далі 3 слайди, в яких я не можу розібратися(

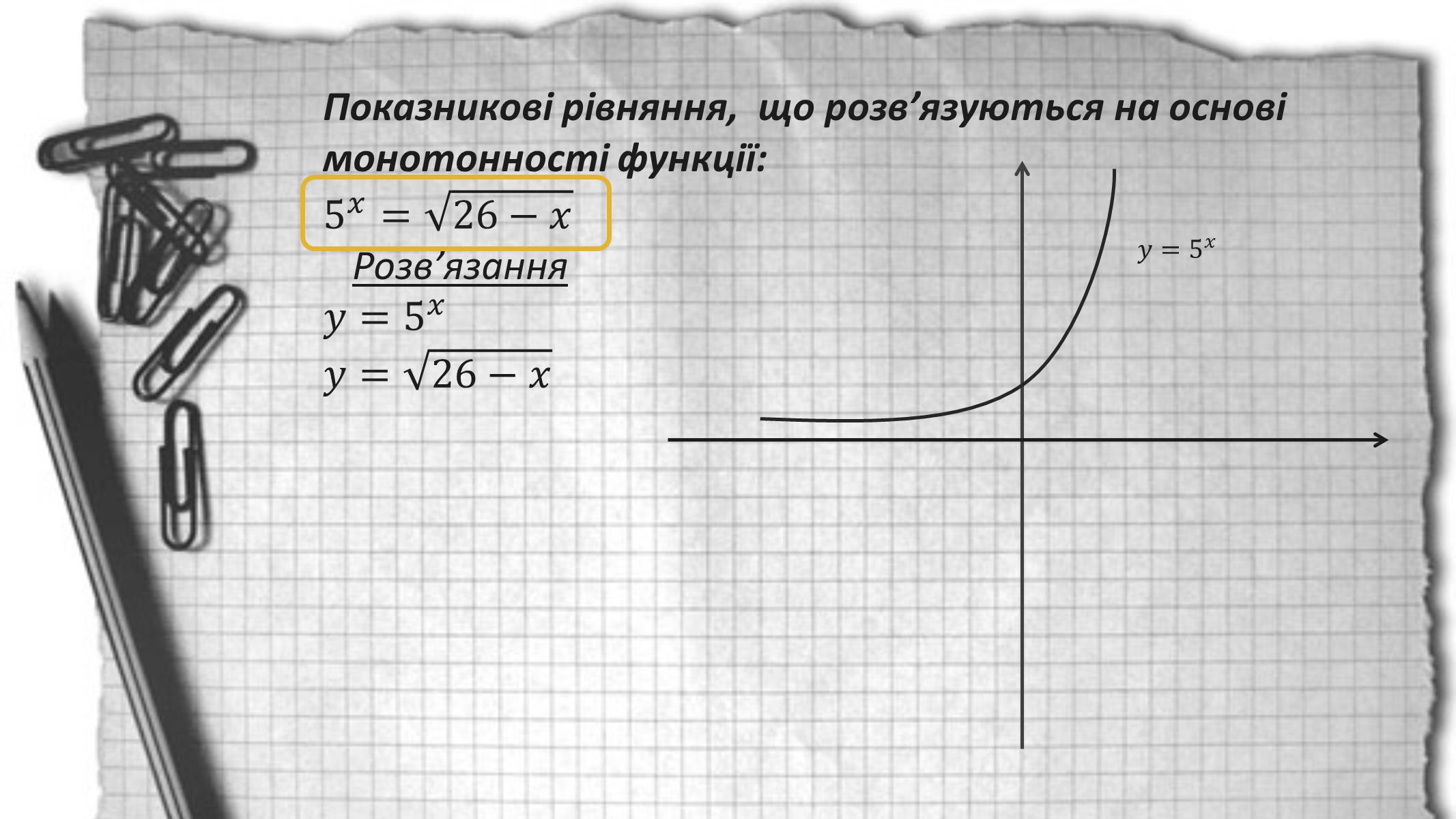
Показникові рівняння, що розв'язуються на основі монотонності функції:
Розв'язання
 
 

Висновок:
1)Функція монотонно зростає на всій області визначення ;
2) монотонно спадає на всій області визначення;
Тому їх графіки можуть перетнутись тільки в одній точці Х=1 - корінь рівняння
 

Заміна:
Повертаючись до заміни, маємо:
(1):
Х=1 – корінь рівнянняі він єдиний , бо - метод зростає на всій осі D(f), а ф-я y=5-x - монотонно спадає в D(f), тому їх графіки можуть мати єдину спільну точку
Відповідь: 1
 

Показникові нерівності

① Найпростіші
1.
Розв'язання
Відповідь:
 
2
x
2.
Розв'язання
Прирівнюємо до нуля:
Відповідь: (-2; -1).
 
-2
-1
x
Якщо основа степеня <1, то знак розвертається!

② Заміна змінної
1)
Розв'язання
Заміна:
0Повертаючись до заміни, маємо:
0<
 
 
 
 
x
t
t
-6
6

③ Однорідні нерівності
Розв'язання
Заміна :
Прирівнюємо до нуля:
 
Повертаючись до заміни, маємо:
│
Відповідь:
 

④ Окремі типи
Розв'язання
Відповідь: (-∞; 2).
 

Розв'язання
Поділимо ліву і праву частини на
Відповідь: ( 0; +∞).
 

⑤ Нерівності, що розв'язуються графічним способом
Розв'язання
Побудуємо графіки
функцій
-1
 

Розв'язання
Побудуємо графіки
функцій