Презентація на тему «Ознаки паралельності прямих»

Ознаки паралельності прямих
Пояснення відмінності означення і ознаки, доведення ознак паралельності прямих, розв'язування тренувальних вправи.
Вчитель математики Березанської ЗОШ Алексєєнко В.І.

Означення паралельних прямих
Дві прямі в просторі називаються паралельними, якщо вони лежать в одній площині і не перетинаються.
Для того, щоб на практиці з'ясовувати паралельність прямих, недостатньо знати означення паралельних прямих Тому ми доведемо певні твердження, які називаються ознакою паралельності прямих
Ознака і означення є різні речі, тому їх не слід плутати.
Означення говорить про те, що таке означуване поняття, описує його,
ознака – це властивість цього ж поняття, яку часто застосовують на практиці, і яка найчастіше є теоремою.
Є три ознаки паралельності прямих
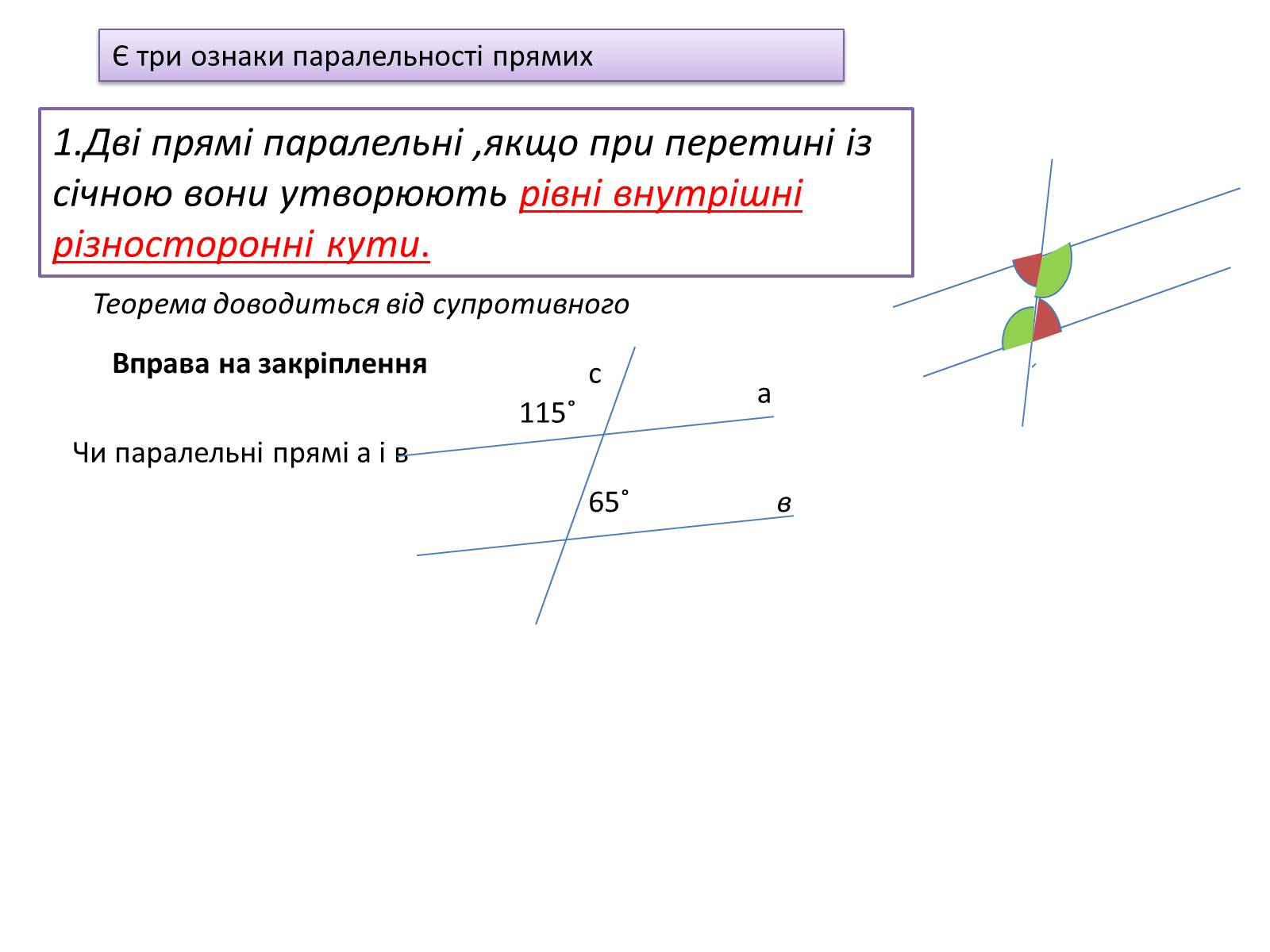
1.Дві прямі паралельні ,якщо при перетині із січною вони утворюють рівні внутрішні різносторонні кути.
Теорема доводиться від супротивного
Чи паралельні прямі а і в
а
в
с
65˚
115˚
Вправа на закріплення
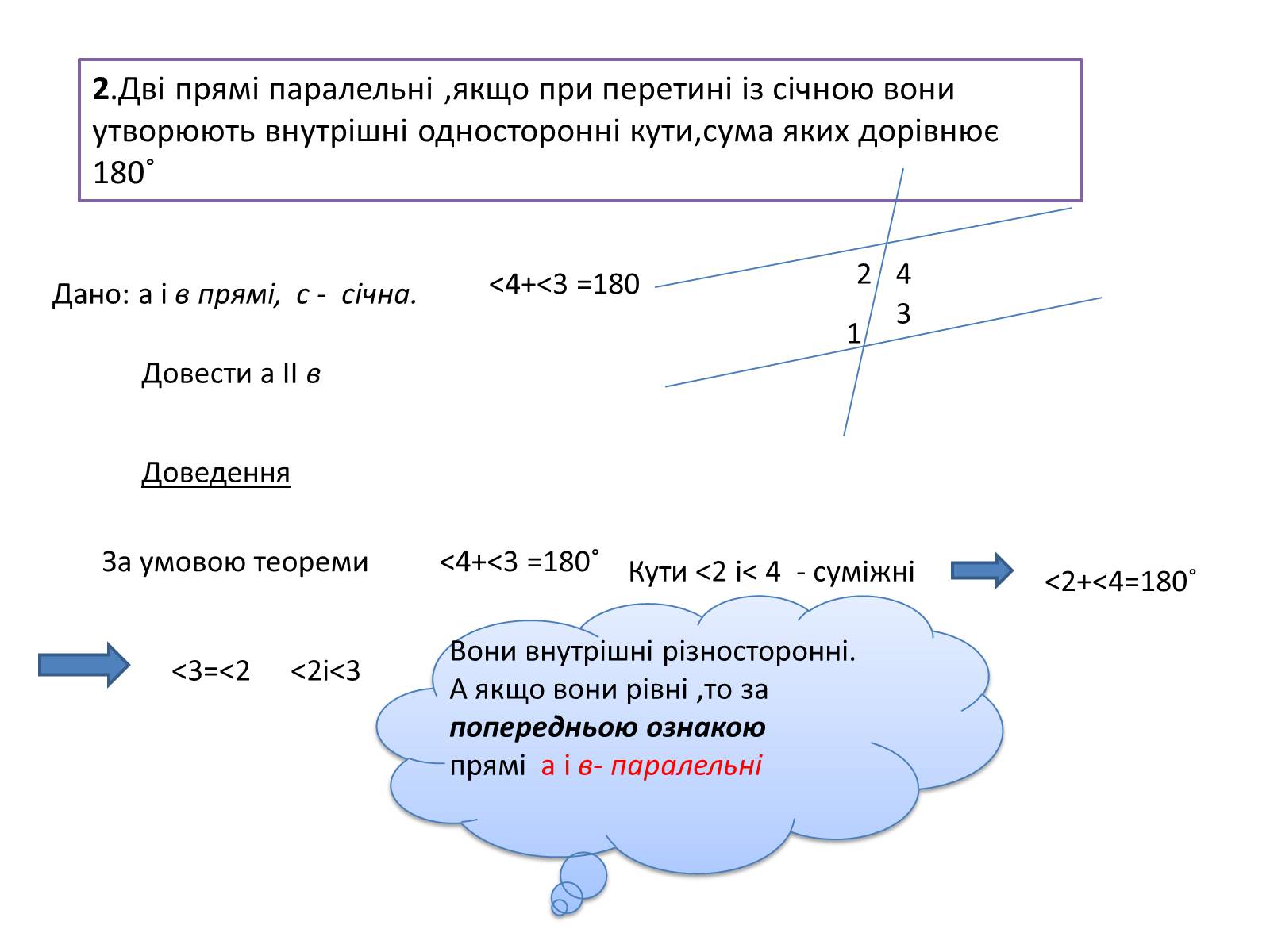
2.Дві прямі паралельні ,якщо при перетині із січною вони утворюють внутрішні односторонні кути,сума яких дорівнює 180˚
Дано: а і в прямі, с - січна.
Довести а ІІ в
1
2
3
4
<4+<3 =180
Доведення
За умовою теореми
<4+<3 =180˚
Кути <2 і< 4 - суміжні
<2+<4=180˚
<3=<2
<2i<3
Вони внутрішні різносторонні. А якщо вони рівні ,то за попередньою ознакою
прямі а і в- паралельні
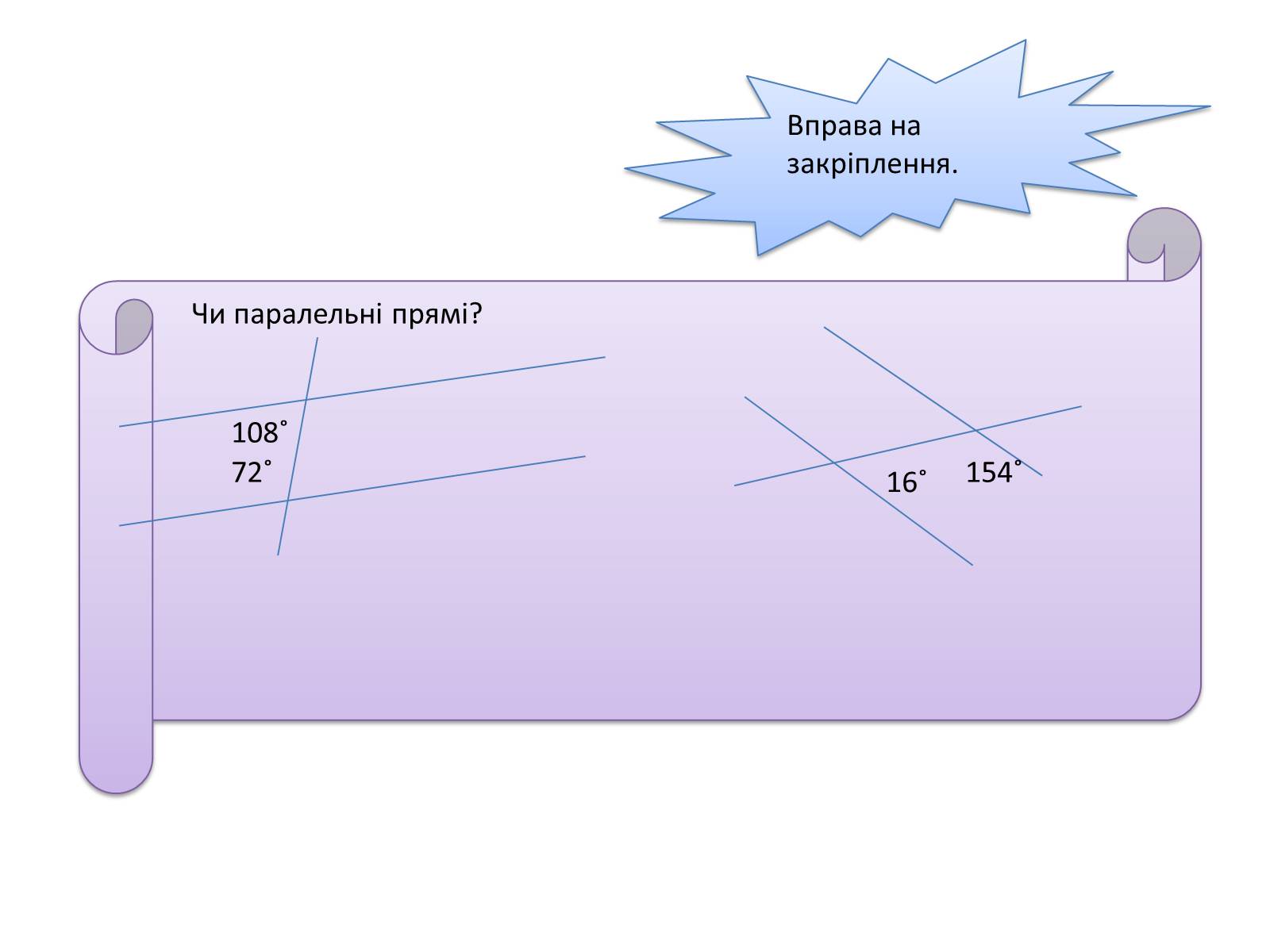
Чи паралельні прямі?
108˚
72˚
16˚
154˚
Вправа на закріплення.
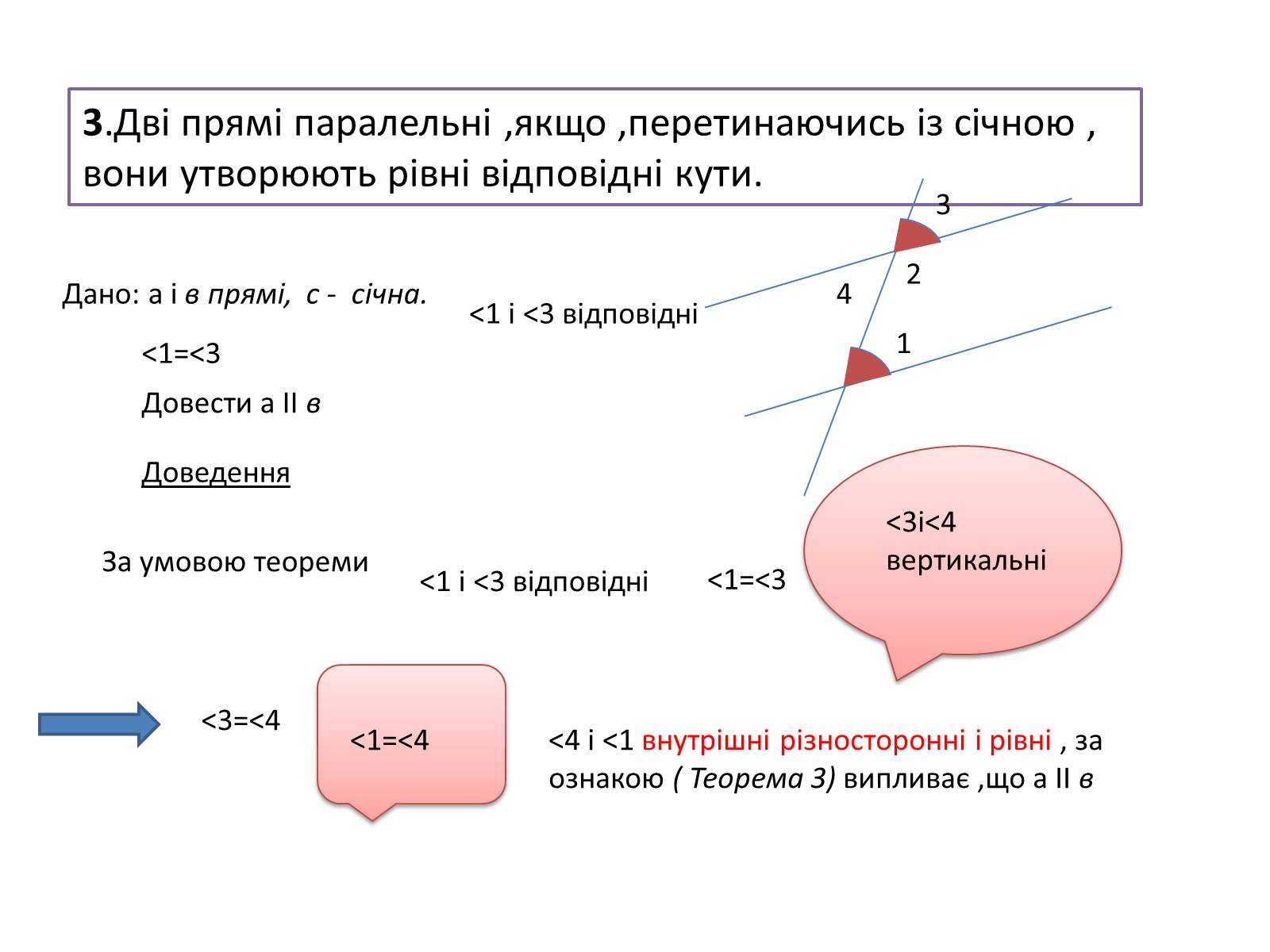
3.Дві прямі паралельні ,якщо ,перетинаючись із січною , вони утворюють рівні відповідні кути.
Дано: а і в прямі, с - січна.
1
2
3
4
<1=<3
<1 і <3 відповідні
Довести а ІІ в
Доведення
За умовою теореми
<1 і <3 відповідні
<1=<3
<3i<4 вертикальні
<3=<4
<1=<4
<4 i <1 внутрішні різносторонні і рівні , за ознакою ( Теорема 3) випливає ,що а ІІ в
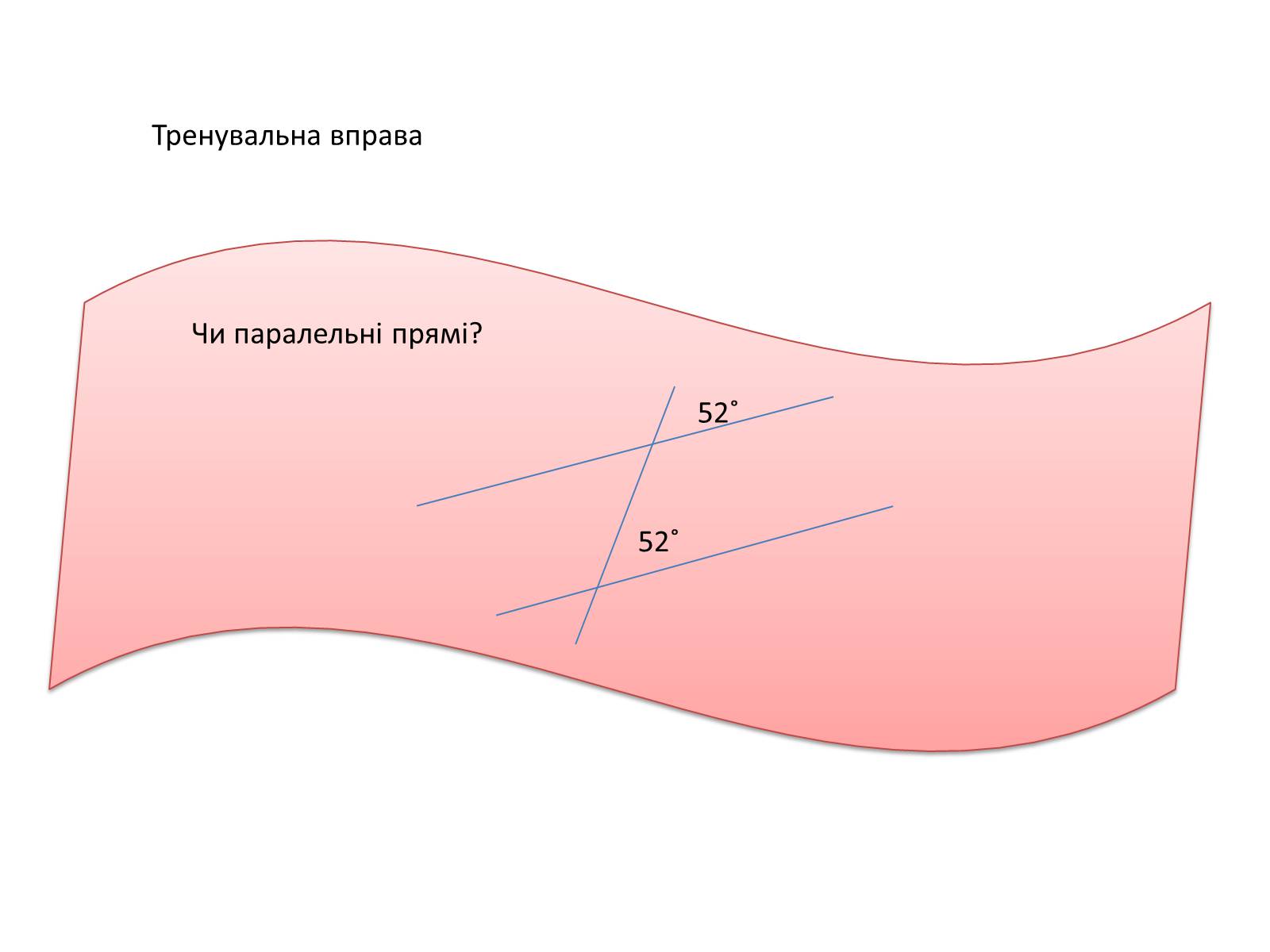
Тренувальна вправа
Чи паралельні прямі?
52˚
52˚

Дві прямі перпендикулярні до третьої прямої, паралельні
Наслідок
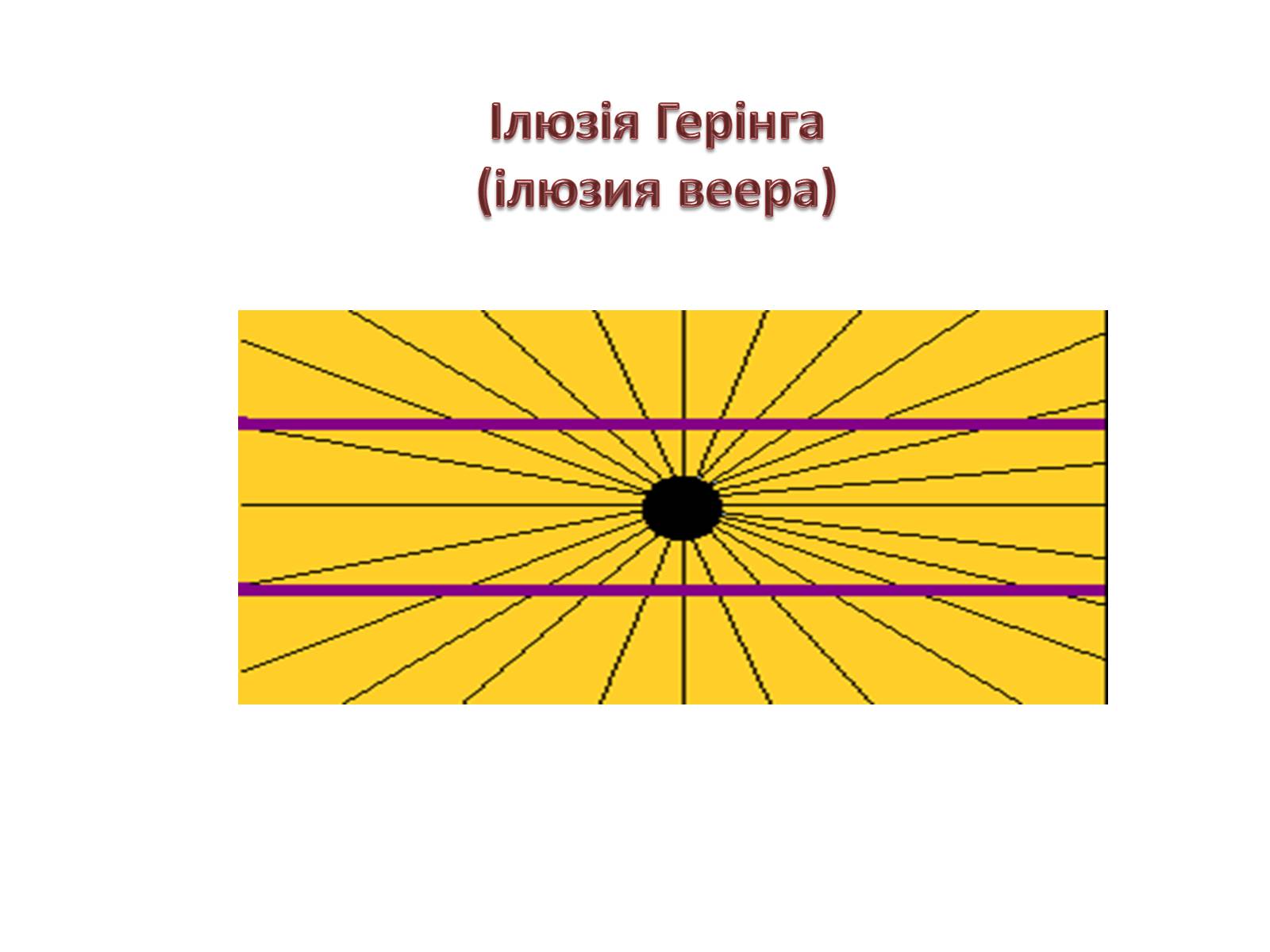
Ілюзія Герінга
(ілюзия веера)

Ілюзія кафе «Wall»
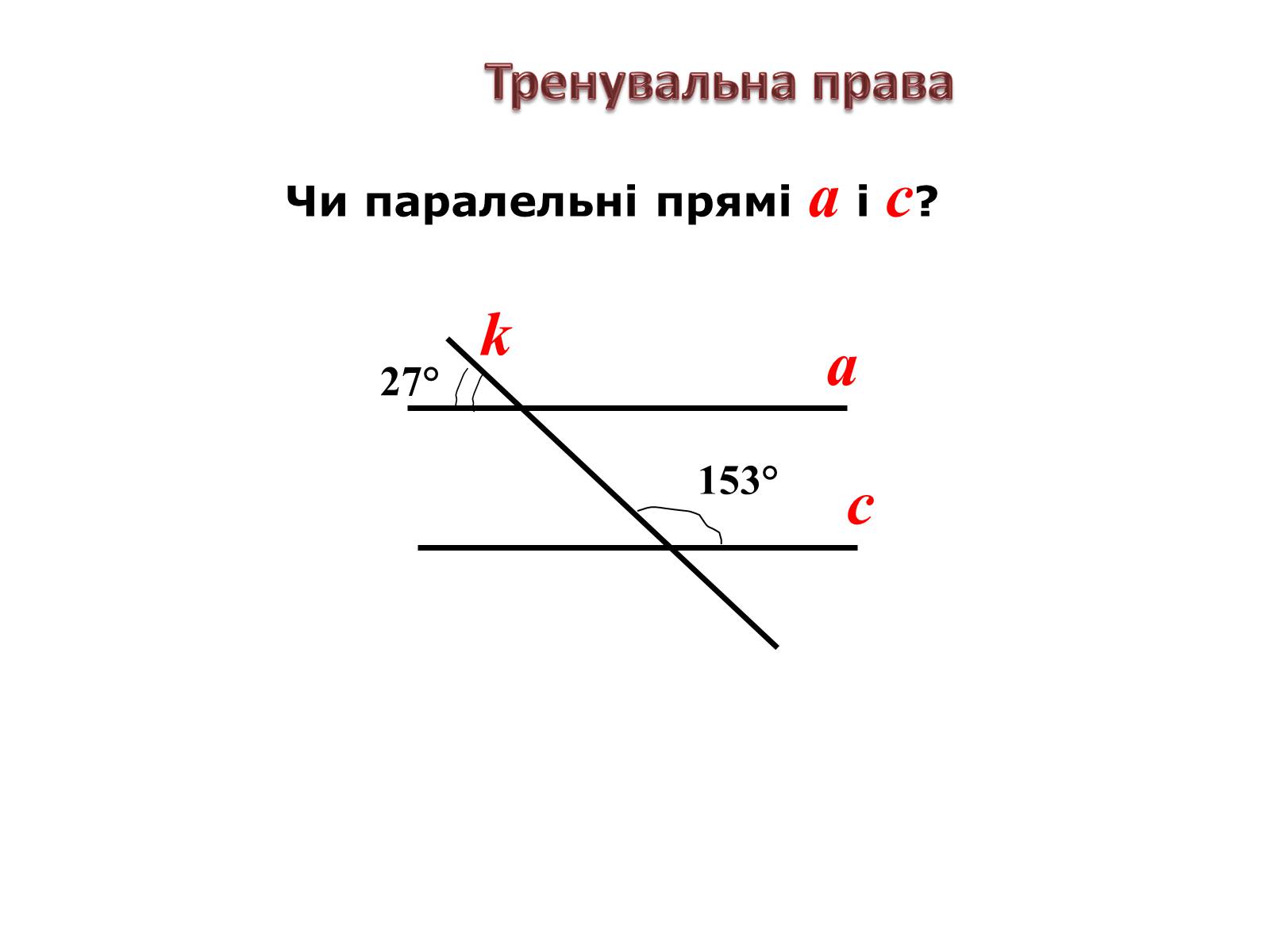
Тренувальна права
а
с
k
153°
27°
Чи паралельні прямі а і с?
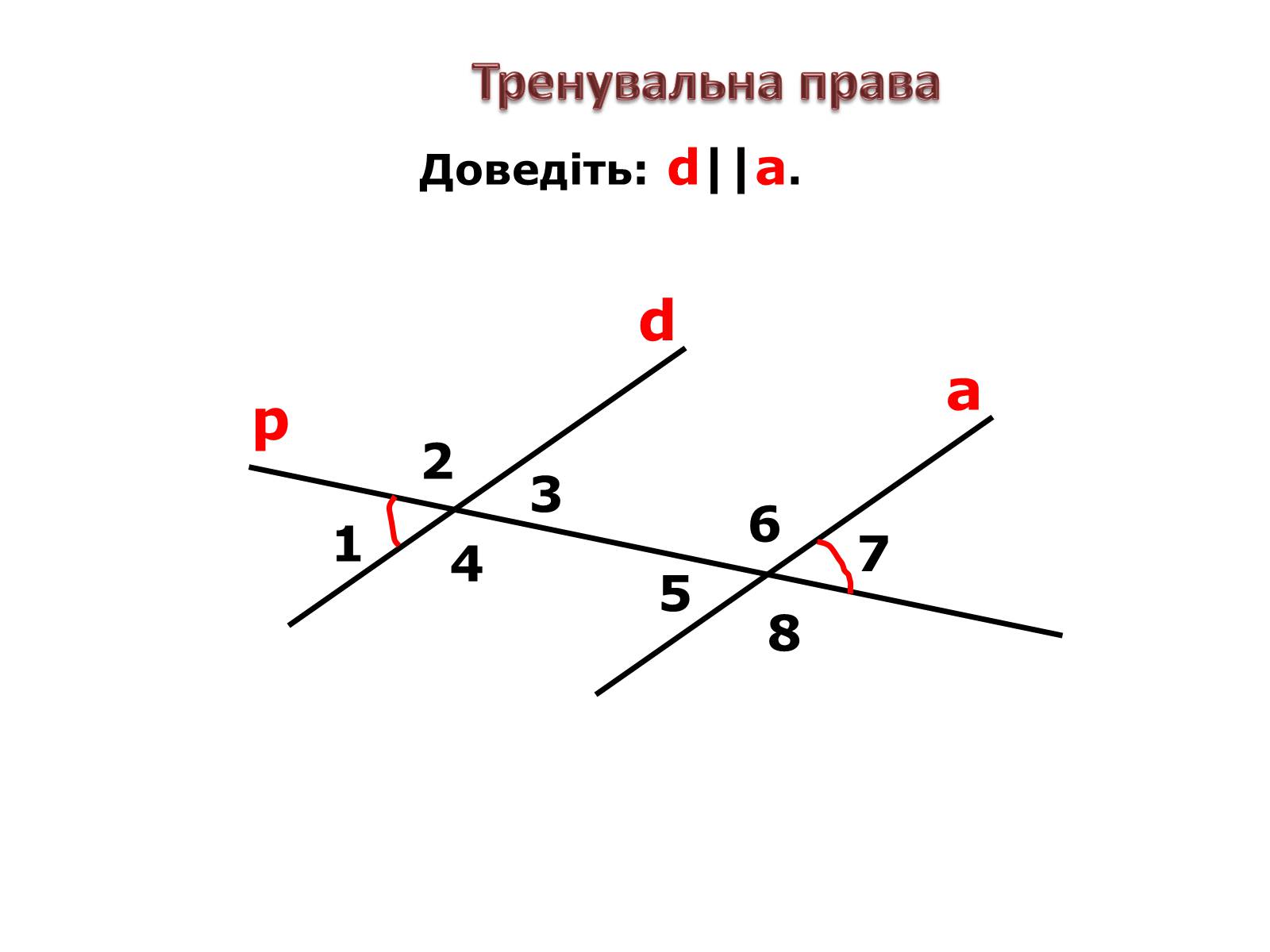
Тренувальна права
Доведіть: d||a.
d
а
1
2
3
4
5
6
7
8
р
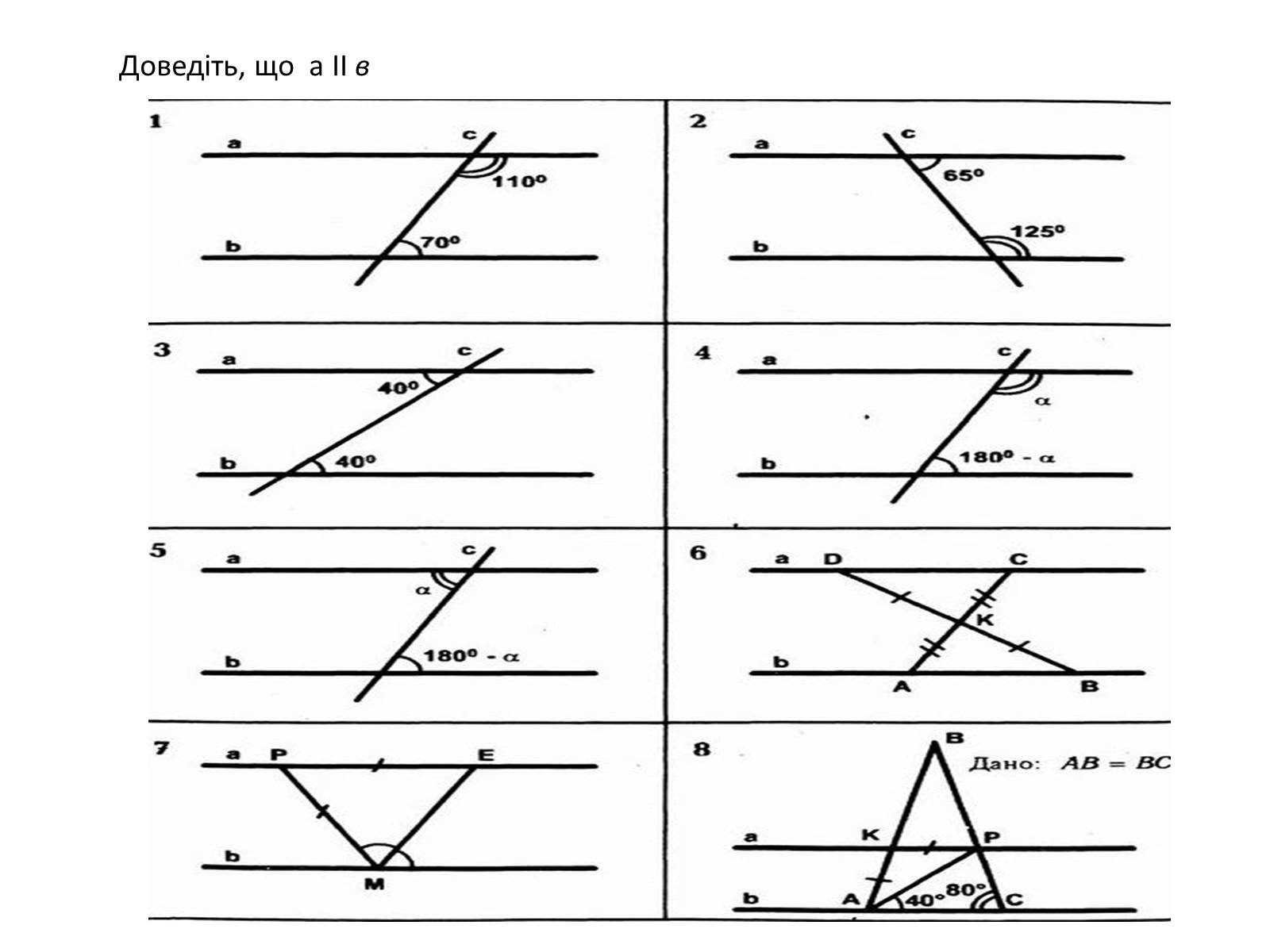
Доведіть, що а ІІ в