Презентація на тему «Означення конуса»

Означення конуса.
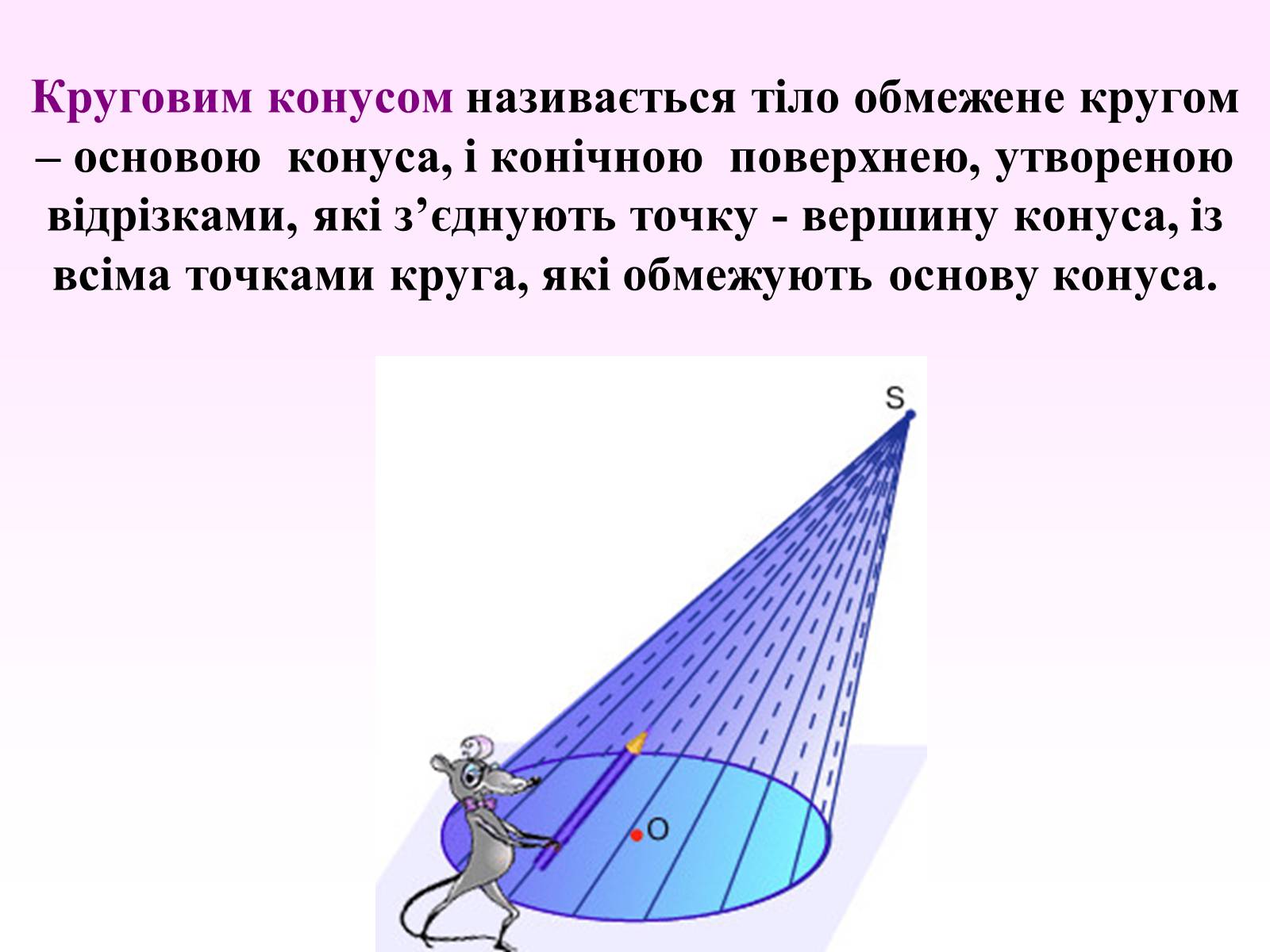
Круговим конусом називається тіло обмежене кругом – основою конуса, і конічною поверхнею, утвореною відрізками, які з'єднують точку - вершину конуса, із всіма точками круга, які обмежують основу конуса.
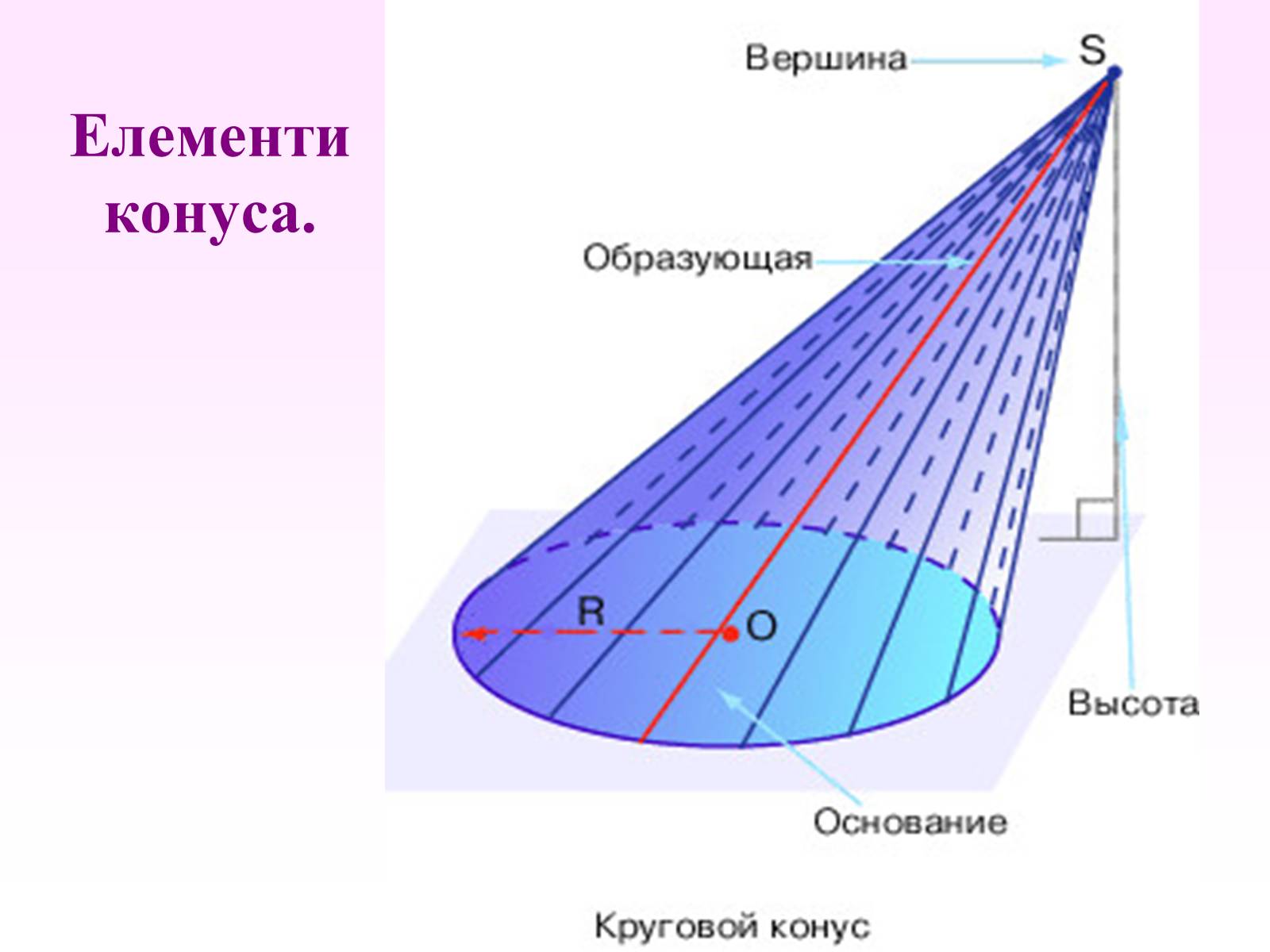
Елементи конуса.
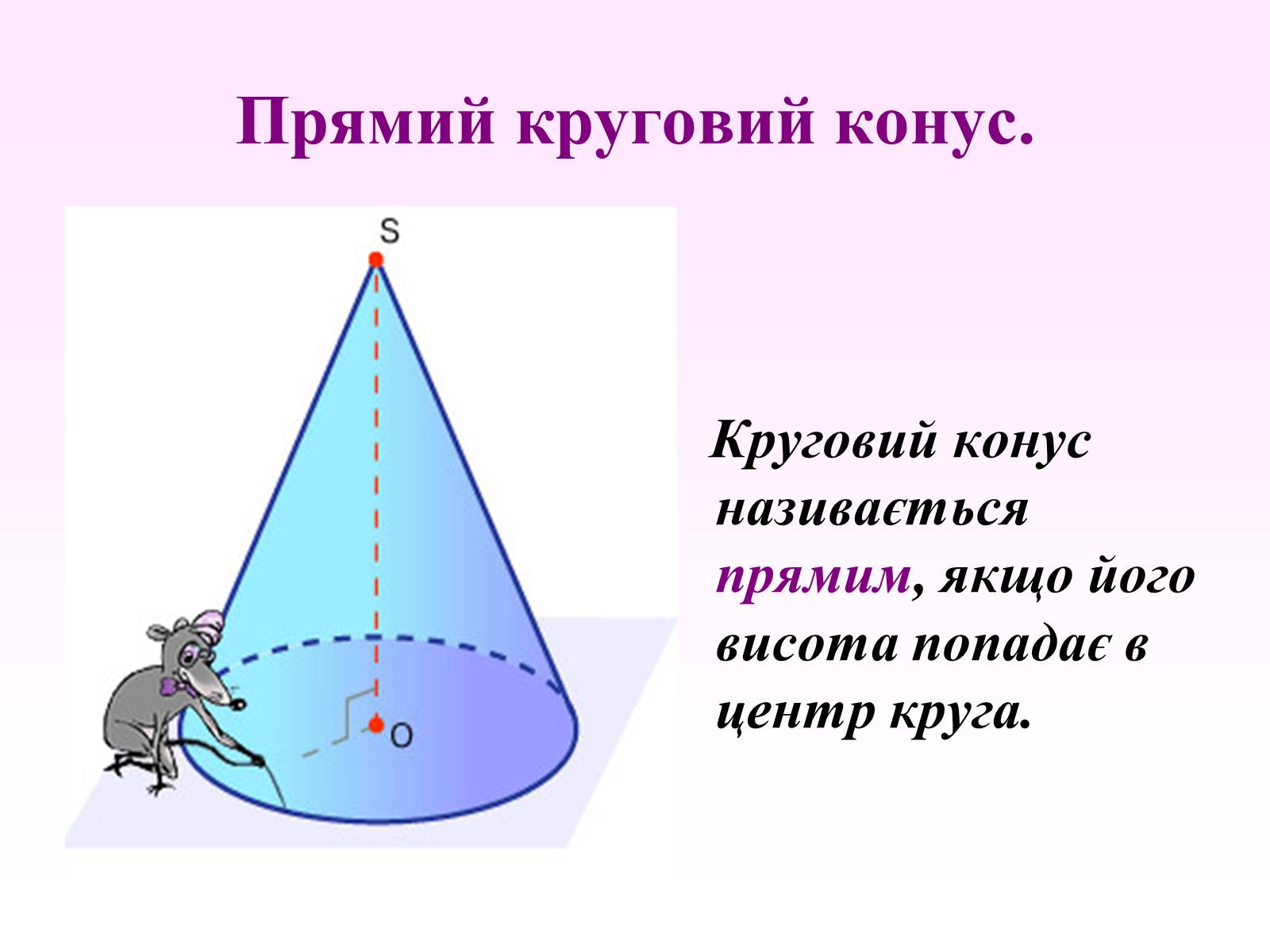
Прямий круговий конус.
Круговий конус називається прямим, якщо його висота попадає в центр круга.
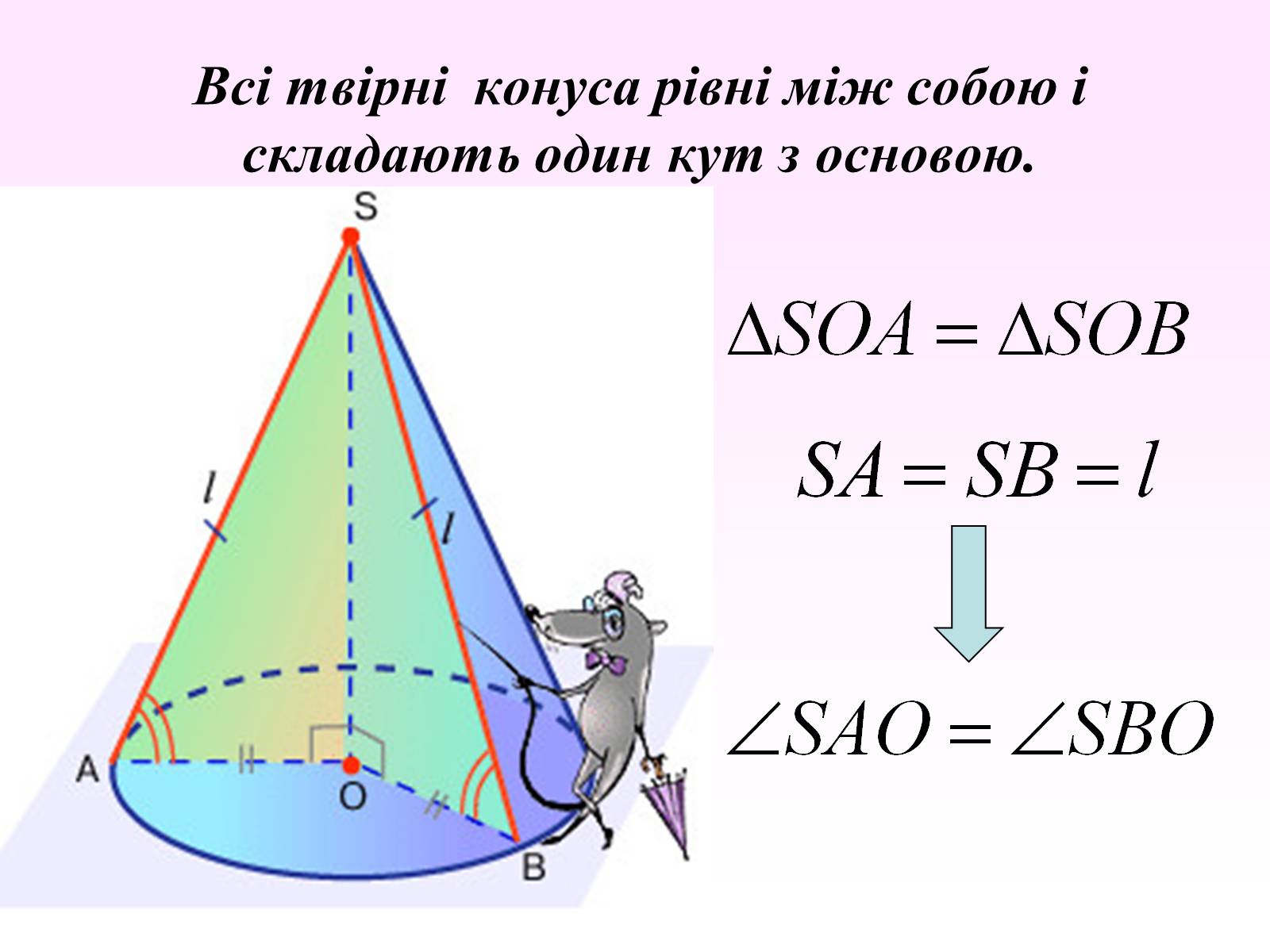
Всі твірні конуса рівні між собою і складають один кут з основою.
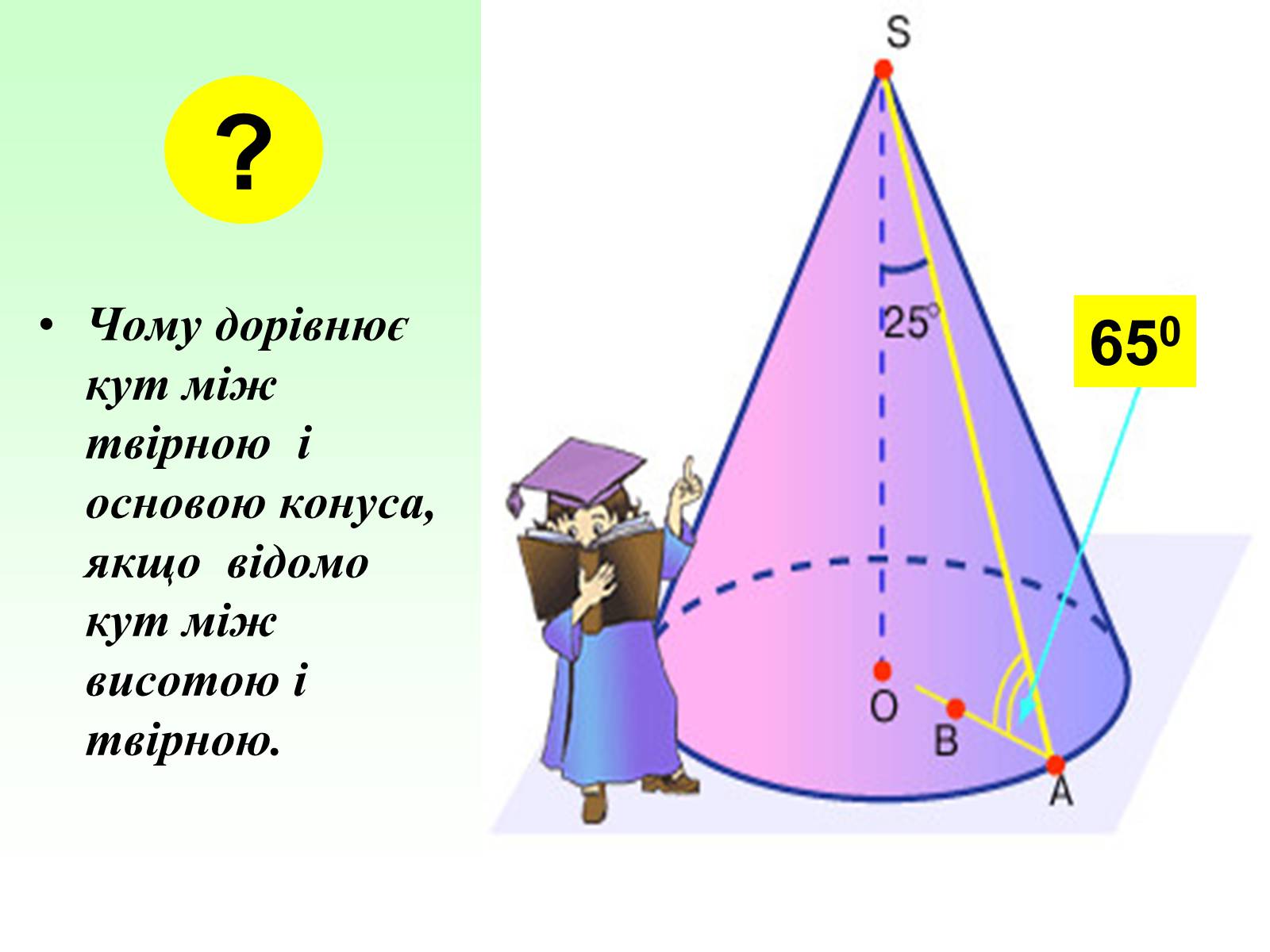
Чому дорівнює кут між твірною і основою конуса, якщо відомо кут між висотою і твірною.
?
650
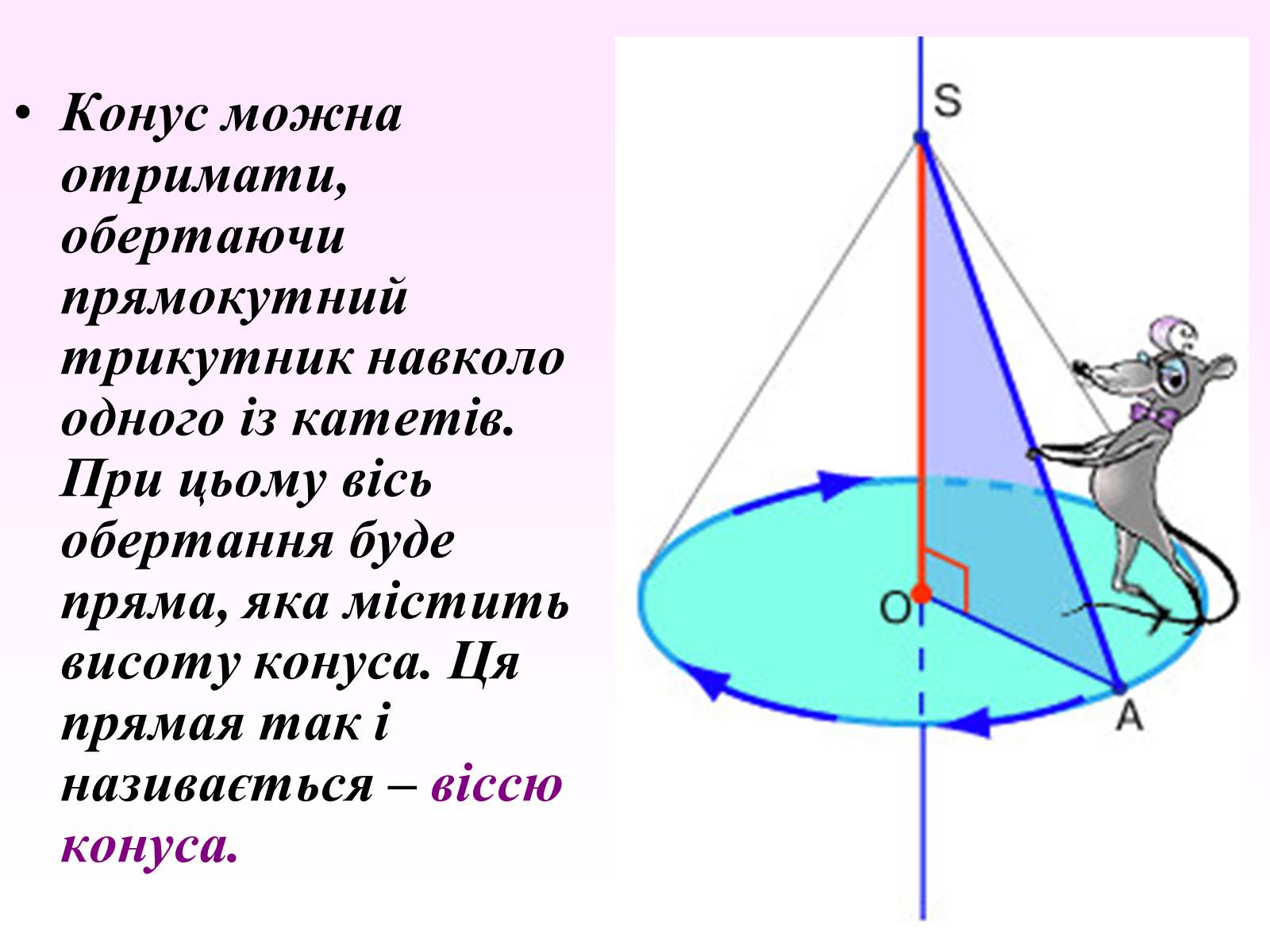
Конус можна отримати, обертаючи прямокутний трикутник навколо одного із катетів. При цьому вісь обертання буде пряма, яка містить висоту конуса. Ця прямая так і називається – віссю конуса.
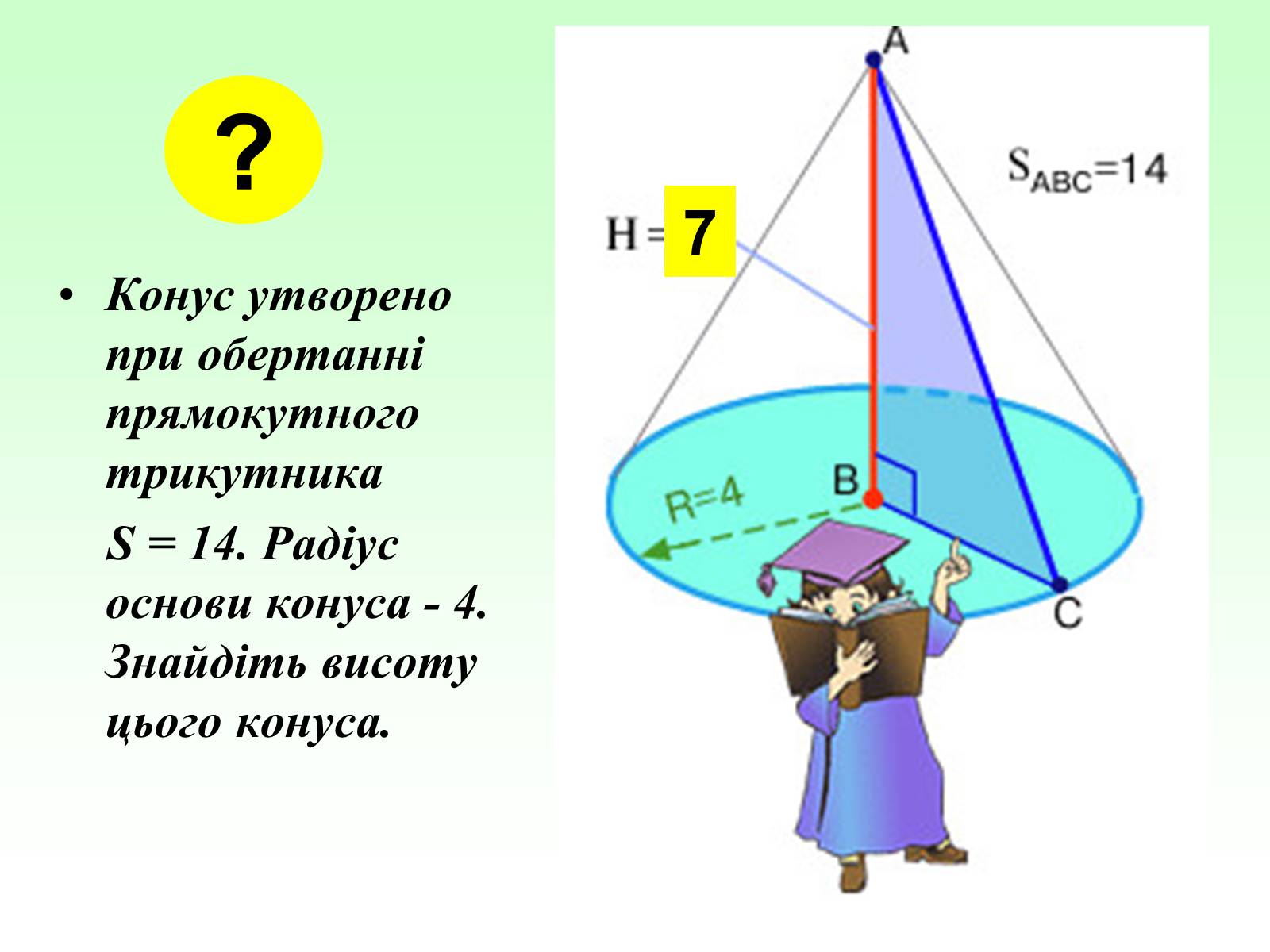
Конус утворено при обертанні прямокутного трикутника
S = 14. Радіус основи конуса - 4. Знайдіть висоту цього конуса.
?
7
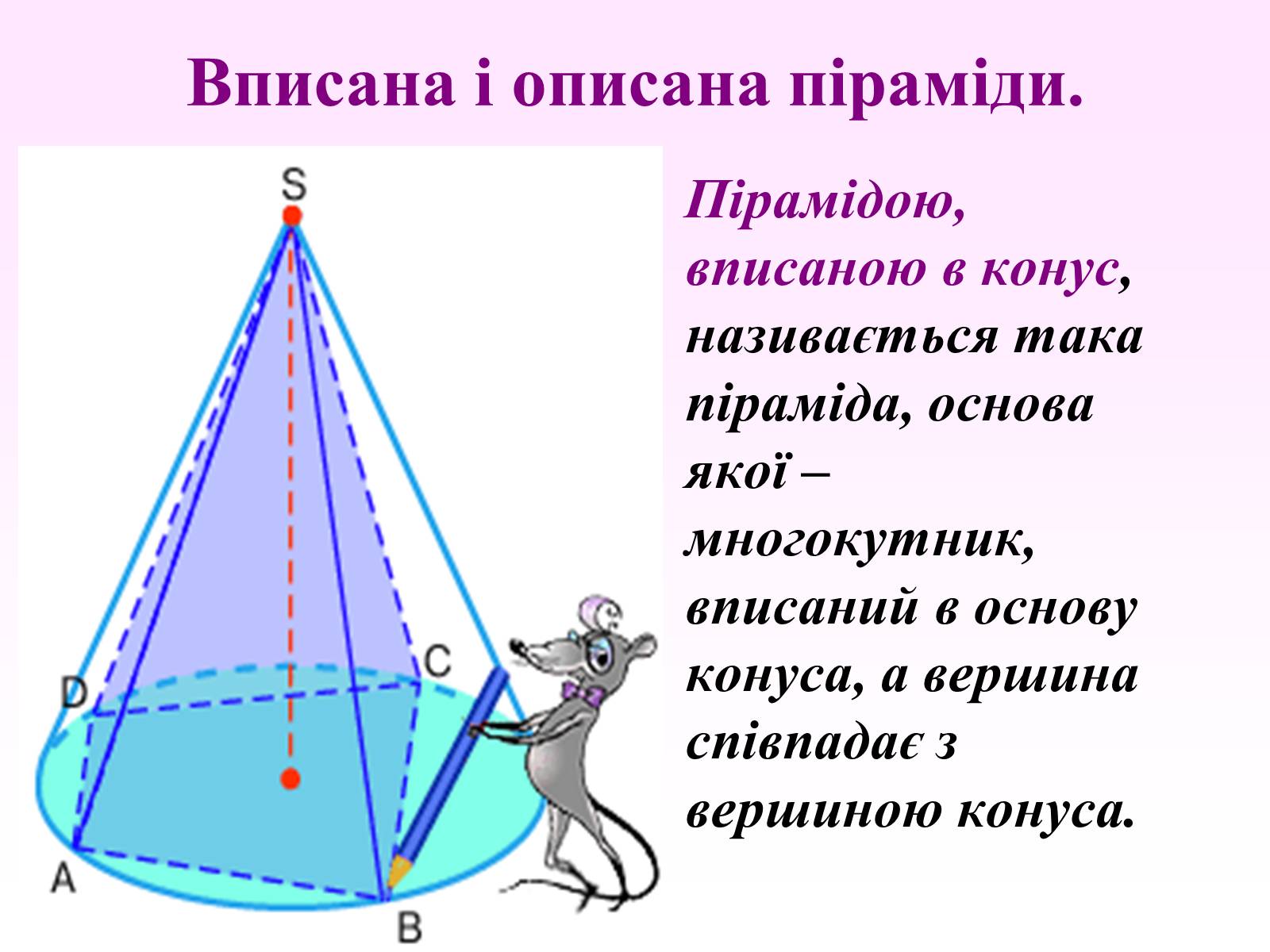
Вписана і описана піраміди.
Пірамідою, вписаною в конус, називається така піраміда, основа якої – многокутник, вписаний в основу конуса, а вершина співпадає з вершиною конуса.
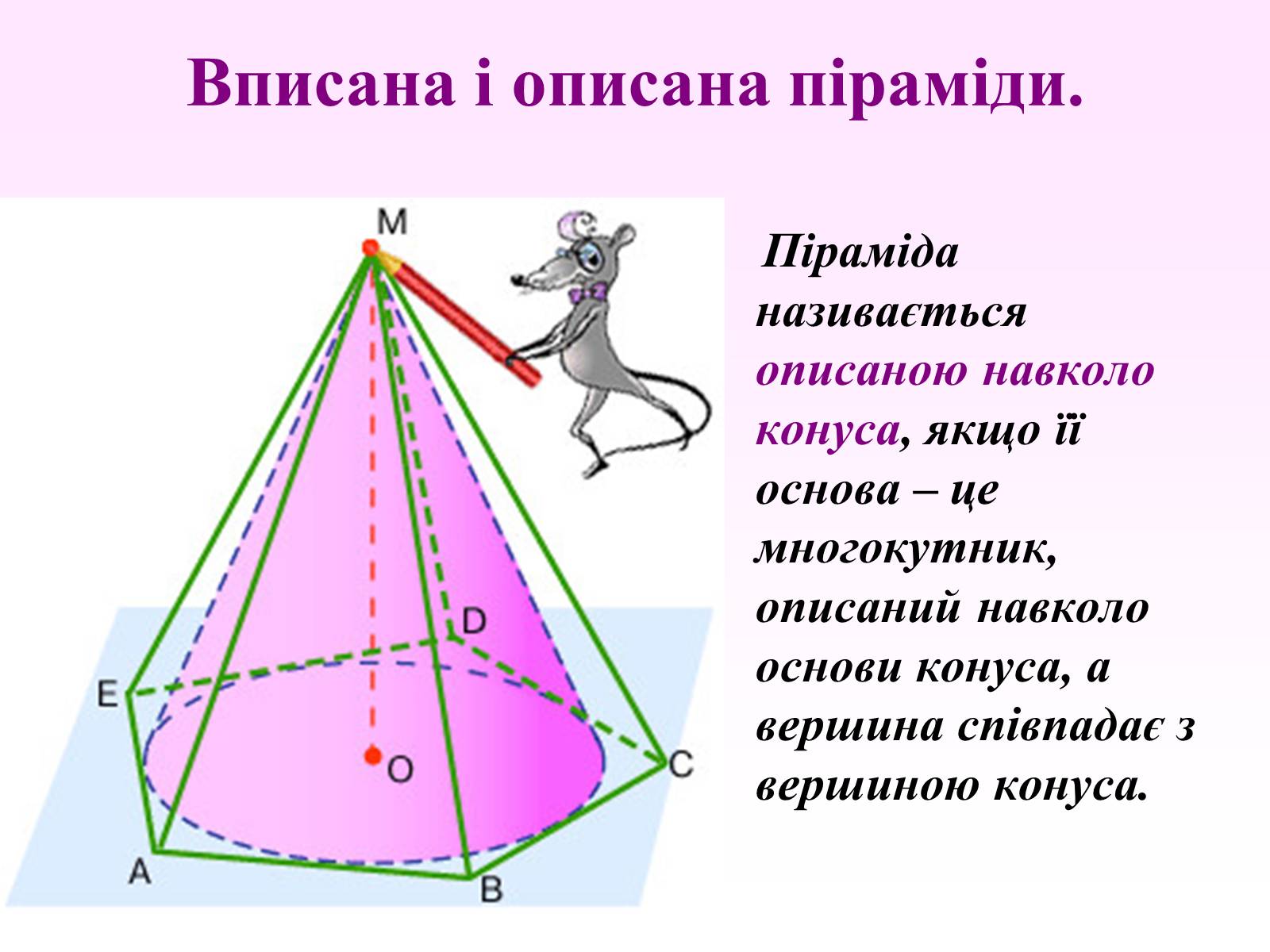
Піраміда називається описаною навколо конуса, якщо її основа – це многокутник, описаний навколо основи конуса, а вершина співпадає з вершиною конуса.
Вписана і описана піраміди.
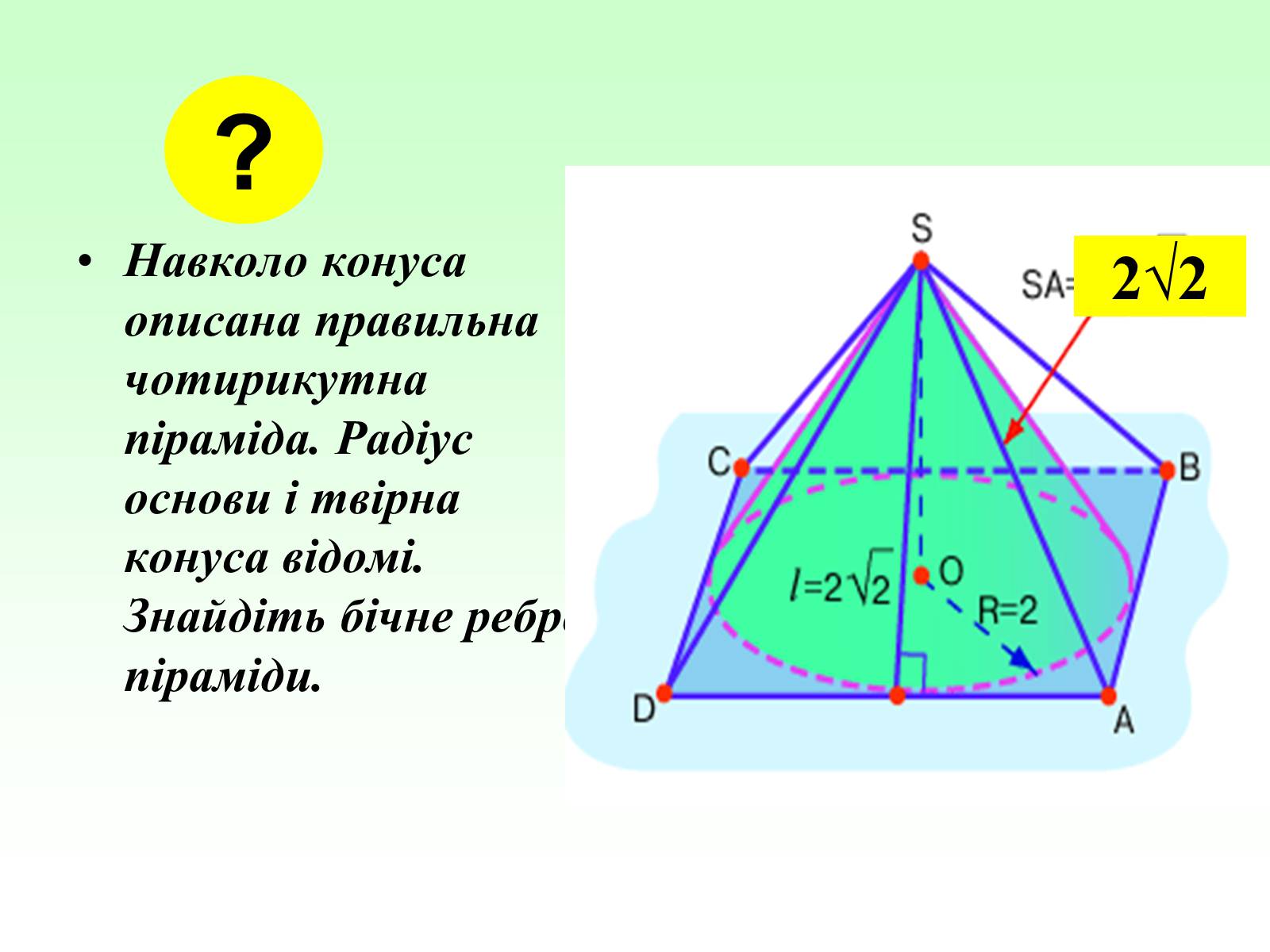
Навколо конуса описана правильна чотирикутна піраміда. Радіус основи і твірна конуса відомі. Знайдіть бічне ребро піраміди.
?
2√2
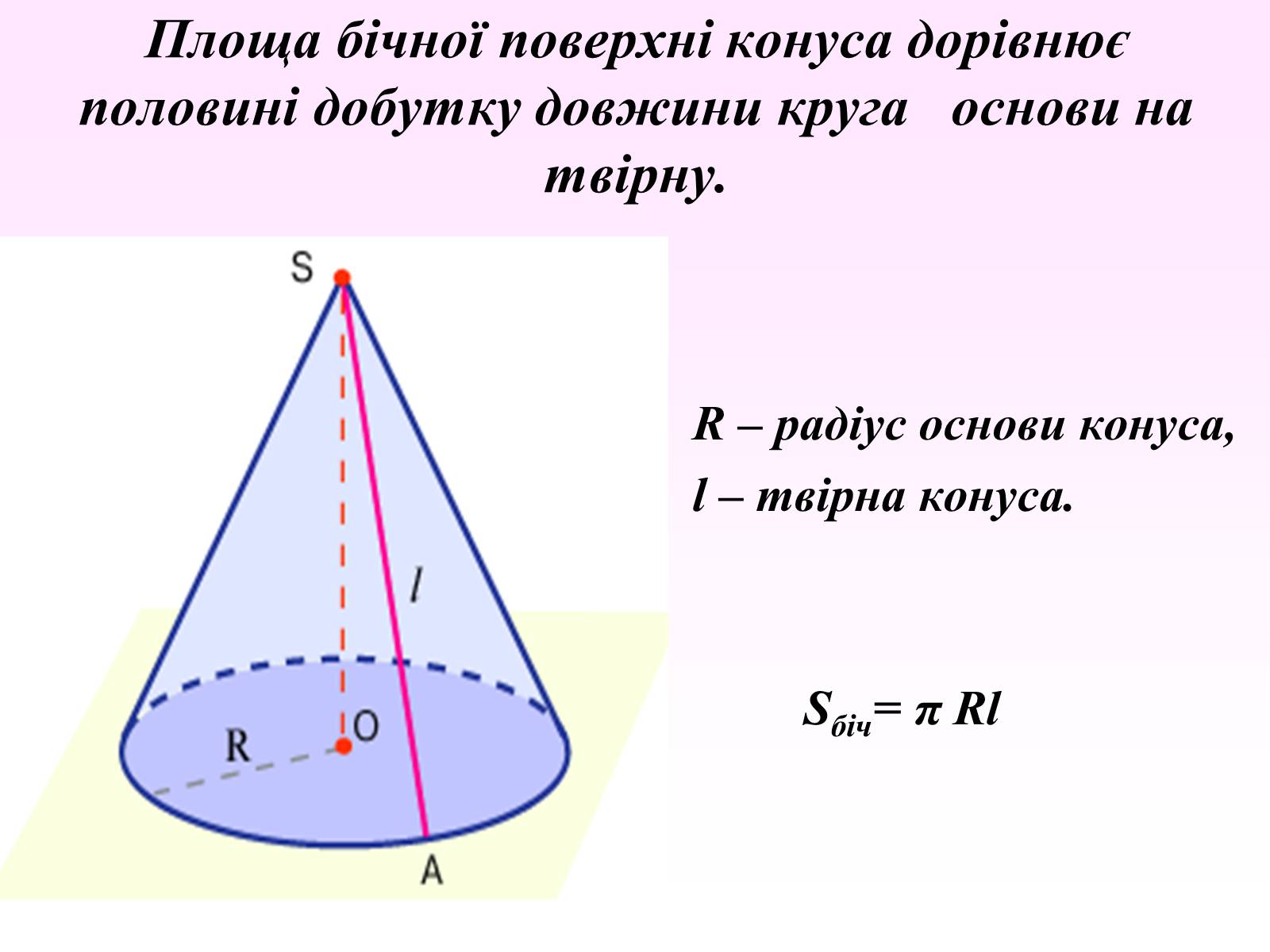
Площа бічної поверхні конуса дорівнює половині добутку довжини круга основи на твірну.
R – радіус основи конуса,
l – твірна конуса.
Sбіч= π Rl
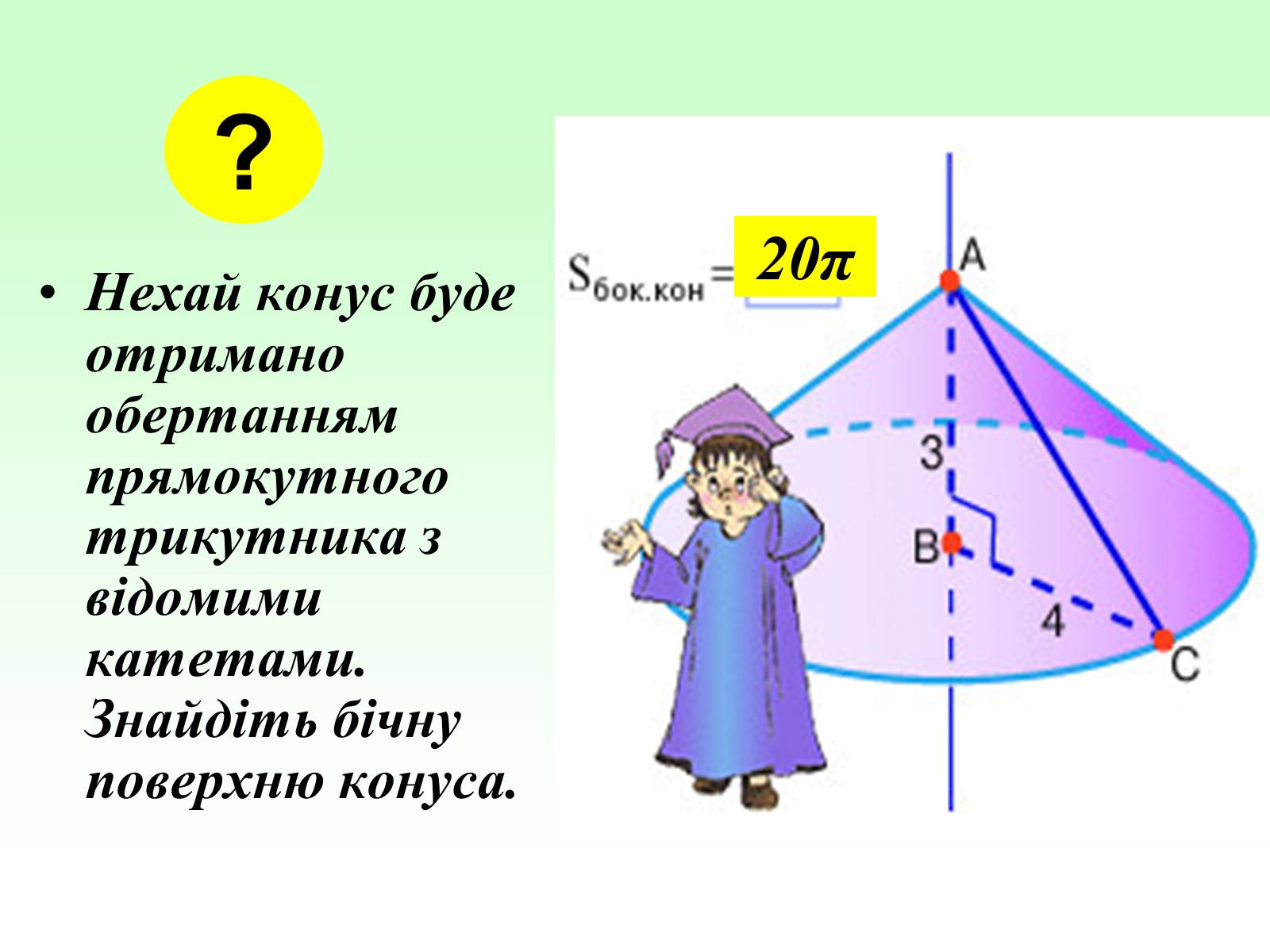
Нехай конус буде отримано обертанням прямокутного трикутника з відомими катетами. Знайдіть бічну поверхню конуса.
?
20π
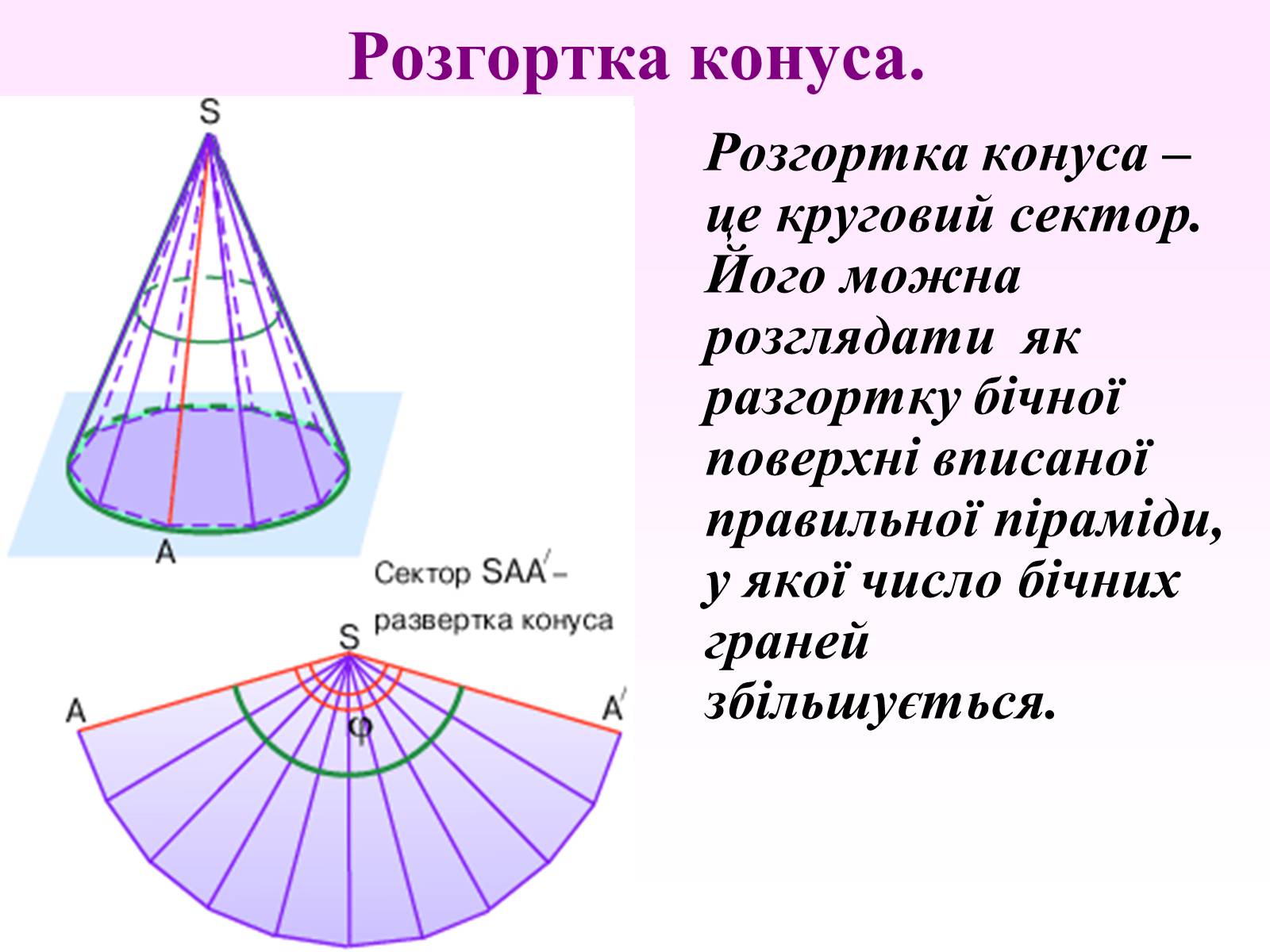
Розгортка конуса.
Розгортка конуса – це круговий сектор. Його можна розглядати як разгортку бічної поверхні вписаної правильної піраміди, у якої число бічних граней збільшується.
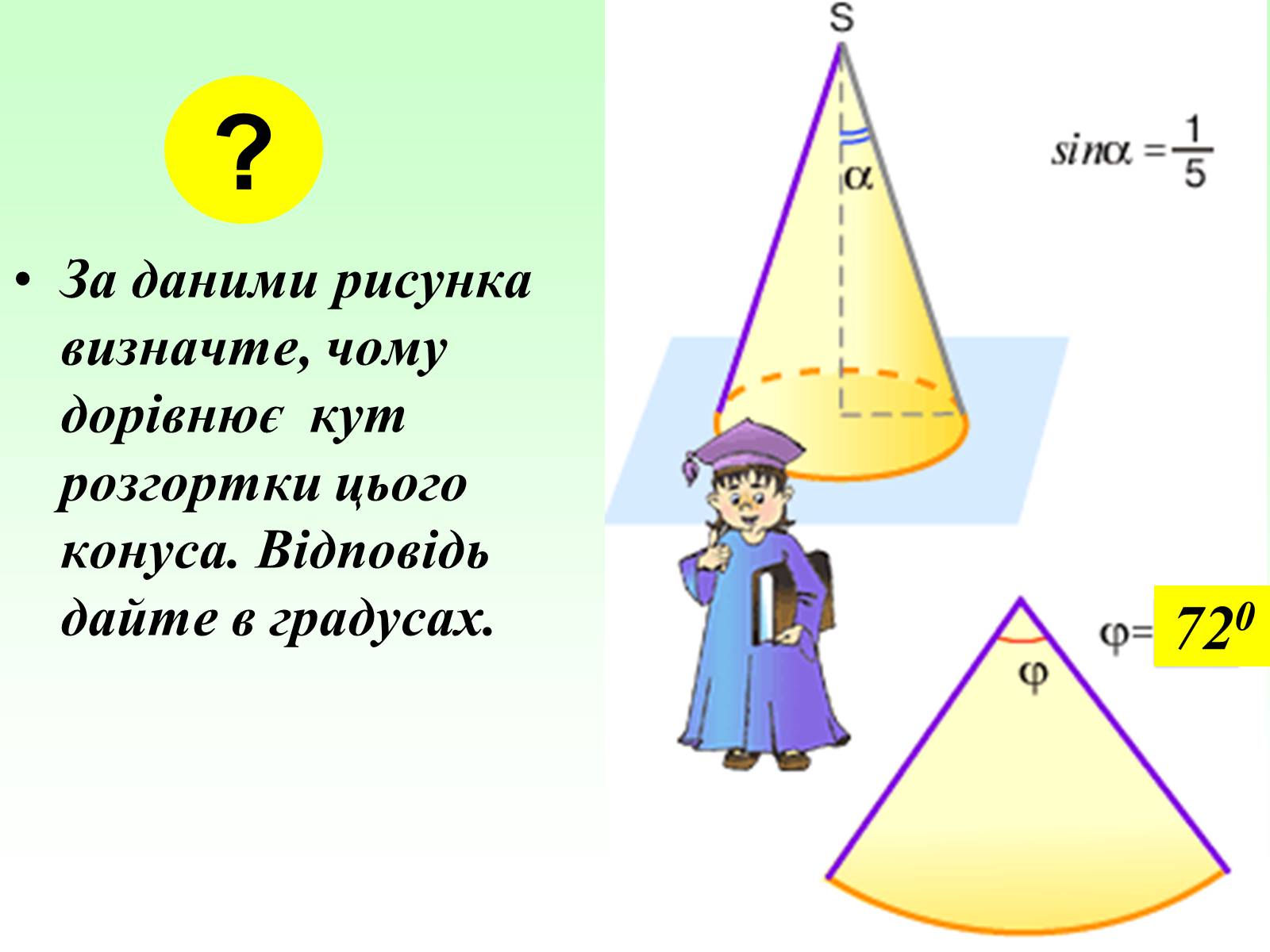
За даними рисунка визначте, чому дорівнює кут розгортки цього конуса. Відповідь дайте в градусах.
?
720
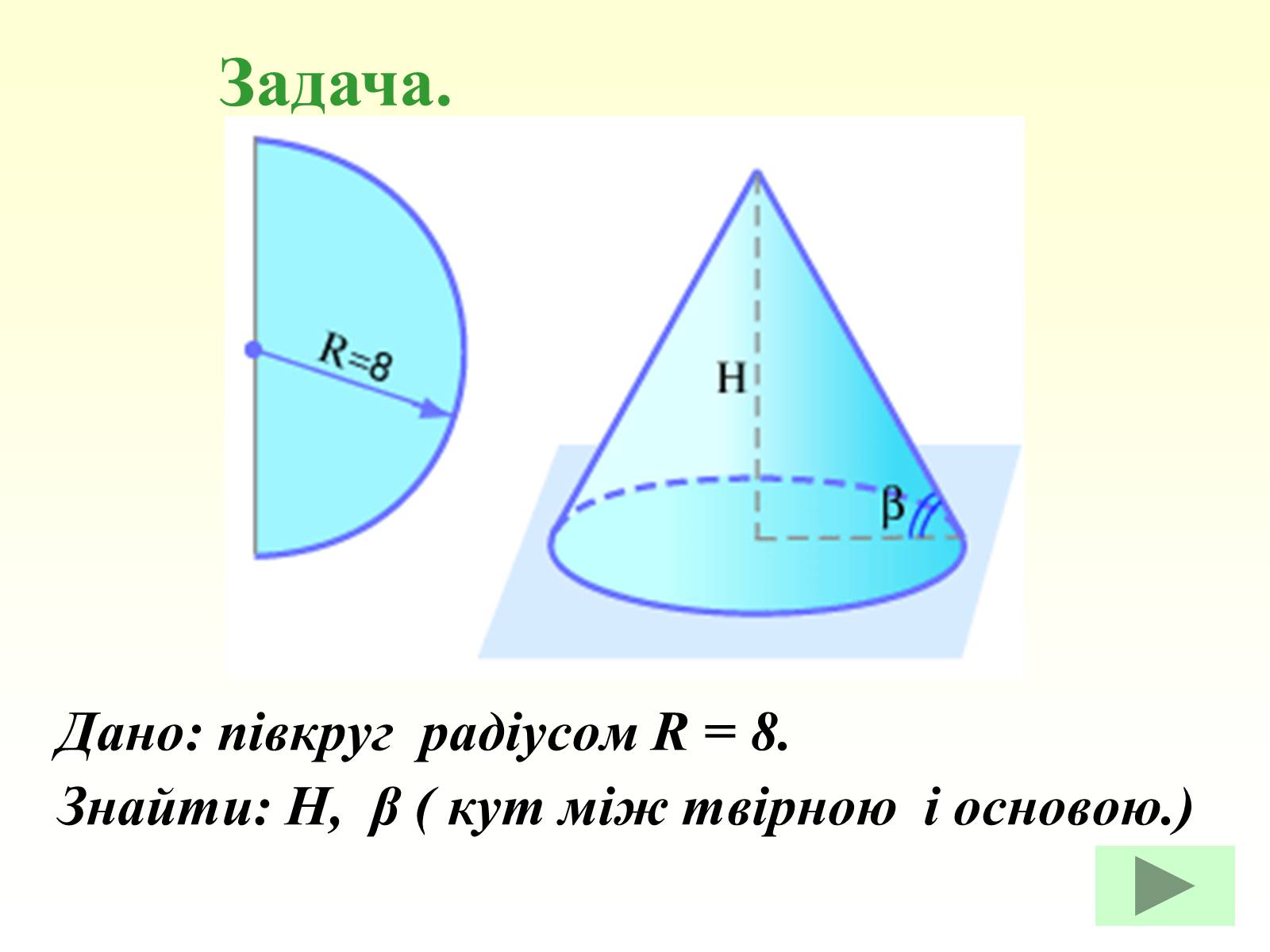
Дано: півкруг радіусом R = 8.
Знайти: Н, β ( кут між твірною і основою.)
Задача.
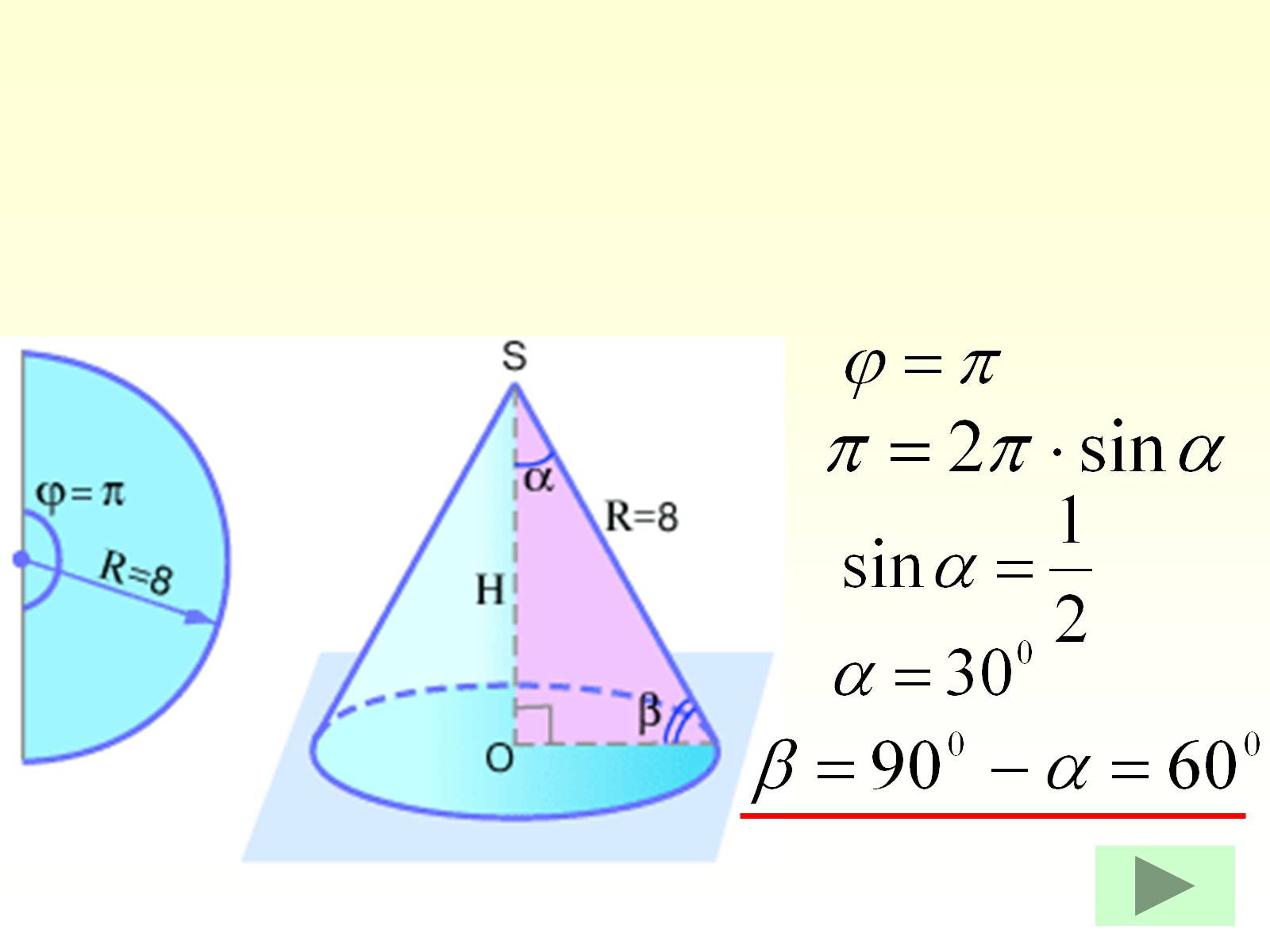
Дано: півкруг радіусом R = 8.
Знайти: Н, β ( кут між твірною і основою.)
Задача.
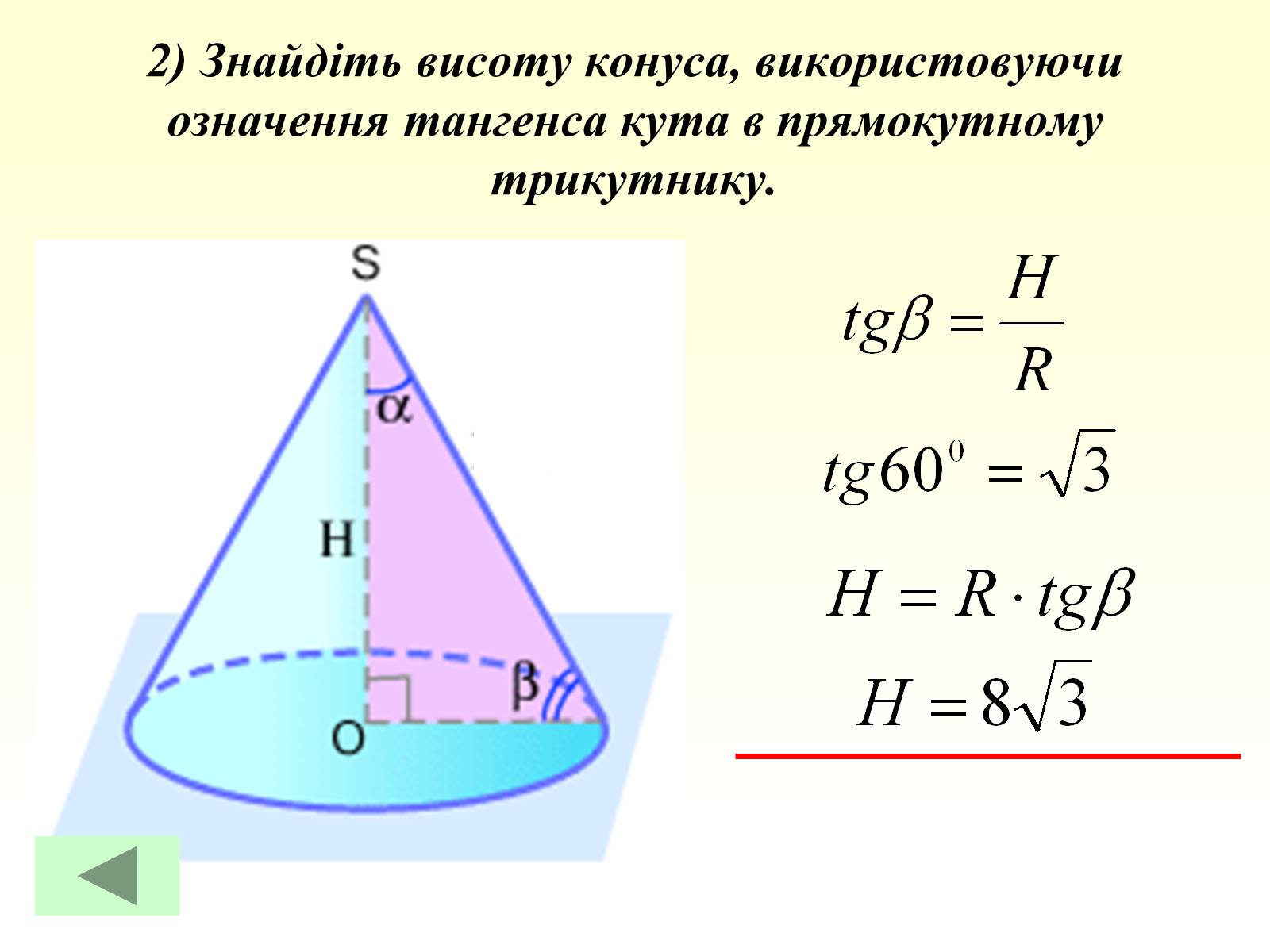
2) Знайдіть висоту конуса, використовуючи означення тангенса кута в прямокутному трикутнику.