Презентація на тему «Математика в архитектуре»

Математика в архитектуре

Тесная связь архитектуры и математики известна давно. В Древней Греции – геометрия считалась одним из разделов архитектуры. Современный архитектор должен быть знаком с различными соотношениями ритмических рядов, позволяющих сделать объект наиболее гармоничным и выразительным. Кроме того, он должен знать аналитическую геометрию и математический анализ, основы высшей алгебры и теории матриц, владеть методами математического моделирования и оптимизации. Не случайно при подготовке архитекторов за рубежом большое внимание уделяется математической подготовке и владению компьютером.

Золотое сечение
Использование золотой пропорции в архитектуре:
Знаменитый русский архитектор М.Ф.Казаков широко использовал в своем творчестве золотое сечение. Его талант был многогранным, но в большей степени он проявился в многочисленных проектах жилых домов и усадеб. Архитектурный шедевр Москвы - дом Пашкова - является одним из наиболее совершенных произведений архитектора В.Баженова. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 году.

Храм Василия Блаженного

Золотое сечение в пропорциях Парфенона

Золотое сечение в пропорциях Парфенона
Золотое сечение в пропорциях Парфенона

Так же в архитектуре широко использовались различные виды симметрии. «Симметрия» по-гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей». Современные архитекторы всех стран продолжают использовать в своей работе опыт старых мастеров: проверенные временем золотую пропорцию и симметрию.

Симметрия воспринимается человеком как проявление закономерности, а значит внутреннего порядка. Внешне этот внутренний порядок воспринимается как красота.Симметричные объекты обладают высокой степенью целесообразности – ведь симметричные предметы обладают большей устойчивостью и равной функциональностью в разных направлениях. Все это привело человека к мысли, что чтобы сооружение было красивым оно должно быть симметричным.

Симметрия воспринимается человеком как проявление закономерности, а значит внутреннего порядка. Внешне этот внутренний порядок воспринимается как красота.Симметричные объекты обладают высокой степенью целесообразности – ведь симметричные предметы обладают большей устойчивостью и равной функциональностью в разных направлениях. Все это привело человека к мысли, что чтобы сооружение было красивым оно должно быть симметричным.

Как математика помогает добиться прочности сооружений.
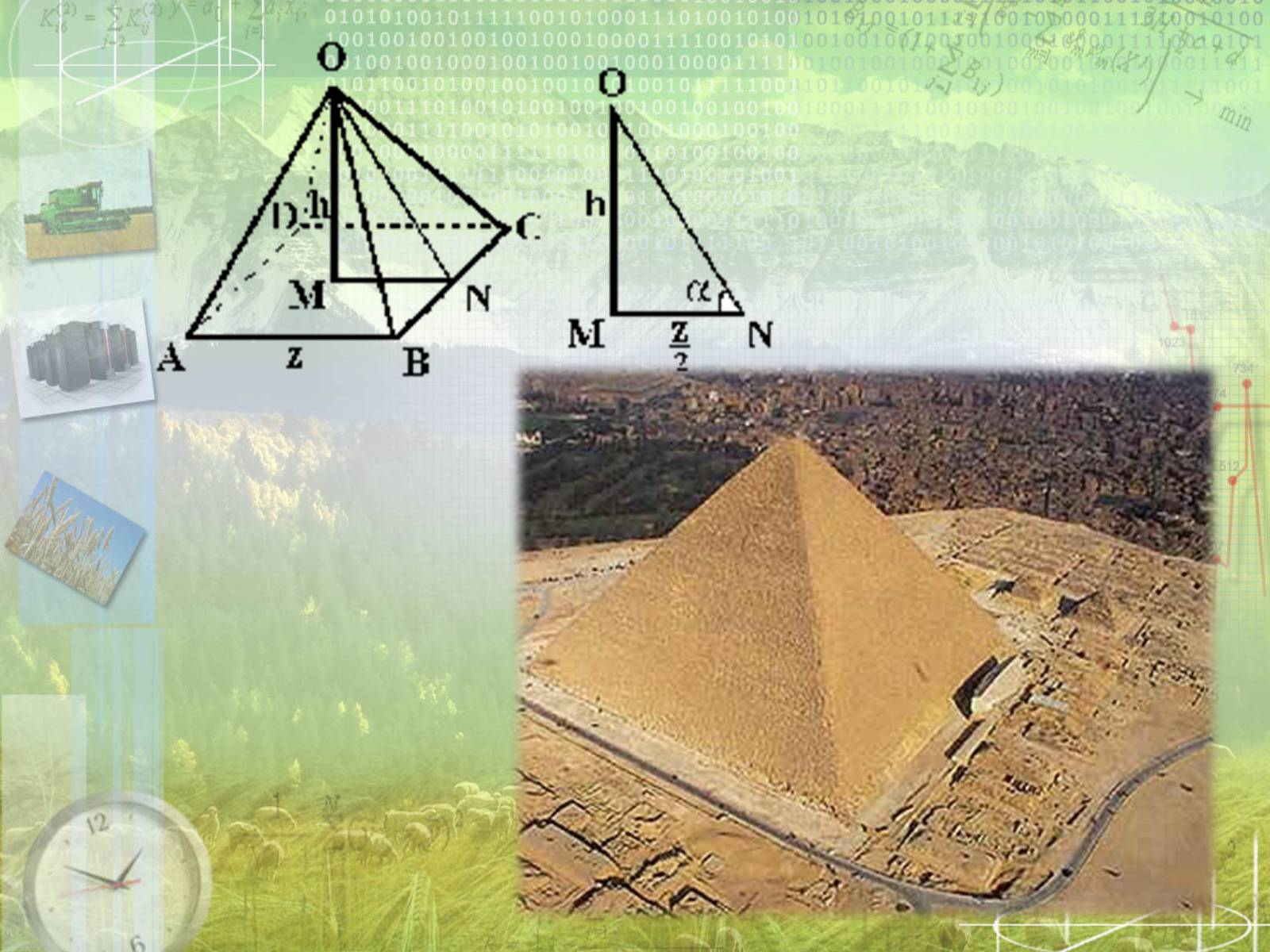
Люди с древних времен, возводя свои жилища, думали, в первую очередь, об их прочности. Прочность сооружения обеспечивается не только материалом, из которого оно создано, но и конструкцией, которая используется в качестве основы при его проектировании и строительстве. Прочность сооружения напрямую связана с той геометрической формой, которая является для него базовой. Математик бы сказал, что здесь очень важна геометрическая форма (тело), в которое вписывается сооружение.Самым прочным архитектурным сооружением с давних времен считаются египетские пирамиды. Как известно они имеют форму правильных четырехугольных пирамид.Именно эта геометрическая форма обеспечивает наибольшую устойчивость за счет большой площади основания.

Этапом развития архитектурных конструкций явилась каркасная система. Аркбутаны являлись каркасом, которые окружал сооружение и принимал на себя основные нагрузки. Арочная конструкция послужила прототипом каркасной конструкции, которая сегодня используется в качестве основной при возведении современных сооружений из металла, стекла и бетона. Достаточно вспомнить конструкции известных башен: Эйфелевой башни в Париже и телебашни на Шаболовке.

Другой интересной для архитекторов геометрической поверхностью оказался гиперболический параболоид. Это поверхность, которая в сечении имеет параболы и гиперболу. Появление новых строительных материалов делает возможным создание тонкого железобетонного каркаса и стен из стекла. Достаточно вспомнить американские небоскребы или, например, здание Кремлевского дворца съездов созданных из стекла и бетона. Именно эти материалы и каркасные конструкции стали преобладающими в архитектурных сооружениях XX века. Они обеспечивают зданиям высокую степень прочности.

Ни один из видов искусств так тесно не связан с геометрией как архитектура.
Архитектурные произведения живут в пространстве, являются его частью, вписываясь в определенные геометрические формы. Кроме того, они состоят из отдельных деталей, каждая из которых также строится на базе определенного геометрического тела. Часто геометрические формы являются комбинациями различных геометрических тел.

Геометрическая форма сооружения настолько важна, что бывают случаи, когда в имени или названии здания закрепляются названия геометрических фигур. Так, здание военного ведомства США носит название Пентагон, что означает пятиугольник. Связано это с тем, что, если посмотреть на это здание с большой высоты, то оно действительно будет иметь вид пятиугольника. На самом деле только контуры этого здания представляют пятиугольник. Само же оно имеет форму многогранника.

В Спасской башне Московского кремля в основании можно увидеть прямой параллелепипед, переходящий в средней части в фигуру, приближающуюся к цилиндру, завершается же она пирамидой. При более детальном рассмотрении и изучении деталей можно увидеть: круги – циферблаты курантов; шар – основание для крепления рубиновой звезды; полукруги – арки одного из рядов бойниц на фасаде башни и т.д. Таким образом, можно говорить о пространственных геометрических фигурах, которые служат основой сооружения в целом или отдельных его частей, а также плоских фигурах, которые обнаруживаются на фасадах зданий.

Антисимметрия это противоположность симметрии, ее отсутствие. Примером антисимметрии в архитектуре является Собор Василия Блаженного в Москве, где симметрия отсутствует полностью в сооружении в целом.
Однако, удивительно,
что отдельные части
этого собора
симметричны и
это создает
его гармонию.

Диссимметрия – это частичное отсутствие симметрии, расстройство симметрии, выраженное в наличии одних симметричных свойств и отсутствии других. Примером диссимметрии в архитектурном сооружении может служить Екатерининский дворец в Царском селе под Санкт-Петербургом. Практически в нем полностью выдержаны все свойства симметрии за исключением одной детали.
Наличие Дворцовой церкви расстраивает симметрию здания в целом. Если же
не принимать во
внимание эту
церковь, то Дворец
становится
симметричным.

Вывод:
Математика предлагает архитектору ряд, если так можно назвать, общих правил организации частей в целое, которые помогают:
Расположить эти части в пространстве, так, что в них проявлялся порядок;
Установить определенное соотношение между размерами частей и задать для изменения размеров (уменьшения или увеличения) определенную единую закономерность, что обеспечивает восприятие целостности и представление о порядке;
Выделить определенное место в пространстве, где будет размещаться сооружение, описать его определенной математической формой, которая также позволит выделить его из других сооружений и внести в их состав, создав новую композицию, новый архитектурный ансамбль.