Презентація на тему «Квадратні корені» (варіант 1)

Алмакаева 8-Б
Квадратні корені

Квадратний корінь
Квадратним коренем із числа a називається число, квадрат якого дорівнює a.Квадратний корінь із числа 0 дорівнює 0. Квадратного кореня з від'ємного числа не існує, оскільки квадрат будь-якого числа є невід'ємним.Квадратний корінь із додатного числа має два протилежних значення — додатне і від'ємне. Наприклад: і , тобто числа 3 і –3 є квадратними коренями з числа 9.Невід'ємне значення квадратного кореня називають арифметичним коренем

Квадратний корінь. Арифметичний квадратний корінь.
Рівняння х2 = а
Квадратним коренем із числа a називається число, квадрат якого дорівнює a.
Арифметичним квадратним коренем із числа a називається невід'ємне число, квадрат якого дорівнює a. Читаємо — «корінь квадратний з a».Знаком арифметичного квадратного кореня слугує радикал

Квадратний корінь. Арифметичний квадратний корінь.
Рівняння х2 = а
Квадратним коренем із числа a називається число, квадрат якого дорівнює a.
Арифметичним квадратним коренем із числа a називається невід'ємне число, квадрат якого дорівнює a. Читаємо — «корінь квадратний з a».Знаком арифметичного квадратного кореня слугує радикал

Пояснення
З давніх-давен поряд із відшукуванням площі квадрата за відомою довжиною його сторони доводилося розв'язувати обернену задачу: «Якою повинна бути сторона квадрата, щоб його площа дорівнювала а?» Таку задачу вміли розв'язувати ще 4 тисячі років тому вавилонські вчені. Вони складали таблиці квадратів чисел.Розв'яжемо задачу.Нехай довжина сторони квадрата дорівнює х, тоді його площа х2. Маємо рівняння х2= а.Щоб знайти корені цього рівняння, нам необхідно познайомитися з новими математичними поняттями.Якщо а = 49, то рівняння х2 = 49 має два корені 7 і -7.Дійсно, 72 = 49 і (-7)2 = 49. Яке з цих чисел задовольняє умові задачі? Відповідь: 7. Чому? (Довжина сторони є додатне число.)
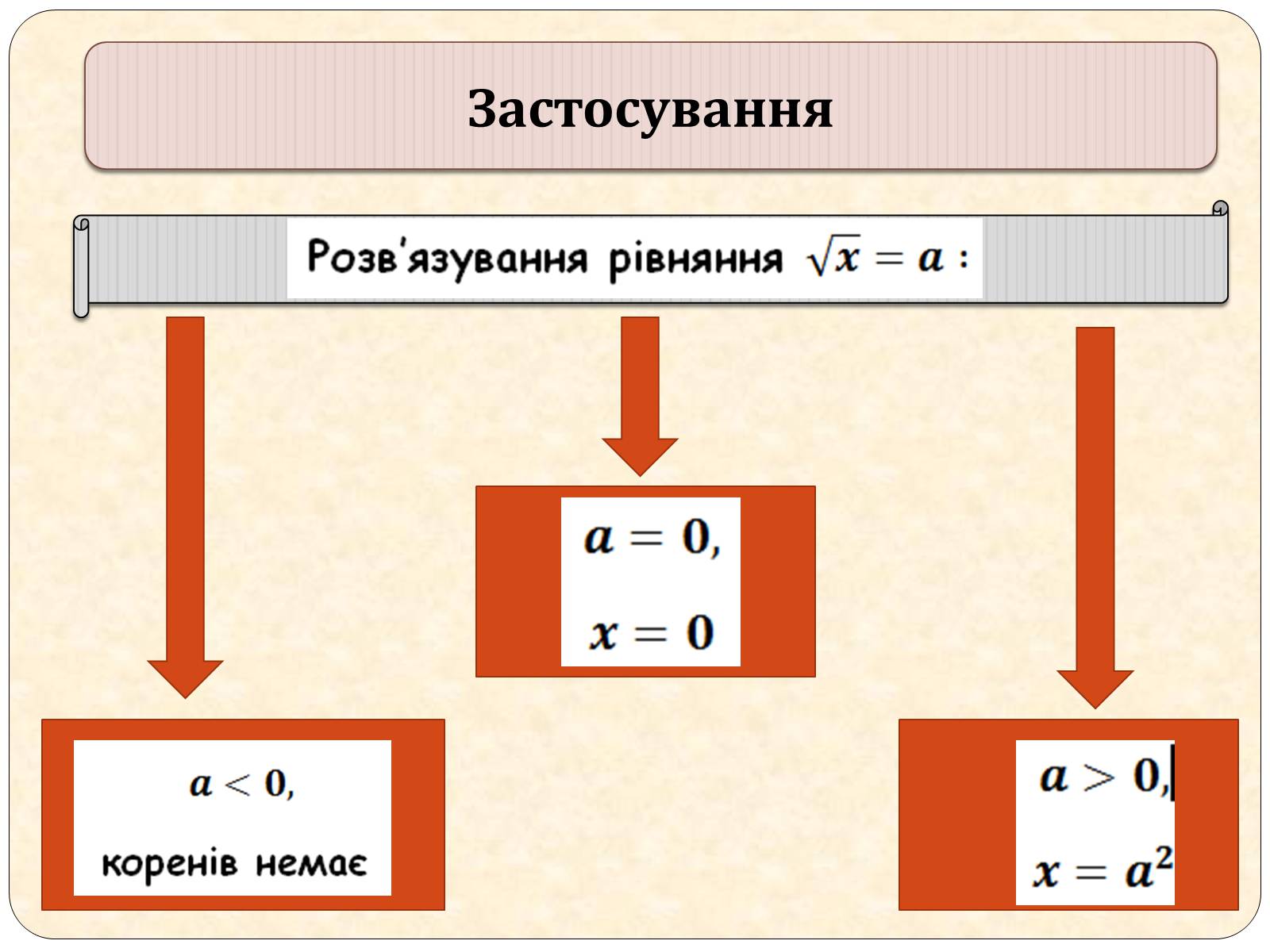
Застосування

Застосування

Приклади рішення рівнянь