Презентація на тему «Інтеграл»

МІНІ
ПІДРУЧНИК
Інтеграл та
його застосування
11КЛАС
Ананьєва
Поліна

Зміст
Означення
Таблиця невизначених інтегралів
Диференціювання та інтегрування
Властивість первісної
Правила знаходження
первісної
Криволінійна трапеція та
її площа
Визначений інтеграл
Формула
Ньютона - Лейбніца
Тести та завдання

Означення
Функція F(x) називається первісною для функції f(x) на даному проміжку, якщо для будь-якого х з цього проміжку
Перейти до змісту

Таблиця первісних (невизначених інтегралів)
Функція f(x)
Загальний вигляд первісних F(x)+С, де С - стала
Запис за допомогою невизначеного інтеграла
С
1
х+С
Перейти до змісту

Операція знаходження
Похідної функції-
диференціювання
Первісної функції-
інтегрування
Диференціювання функції f(x) – операція знаходження її похідної .
Наприклад. Знайти похідну функції:
а) ; б) .
Розв'язання
а) ;
б) .
Знаходження функції f(x) за даною її похідною F(x) називається операцією інтегрування.
Операція інтегрування обернена до операції диференціювання.
Наприклад.
а) Якщо , то , оскільки .
б) Якщо , то ,
оскільки .
Перейти до змісту
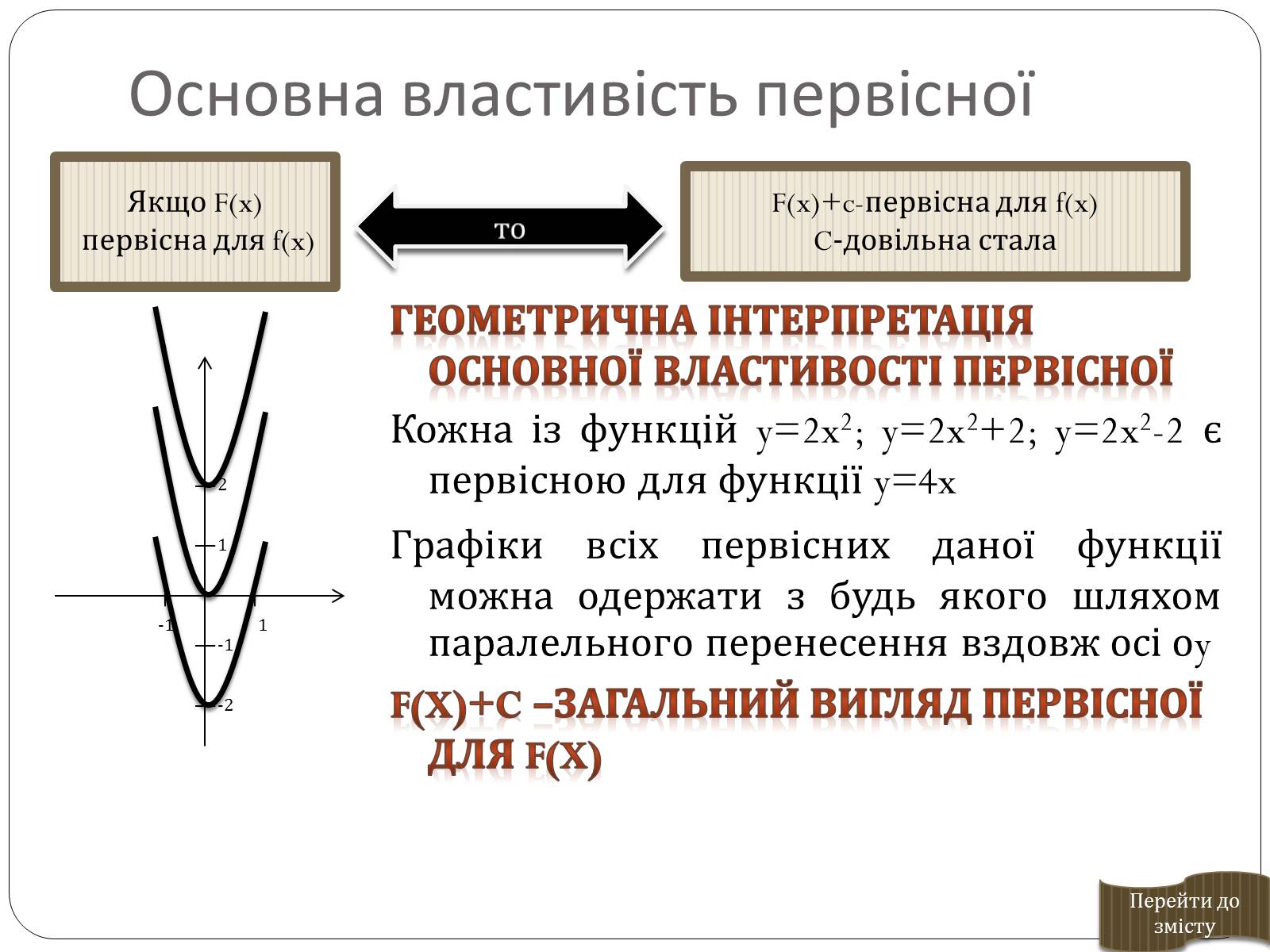
Якщо F(x)
первісна для f(x)
Основна властивість первісної
Геометрична інтерпретація основної властивості первісної
Кожна із функцій y=2x2; y=2x2+2; y=2x2-2 є первісною для функції y=4x
Графіки всіх первісних даної функції можна одержати з будь якого шляхом паралельного перенесення вздовж осі оy
F(x)+c –загальний вигляд первісної для f(x)
то
F(x)+c-первісна для f(x)
C-довільна стала
1
2
-1
-2
-1
1
Перейти до змісту
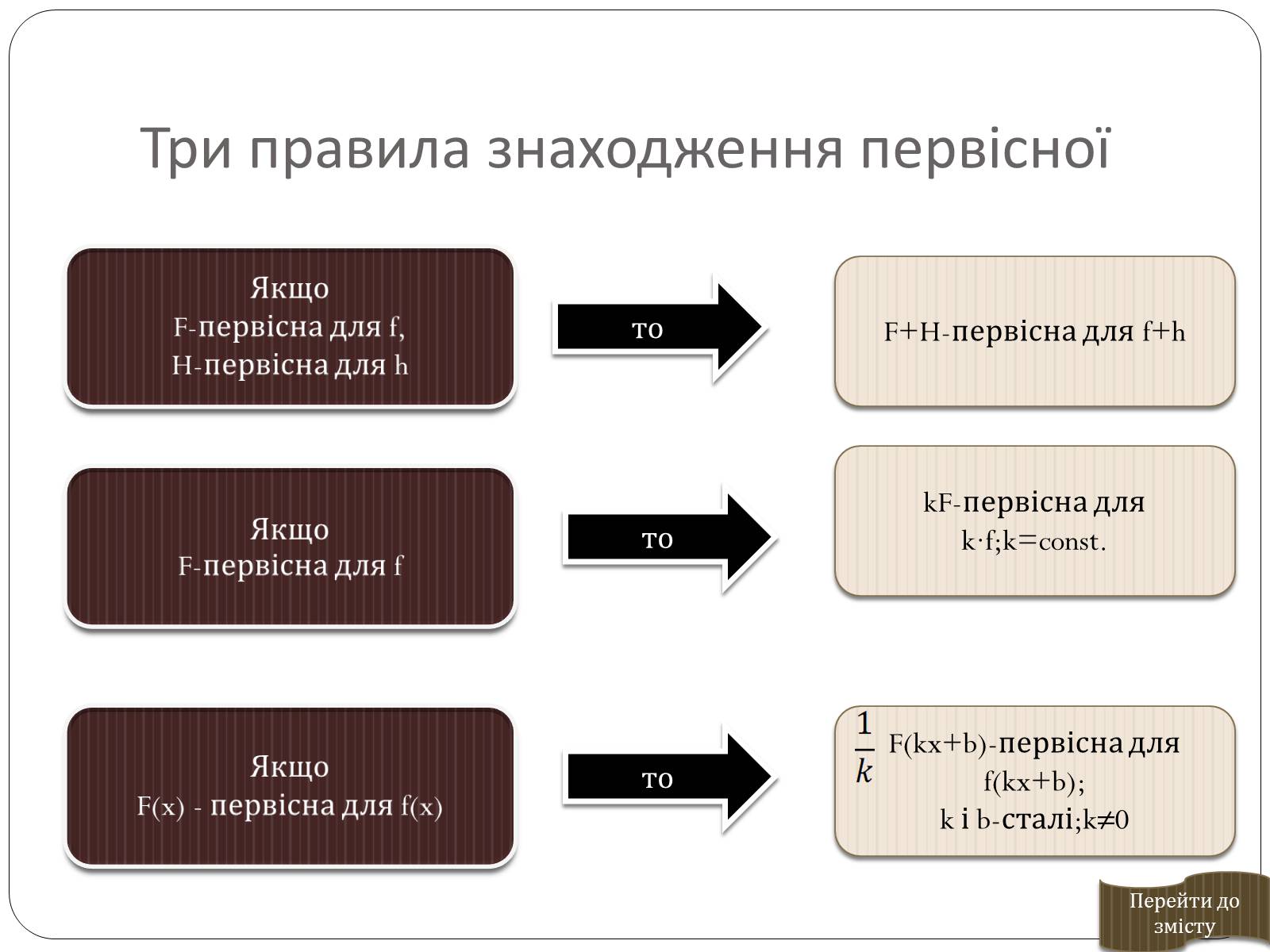
Три правила знаходження первісної
Якщо
F-первісна для f,
H-первісна для h
Якщо
F-первісна для f
Якщо
F(x) - первісна для f(x)
то
то
то
F+H-первісна для f+h
kF-первісна для k∙f;k=const.
F(kx+b)-первісна для f(kx+b);
k і b-сталі;k≠0
Перейти до змісту
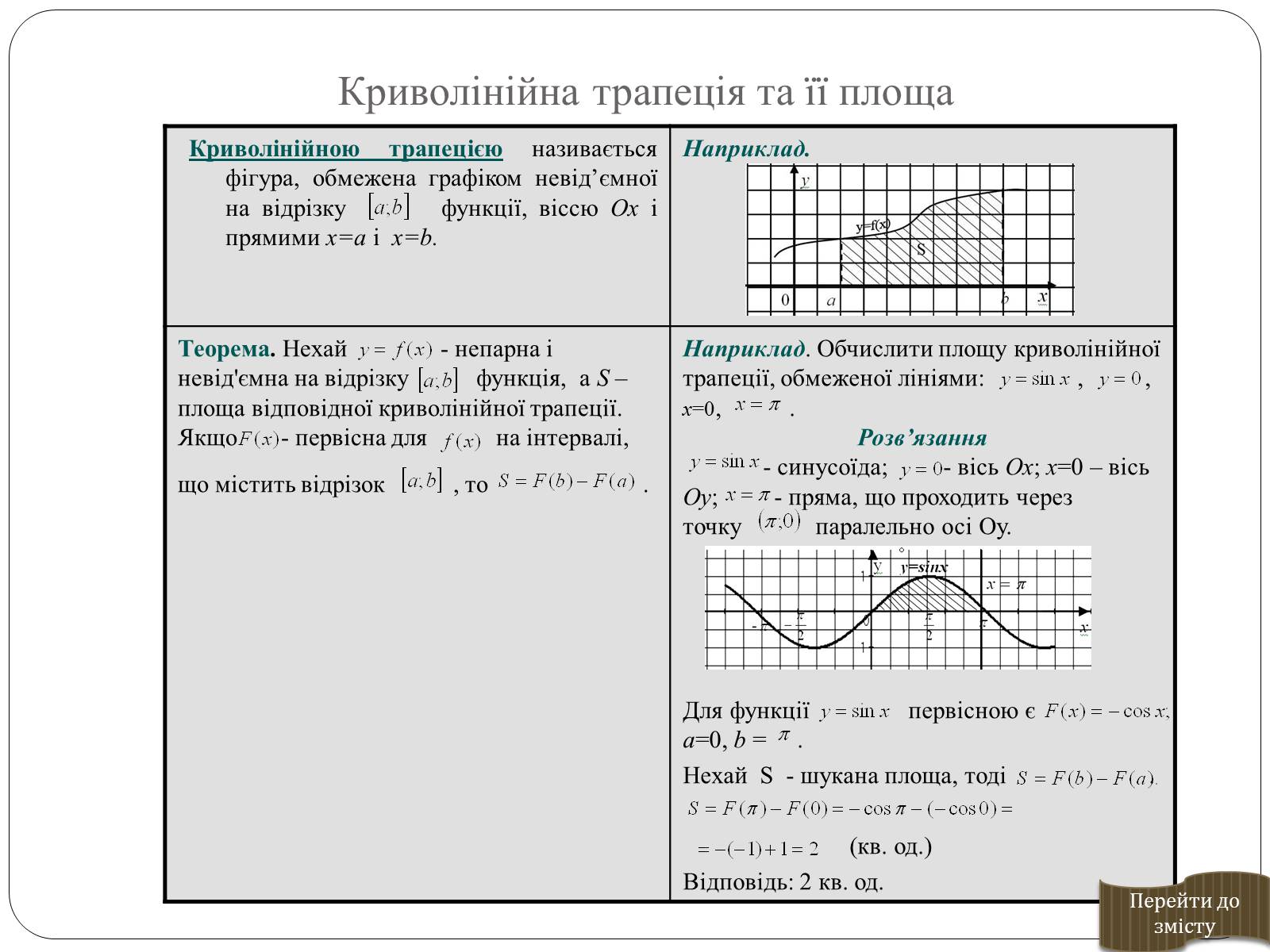
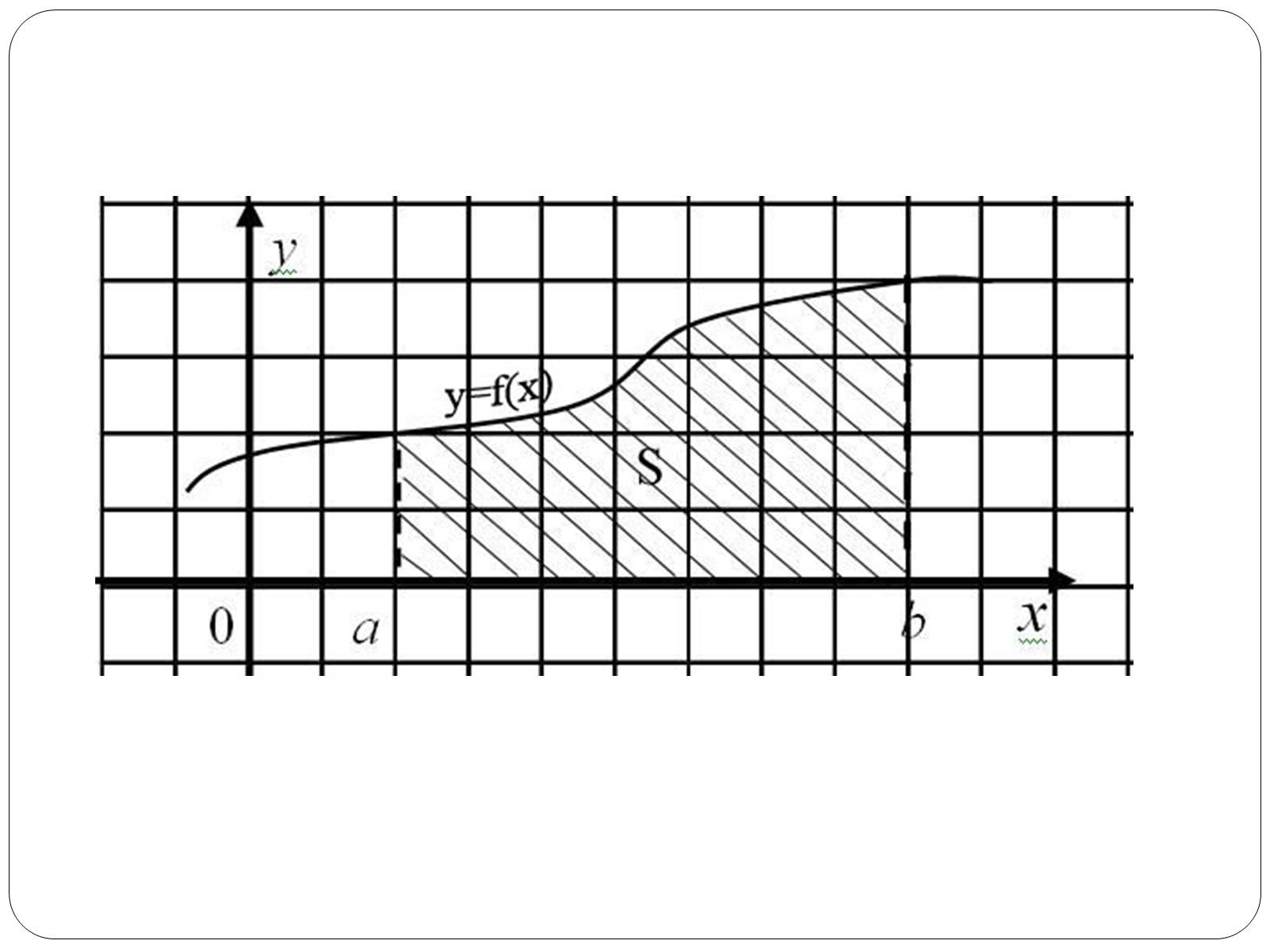
Криволінійна трапеція та її площа
Криволінійною трапецією називається фігура, обмежена графіком невід'ємної на відрізку функції, віссю Ох і прямими x=a і x=b.
Наприклад.
Теорема. Нехай - непарна і невід'ємна на відрізку функція, а S – площа відповідної криволінійної трапеції.
Якщо - первісна для на інтервалі, що містить відрізок , то .
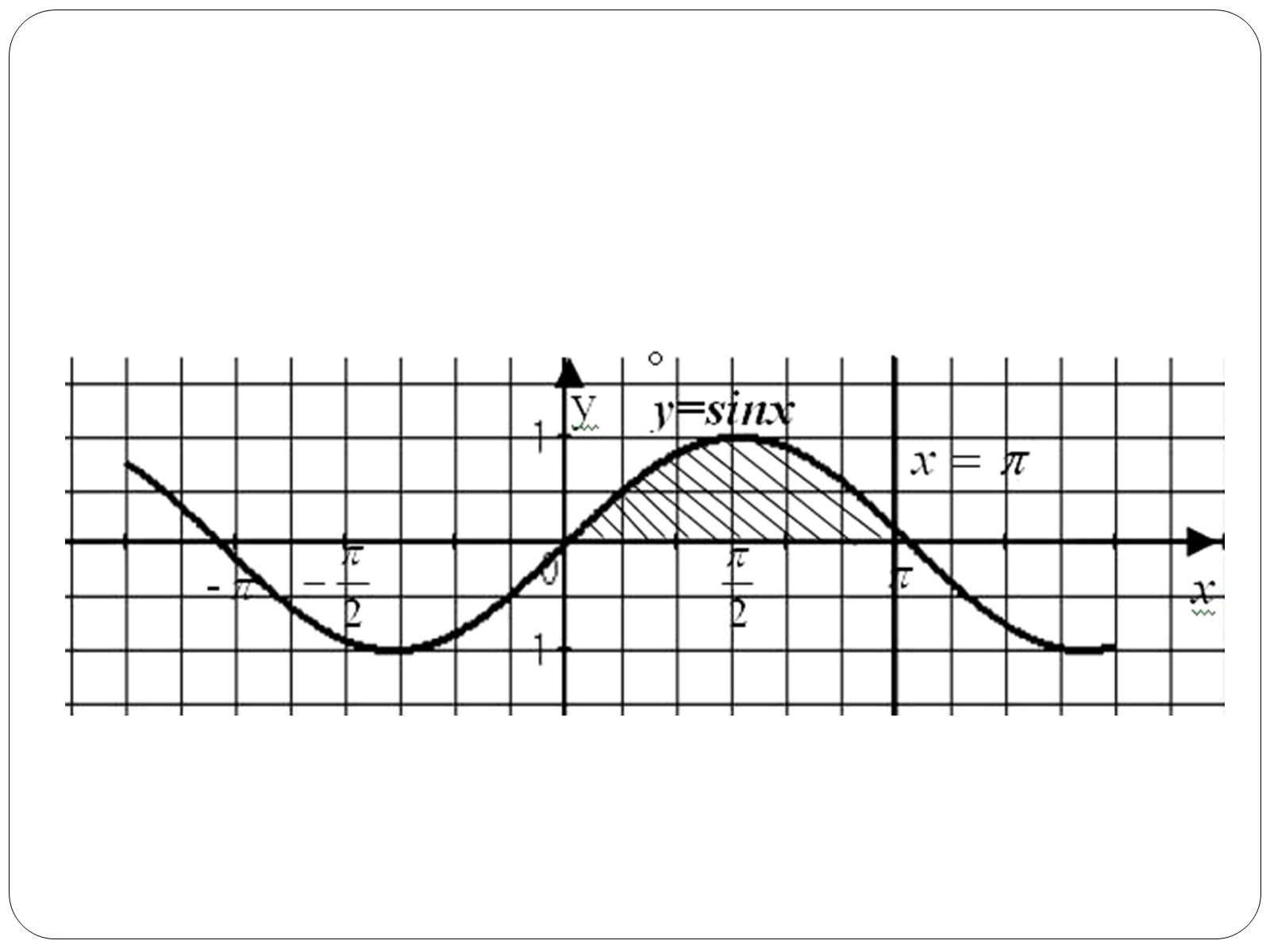
Наприклад. Обчислити площу криволінійної трапеції, обмеженої лініями: , , x=0, .
Розв'язання
- синусоїда; - вісь Ox; x=0 – вісь Оу; - пряма, що проходить через
точку паралельно осі Оу.
Для функції первісною є a=0, b = .
Нехай S - шукана площа, тоді .
(кв. од.)
Відповідь: 2 кв. од.
Перейти до змісту

Площа криволінійної трапеції
S – площа криволінійної трапеції;
F (x) – будь-яка первісна функції f(x) на відрізку
[a; b].
Площу S криволінійної трапеції, обмеженої графіком функції y=f(x) і прямими y=0, x=a i x=b (a
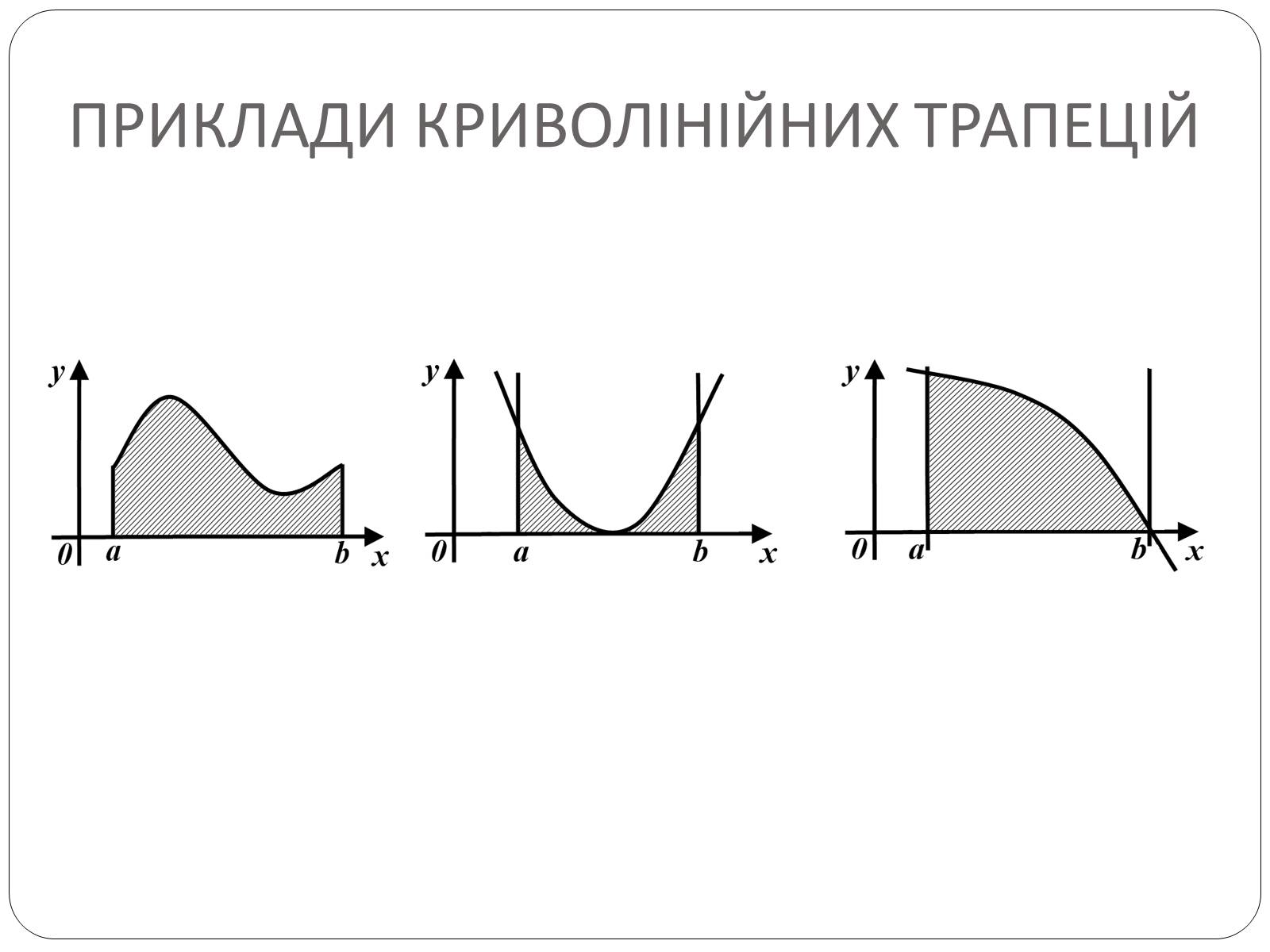
Приклади криволінійних трапецій
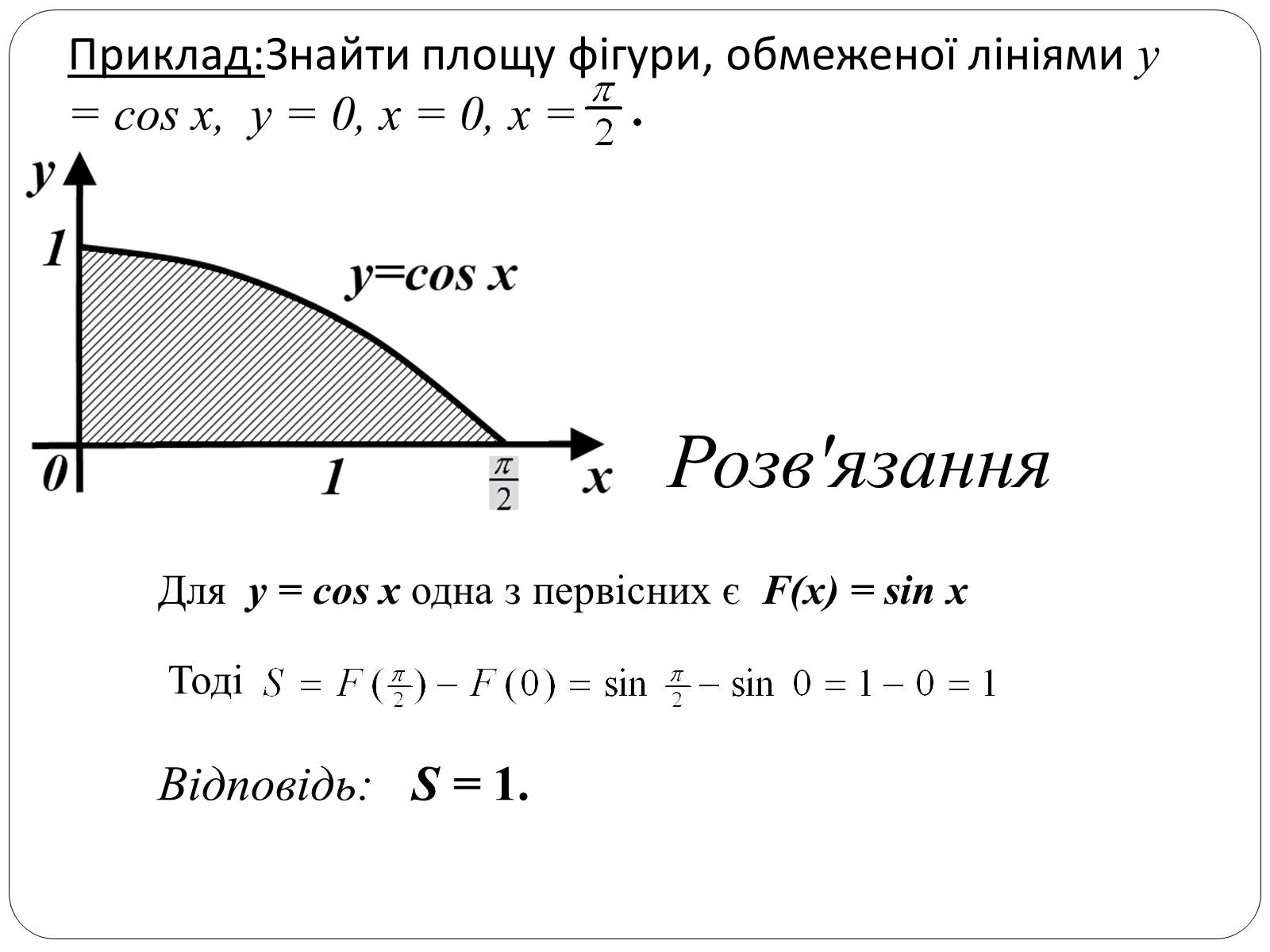
Приклад:Знайти площу фігури, обмеженої лініями y = cos x, y = 0, x = 0, x =
Розв'язання
Для y = cos x одна з первісних є F(x) = sin x
Тоді
Відповідь: S = 1.
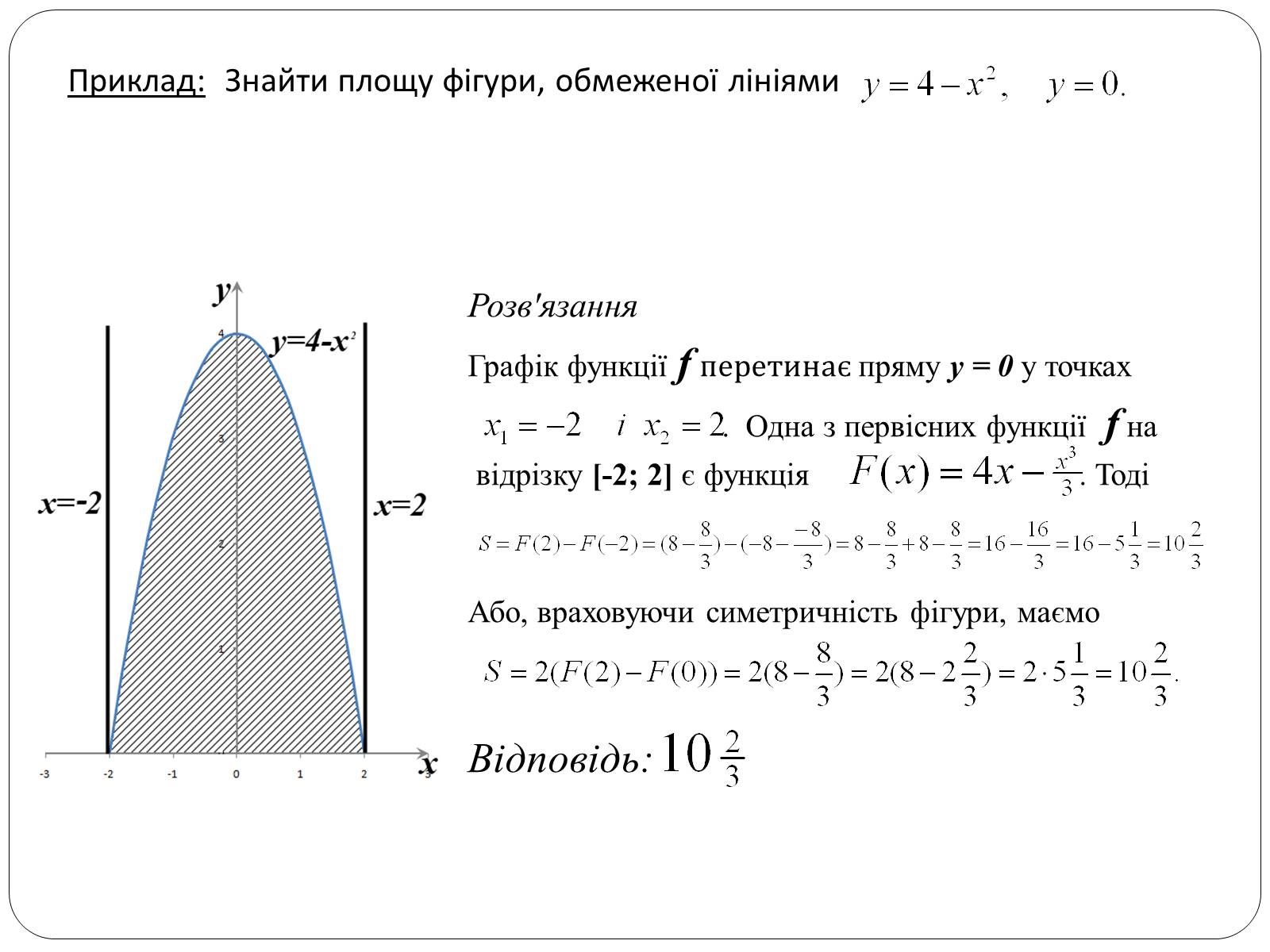
Приклад: Знайти площу фігури, обмеженої лініями
Розв'язання
Графік функції f перетинає пряму y = 0 у точках
. Одна з первісних функції f на
відрізку [-2; 2] є функція tt . Тоді
Або, враховуючи симетричність фігури, маємо
Відповідь:
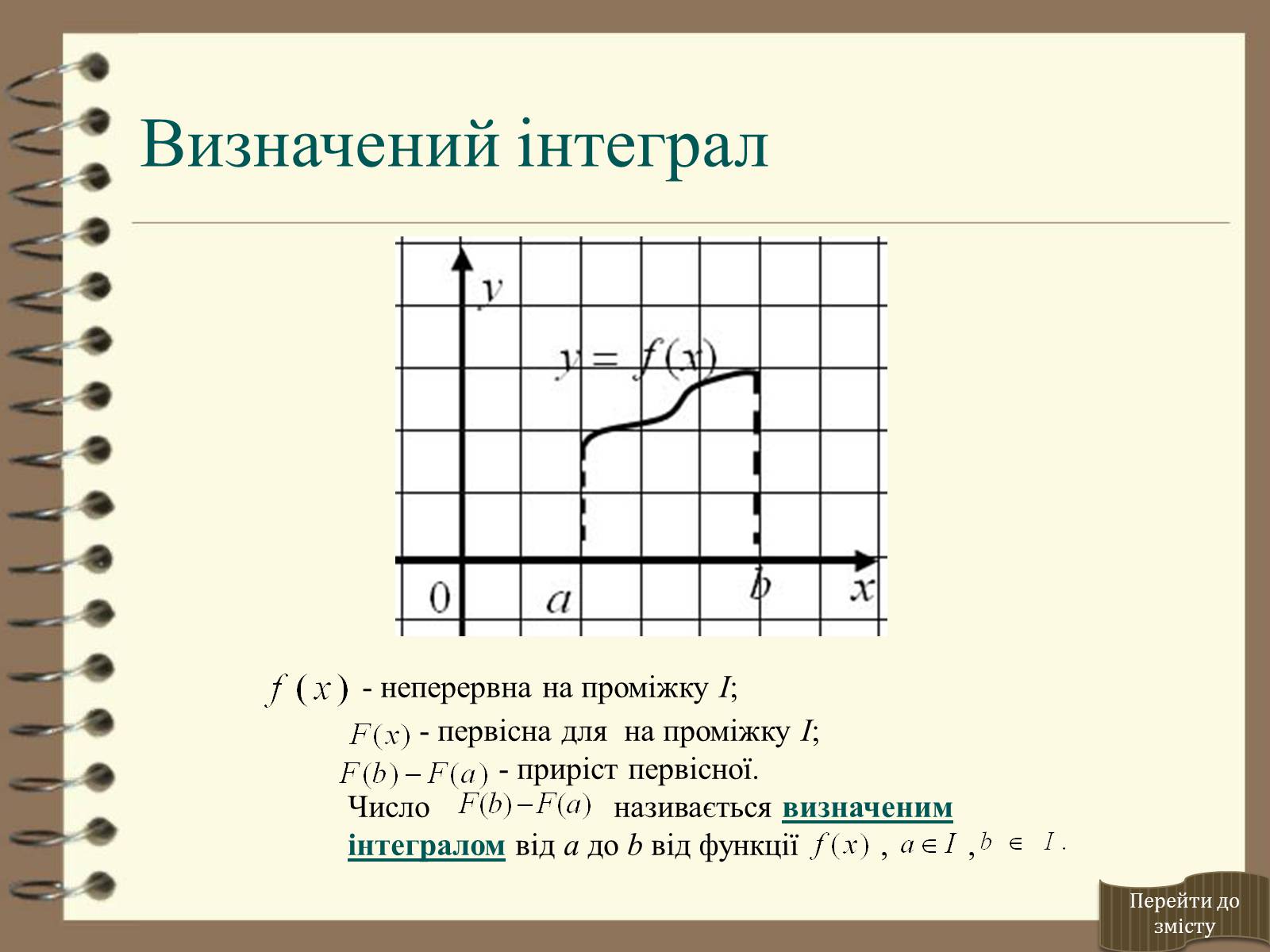
Визначений інтеграл
- неперервна на проміжку І;
- первісна для на проміжку І;
- приріст первісної.
Число називається визначеним інтегралом від a до b від функції , ,
Перейти до змісту
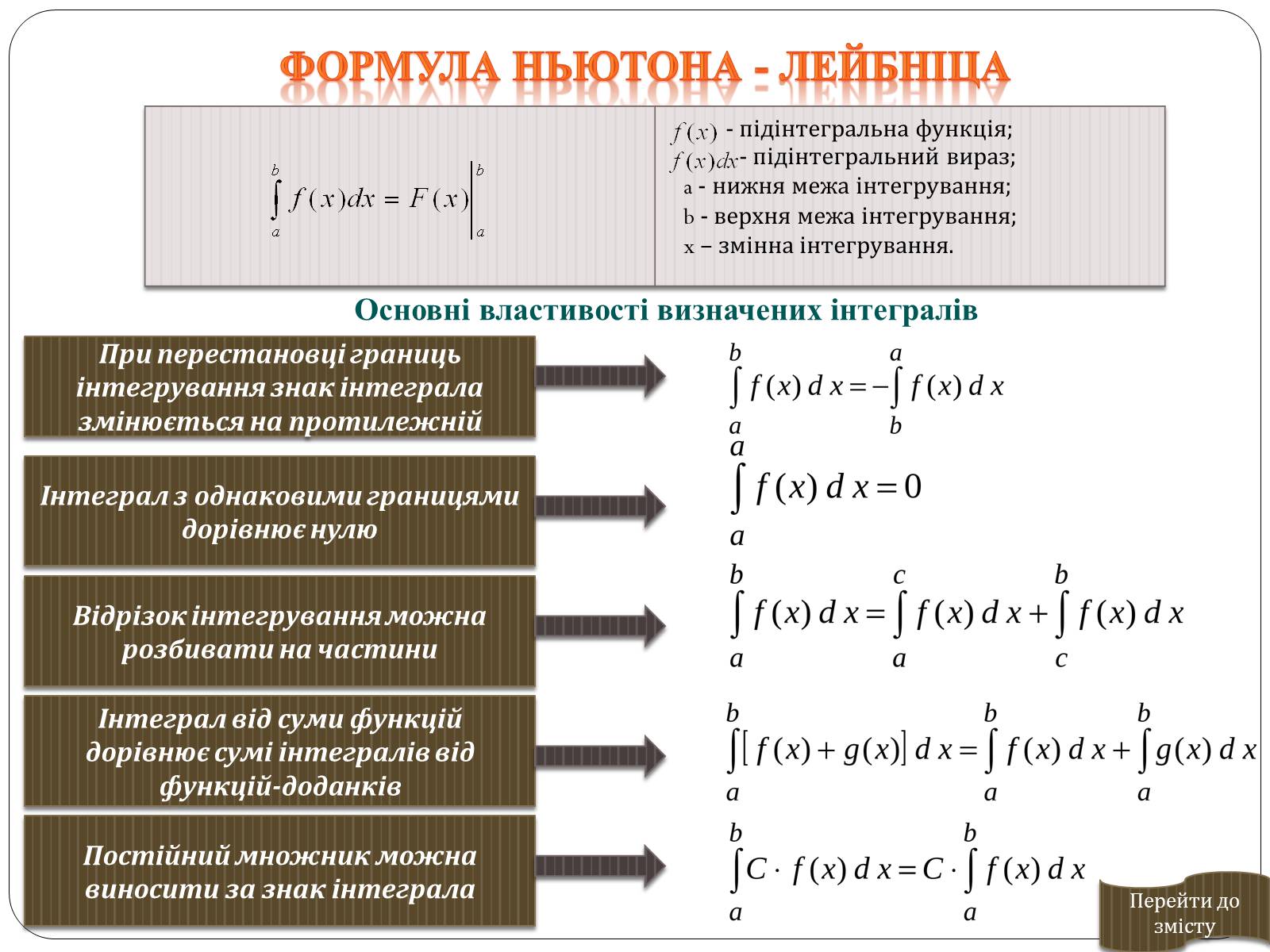
Формула Ньютона - Лейбніца
- підінтегральна функція;
- підінтегральний вираз;
a - нижня межа інтегрування;
b - верхня межа інтегрування;
x – змінна інтегрування.
Основні властивості визначених інтегралів
При перестановці границь інтегрування знак інтеграла змінюється на протилежній
Інтеграл з однаковими границями дорівнює нулю
Відрізок інтегрування можна розбивати на частини
Інтеграл від суми функцій дорівнює сумі інтегралів від функцій-доданків
Постійний множник можна виносити за знак інтеграла
Перейти до змісту

1. 1.
А Б В А Б В
2. 2.
А Б В А Б В
3. 3.
А Б В А Б В
ВАРІАНТ І
ВАРІАНТ ІІ
Тестові завдання
Перейти до змісту

4. 4.
А Б В А Б В
5. 5.
А Б В А Б В
ВАРІАНТ І
ВАРІАНТ ІІ
Тестові завдання
Відповіді
Перейти до змісту

Завдання
1. Знайти загальний вигляд первісної для функції:
2. Для функції знайти первісну, графік
якої проходить через точку А:
А(-1;-3);
А(1;2);
Відповіді
А
А
Б
Б
А
А
ВАРІАНТ І
ВАРІАНТ ІІ
Перейти до змісту

3. Обчислити інтеграл:
Відповіді
А
А
Б
Б
ВАРІАНТ ІІ
ВАРІАНТ І
Перейти до змісту
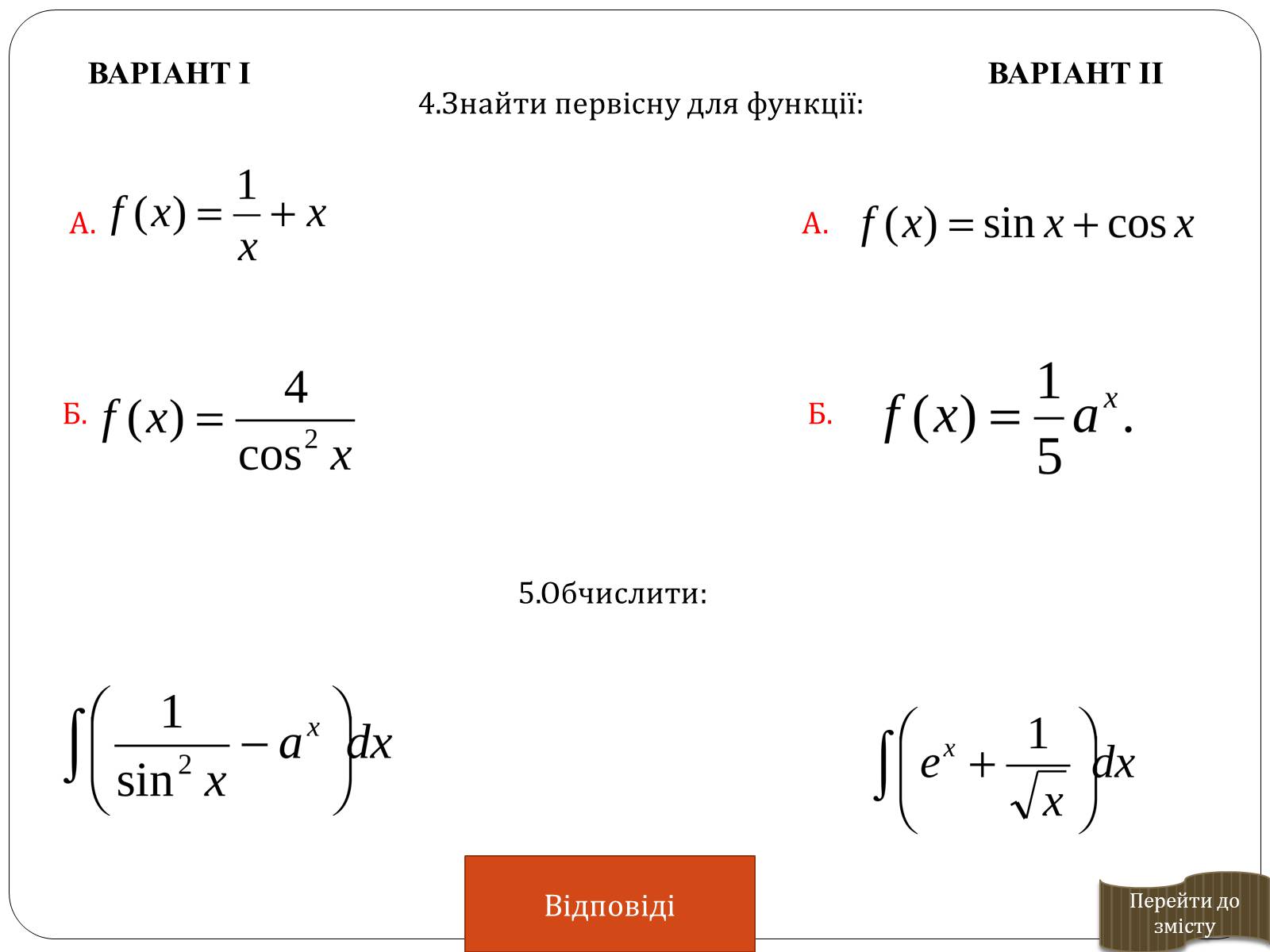
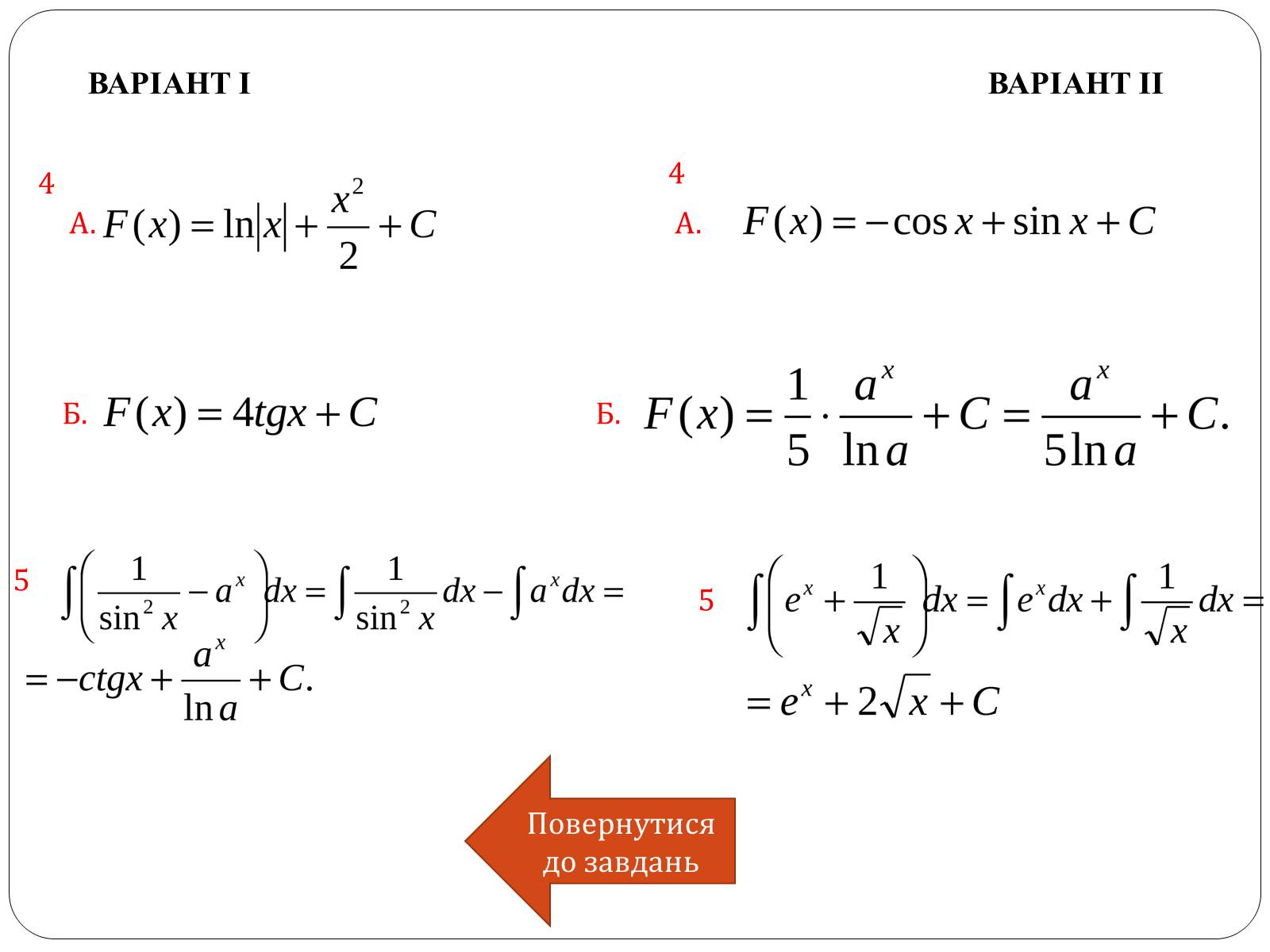
4.Знайти первісну для функції:
ВАРІАНТ ІІ
ВАРІАНТ І
5.Обчислити:
А. А.
Б. Б.
Відповіді
Перейти до змісту

6.Обчисліть площу криволінійної трапеції, обчисленої графіком функції f(х) = х3 та прямими у = 0; х = 1; х = 2.
ВАРІАНТ ІІ
ВАРІАНТ І
6.Обчисліть площу криволінійної трапеції обмеженої графіком функції f(x) = sin х та прямими
Відповіді
Перейти до змісту

Дякую за увагу!
Перейти до змісту
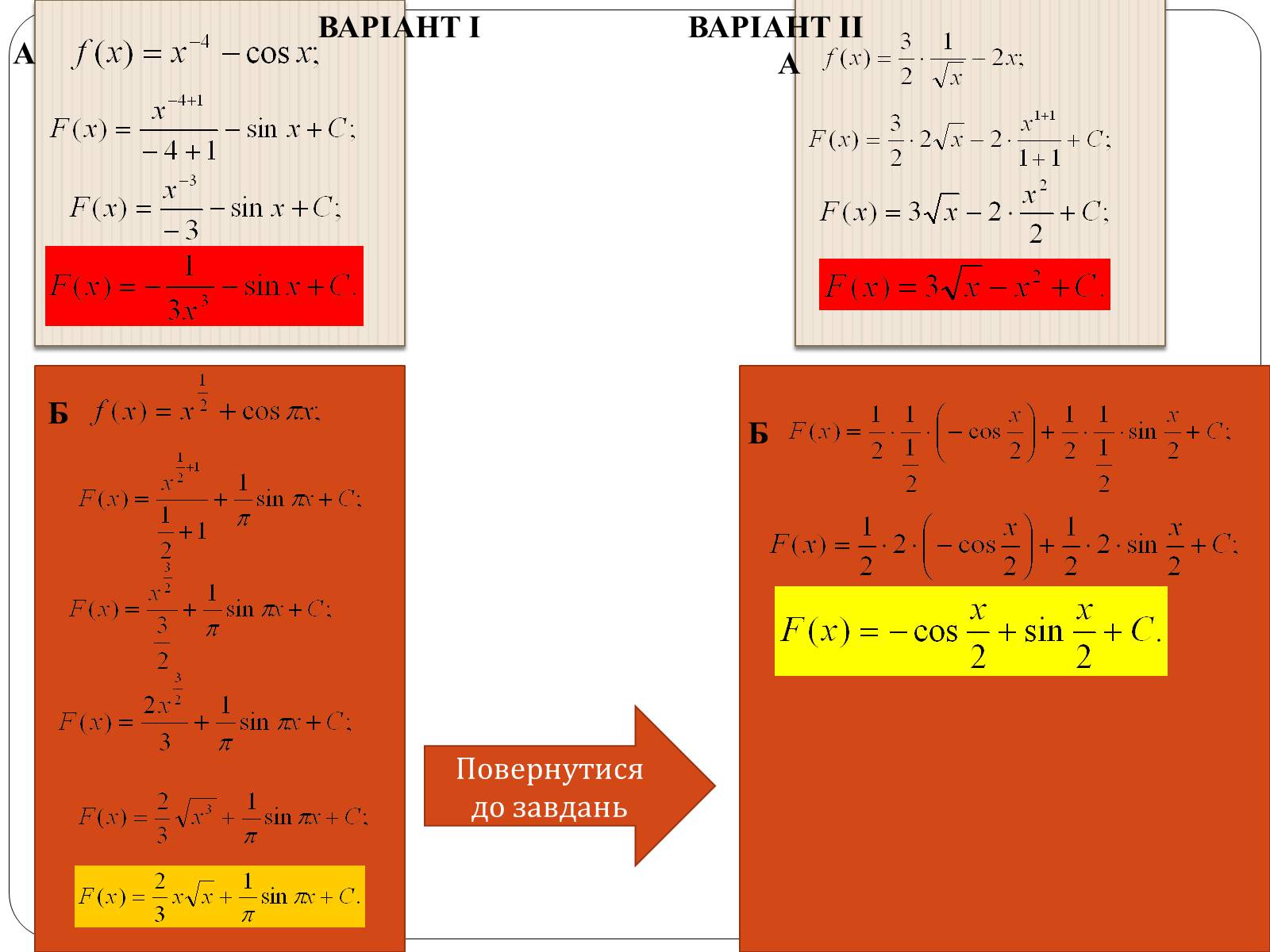
ВАРІАНТ І
ВАРІАНТ ІІ
А
А
Б
Б
Повернутися до завдань

А(-1;3);
С=-6
А(1;2);
С=4
повернутися до завдань
ВАРІАНТ І
ВАРІАНТ ІІ
А
А
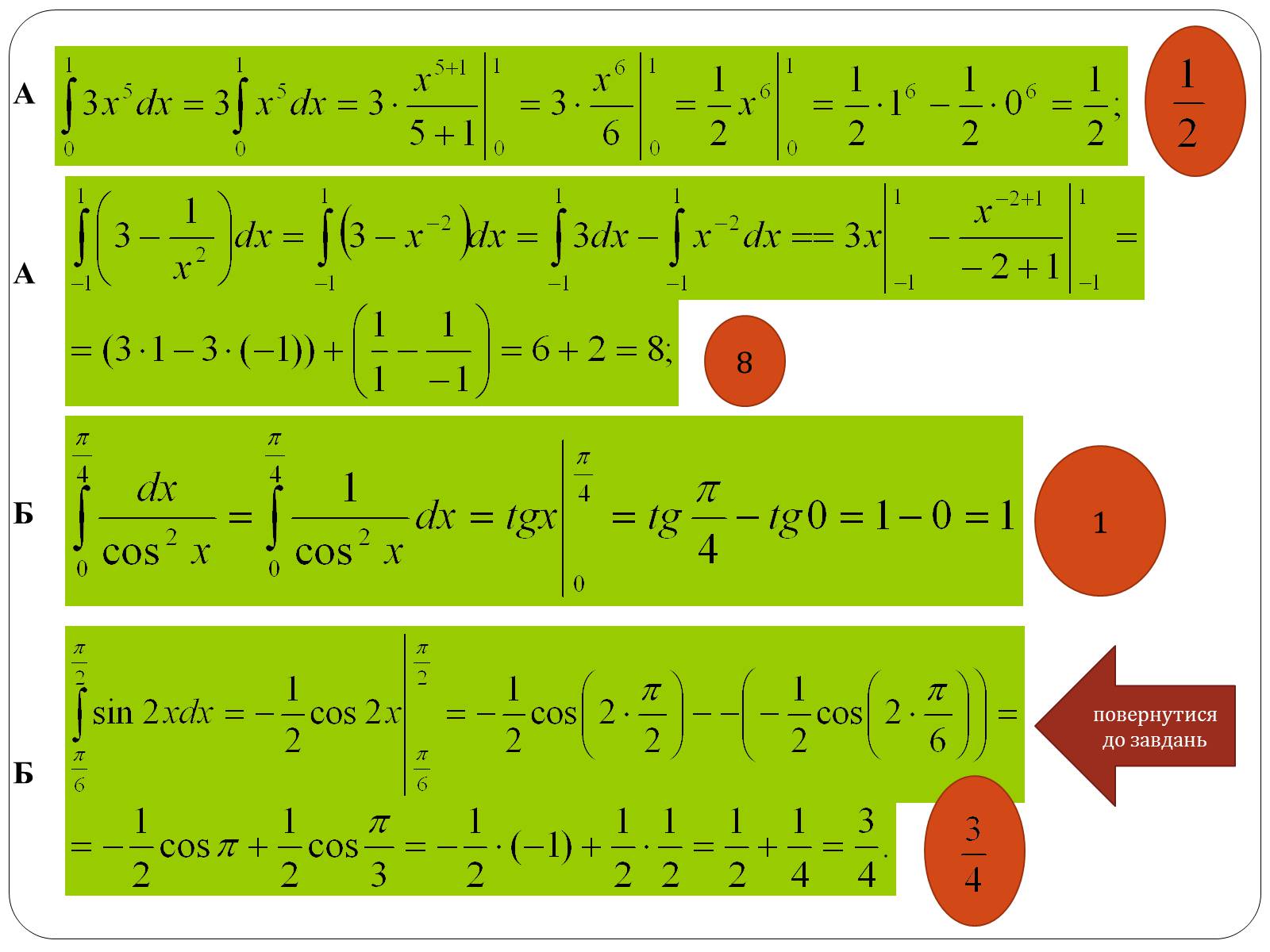
8
1
повернутися до завдань
А
А
Б
Б
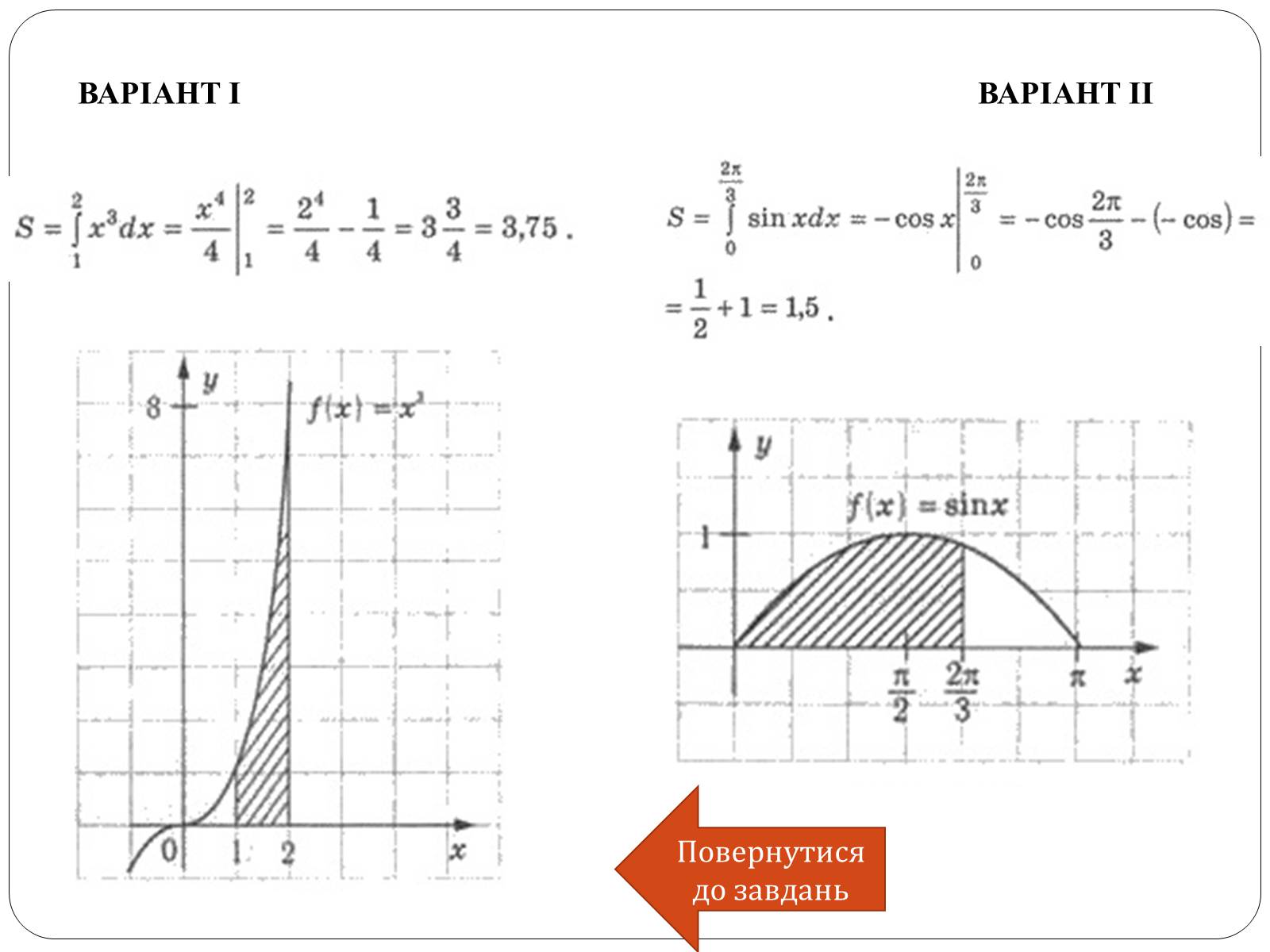
ВАРІАНТ ІІ
ВАРІАНТ І
Повернутися до завдань
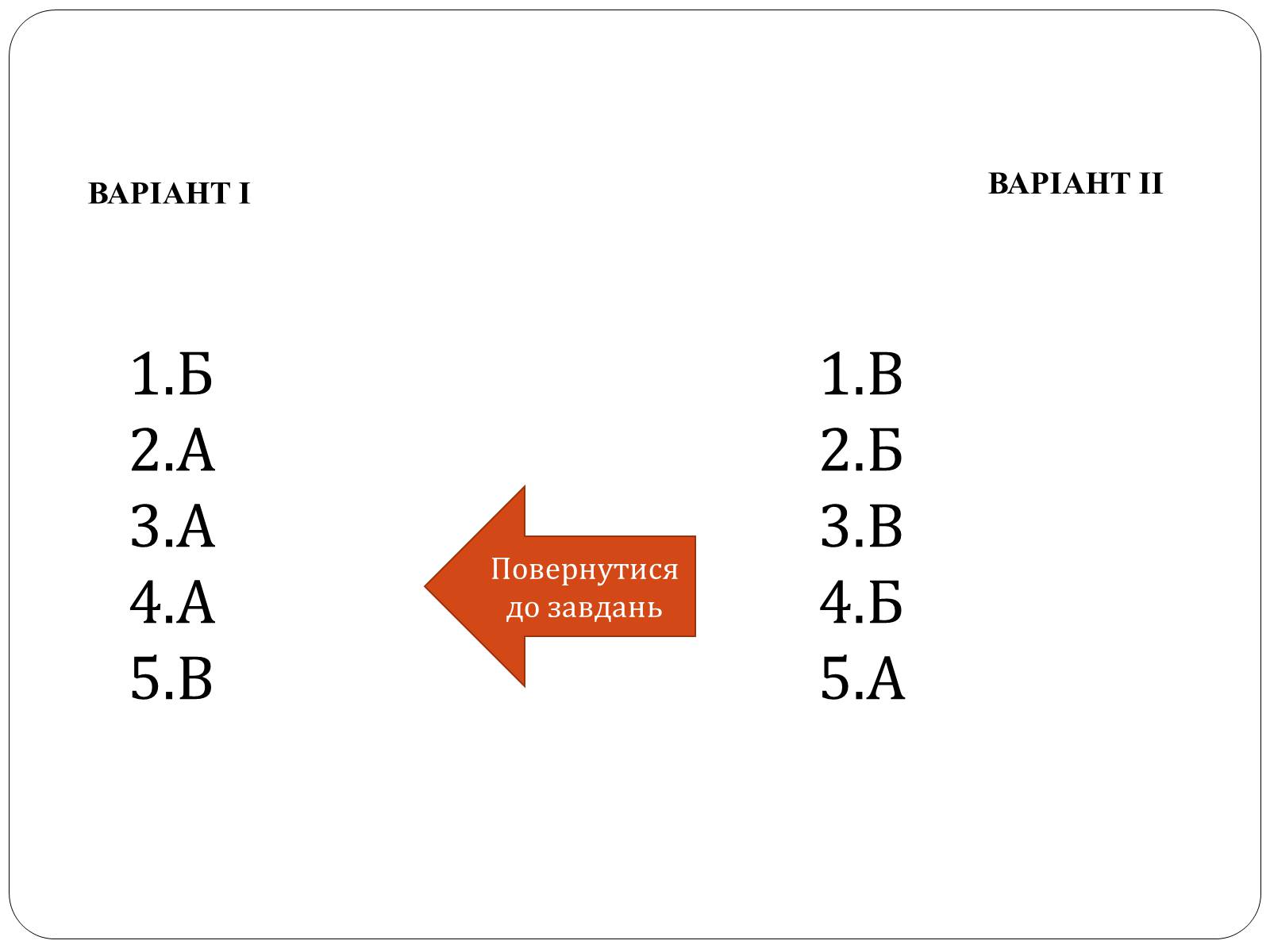
ВАРІАНТ І
ВАРІАНТ ІІ
Б
А
А
А
В
В
Б
В
Б
А
Повернутися до завдань
А. А.
Б. Б.
ВАРІАНТ І
ВАРІАНТ ІІ
4
4
5
5
Повернутися до завдань
А. А.
Б. Б.
ВАРІАНТ І
ВАРІАНТ ІІ
4
4
5
5
Повернутися до завдань
А. А.
Б. Б.
ВАРІАНТ І
ВАРІАНТ ІІ
4
4
5
5
Повернутися до завдань

Не вірно
Повернутися до завдань

Правильна відповідь
Поернутися до завдань

Правильна відповідь
Повернутися до завдань

Не вірно
Повернутися до завдань