Презентація на тему «Дотична»
Слайд #1

Задача №2
Дотична
Слайд #2

Умова задачі
Знайти спільну дотичну пряму для кривих х2+y2=2013 і ху=2013
Слайд #3

Функції не мають спільних точок
Слайд #4
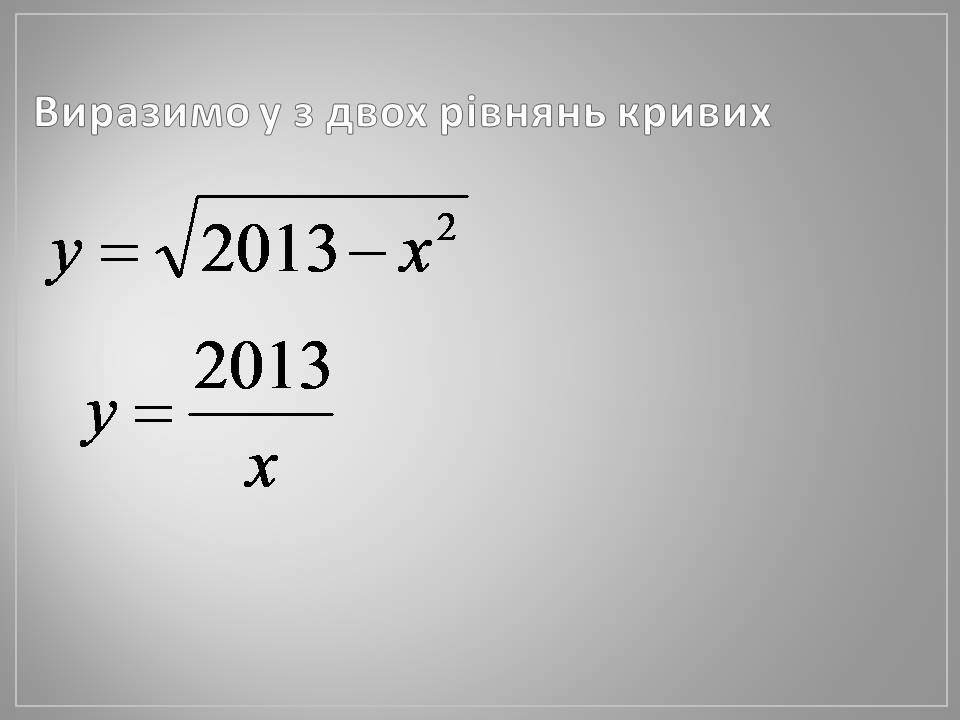
Виразимо у з двох рівнянь кривих
Слайд #5
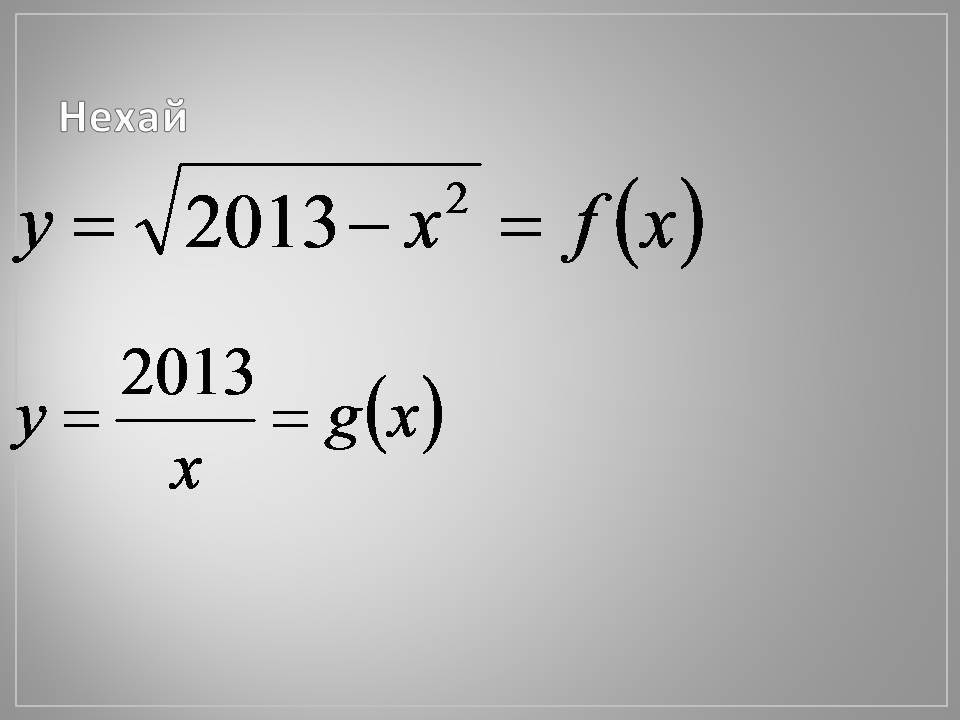
Нехай
Слайд #6
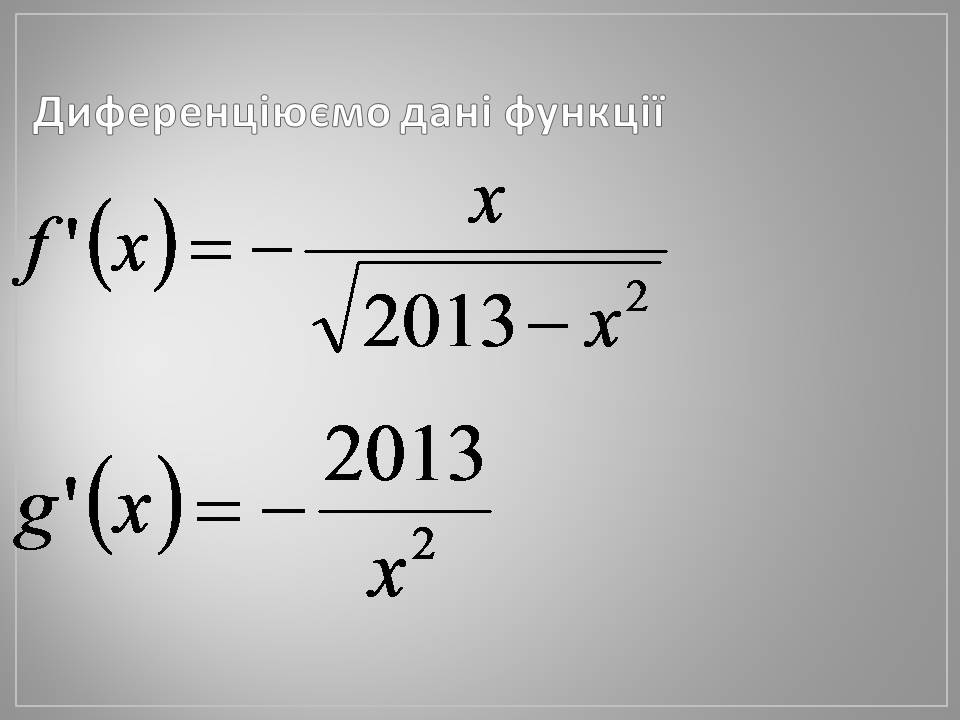
Диференціюємо дані функції
Слайд #7
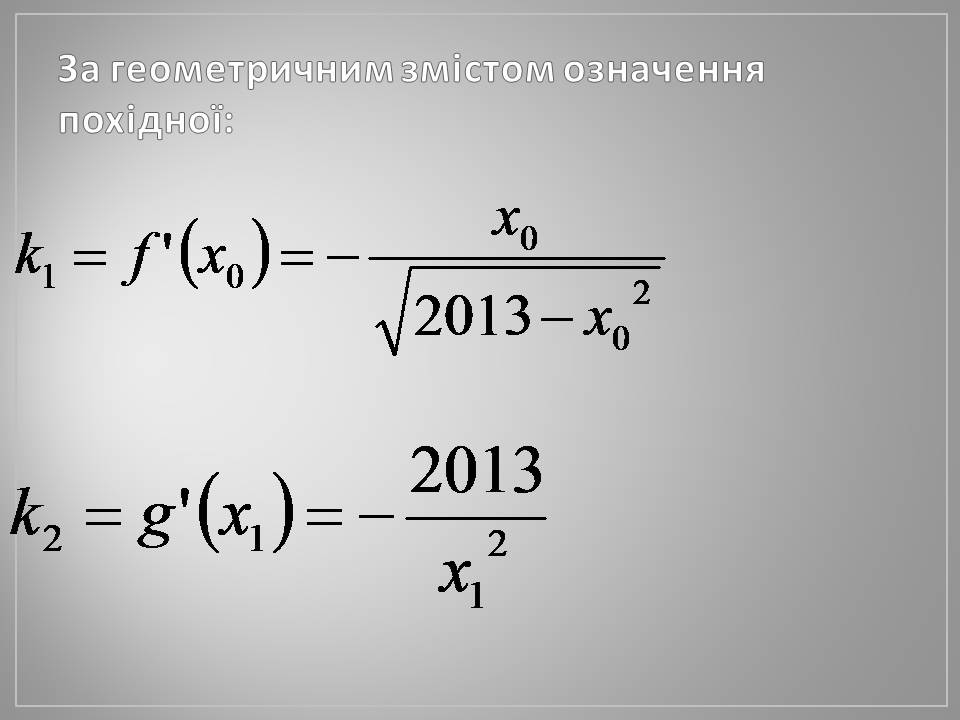
За геометричним змістом означення похідної:
Слайд #8
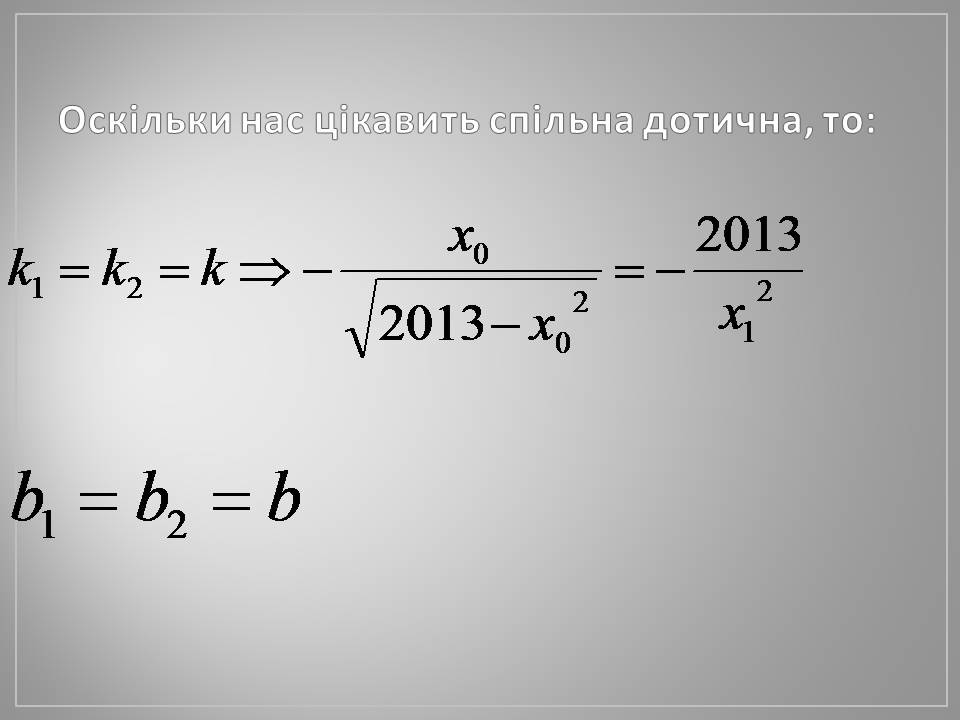
Оскільки нас цікавить спільна дотична, то:
Слайд #9
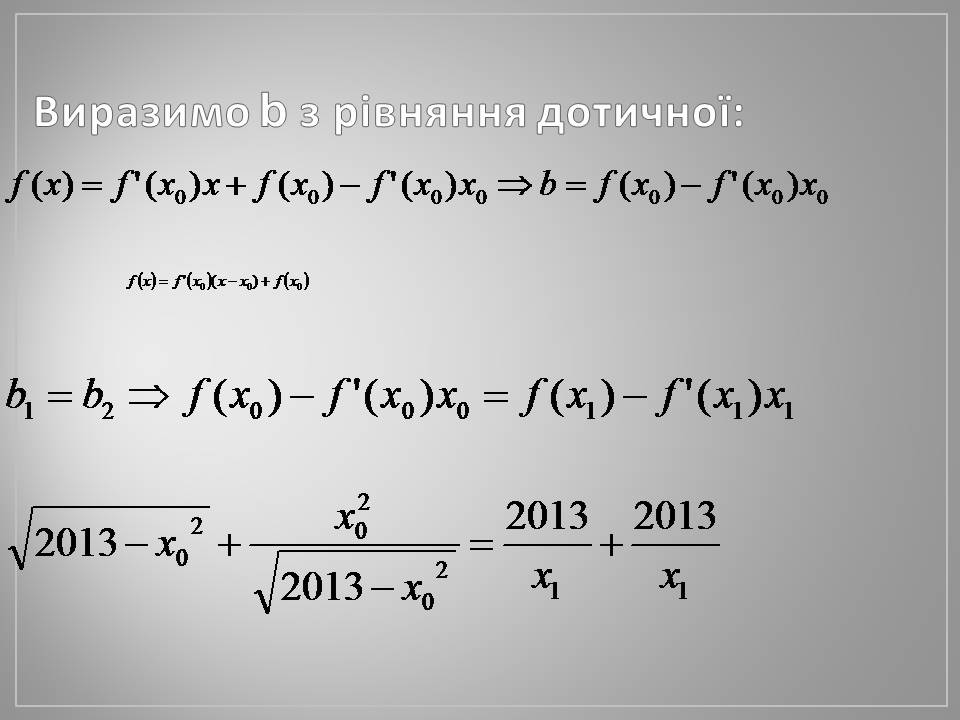
Виразимо b з рівняння дотичної:
Слайд #10
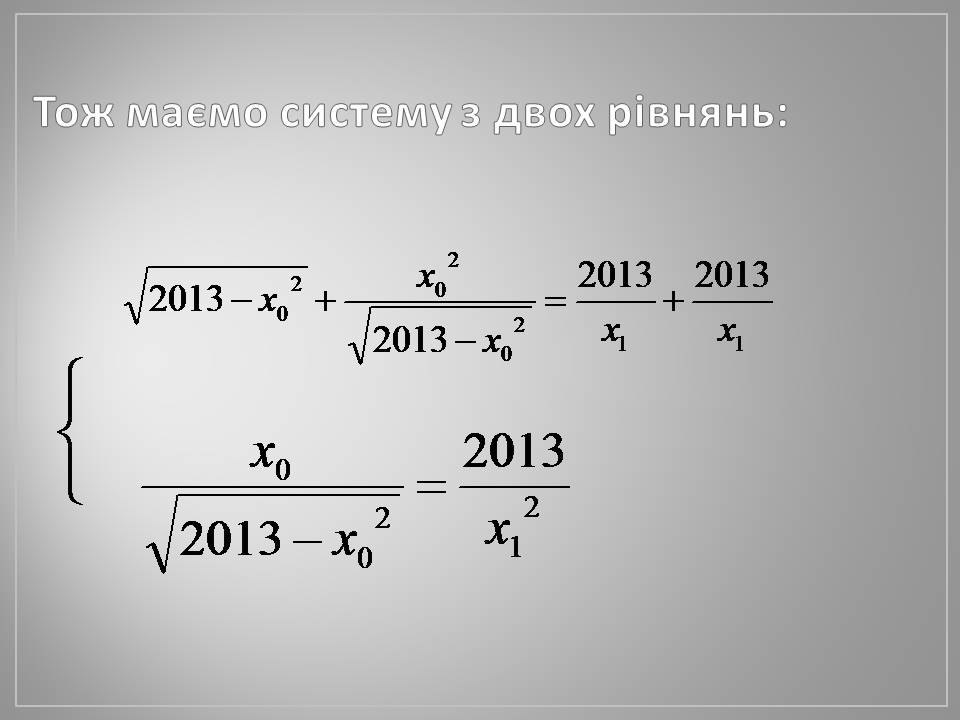
Тож маємо систему з двох рівнянь:
Слайд #11
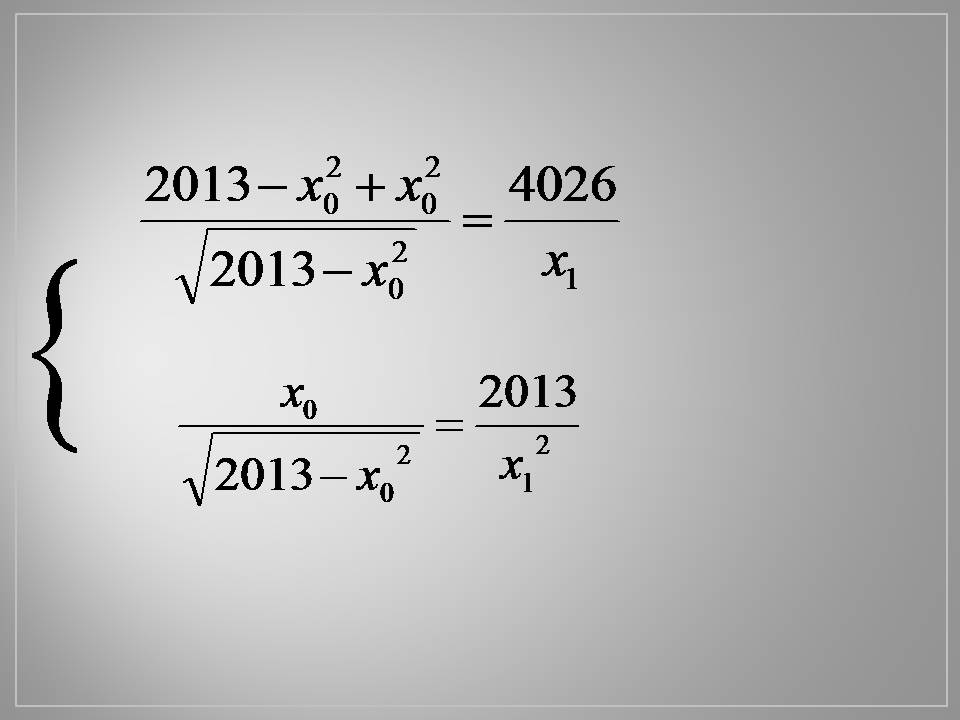
Тож маємо систему з двох рівнянь:
Слайд #12
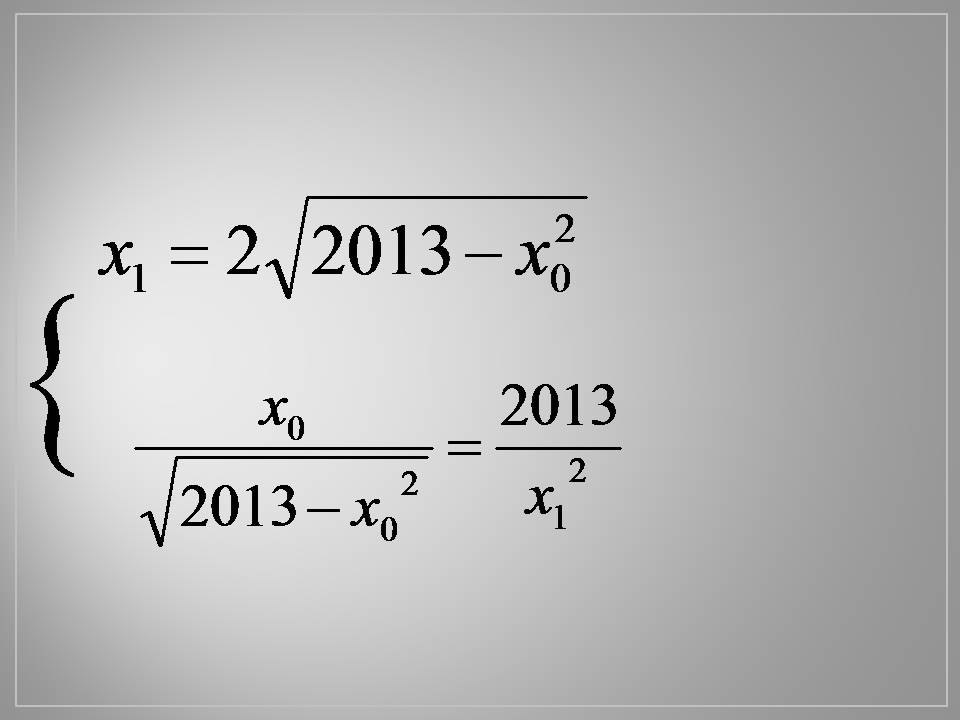
Тож маємо систему з двох рівнянь:
Слайд #13
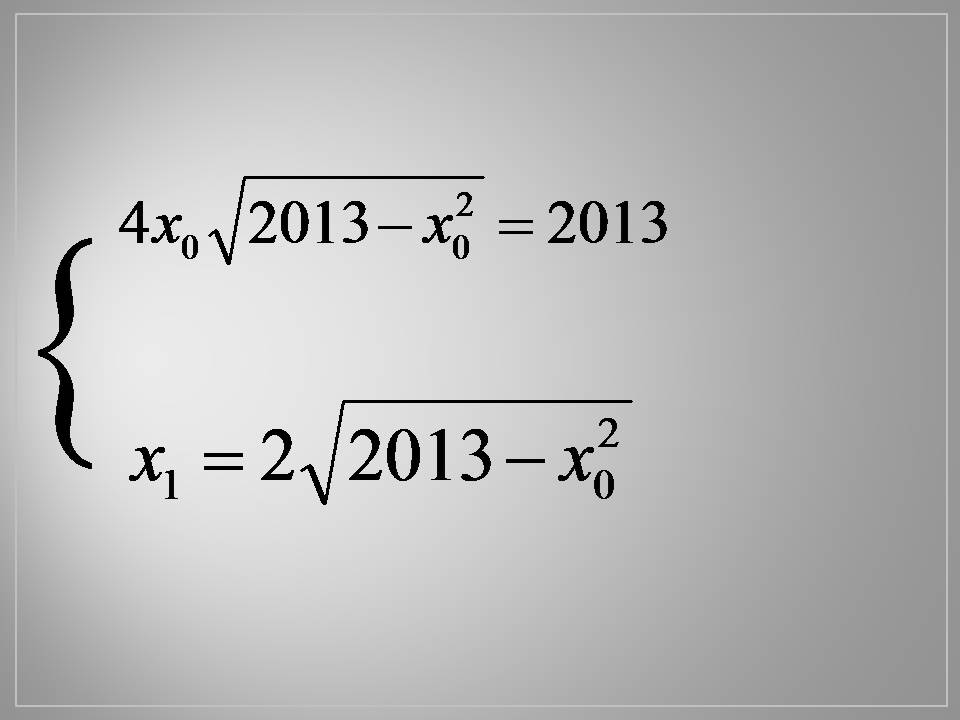
Тож маємо систему з двох рівнянь:
Слайд #14
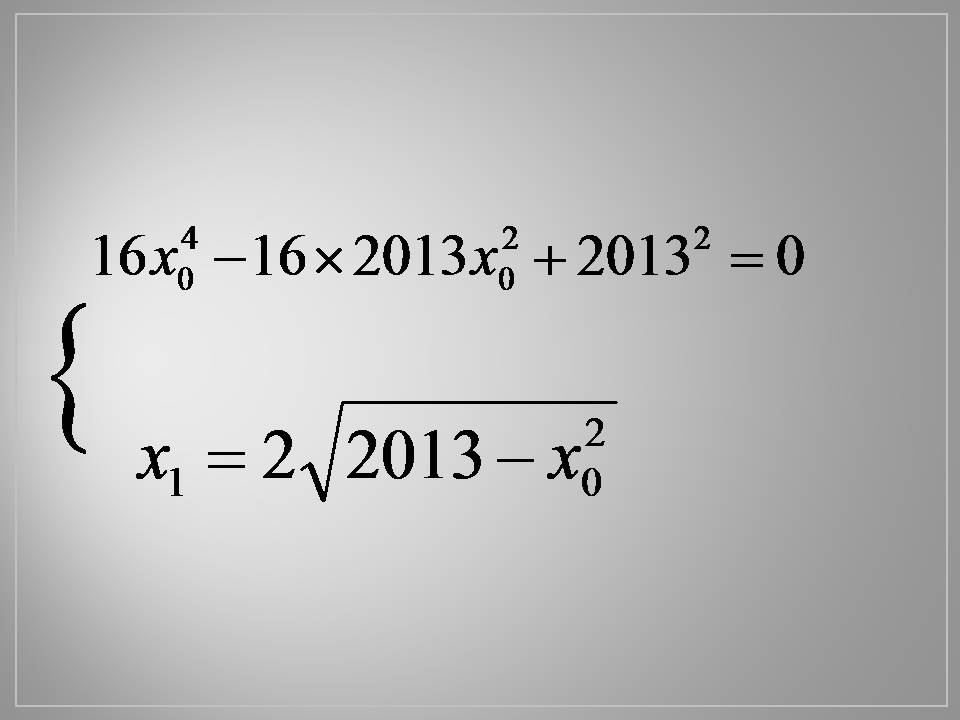
Тож маємо систему з двох рівнянь:
Слайд #15
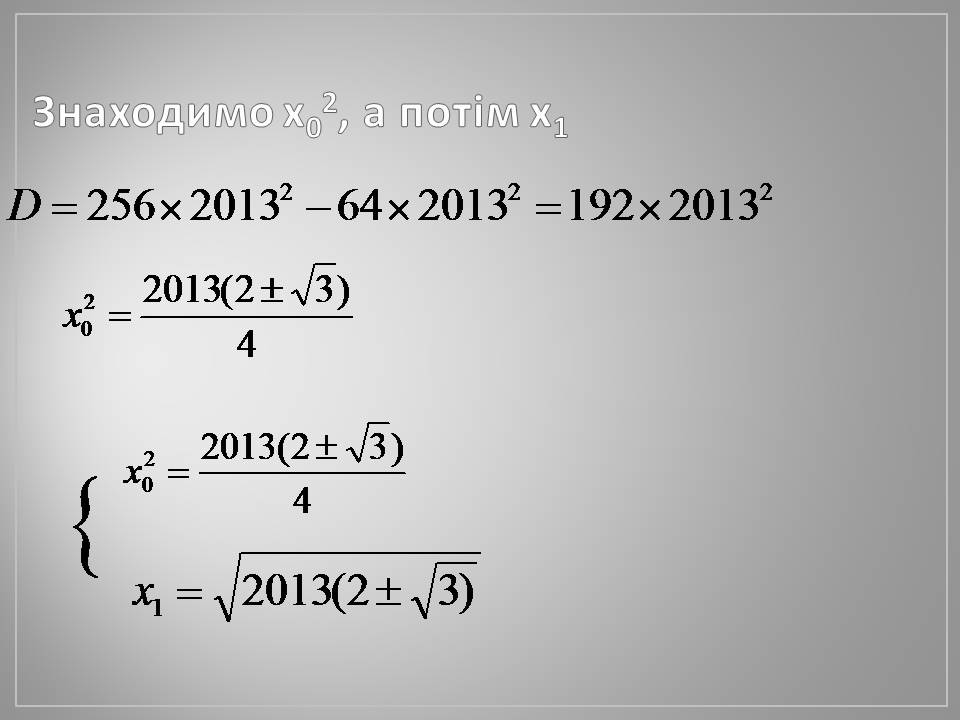
Знаходимо х02, а потім х1
Слайд #16
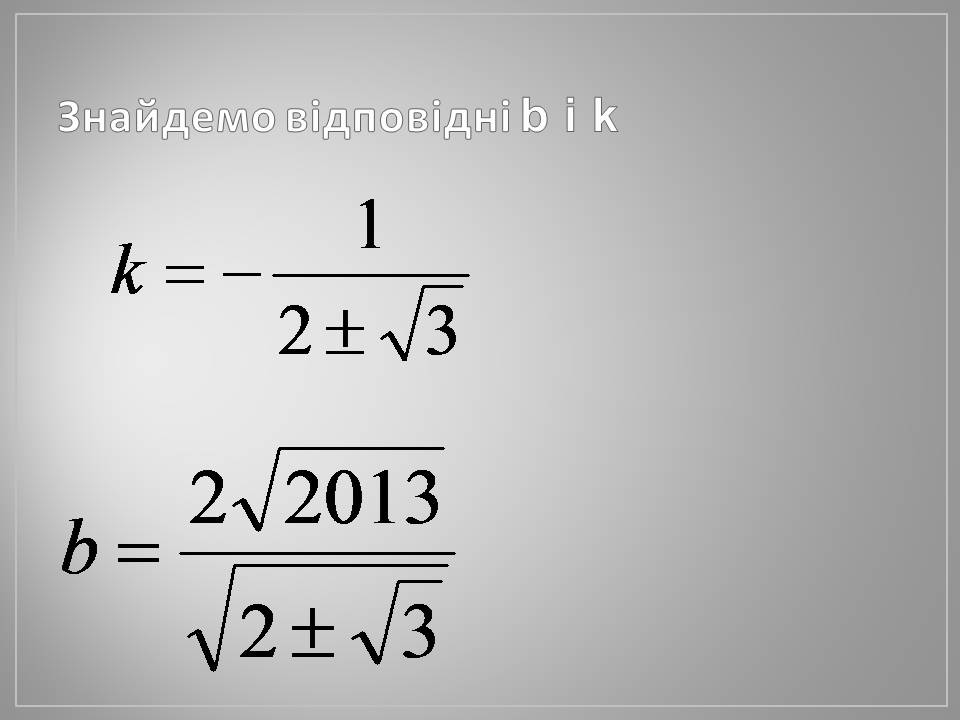
Знайдемо відповідні b i k
Слайд #17
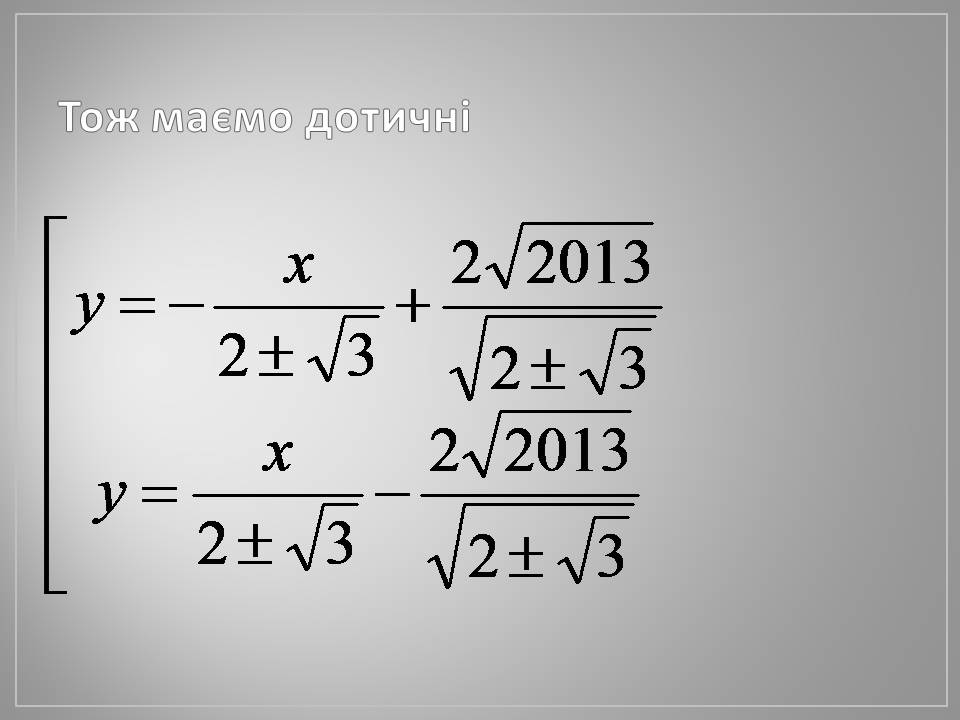
Тож маємо дотичні