Презентація на тему «Блез Паскаль»

Підготувала Алєксєєнко Вероніка 10-Б
Блез Паскаль1623—1662

Французький математик, фізик, релігійний філософ і літератор

Перші роки життя
Клермон-Ферран
Блез Паскаль народився 19 червня 1623 року в місті Клермон-Ферран в сім'ї голови податкового управління Етьєна Паскаля і Антуанетти Бегон. Мав двох сестер: молодша - Жаклін і старша - Жильберта.
Мати померла, коли Блезу було 3 роки.
В 1631 році сім'я переїхала в Париж.
Блез ріс обдарованою дитиною. Його батько Етьєн самостійно займався освітою хлопчика.За його планом стародавні мови Блез повинен був вивчати з 12-ти, а математику з 15-16-річного віку. Батько побоювався, що математика завадить синові вивчати латинську та грецьку мови. Етьєн заборонив йому всякі дослідження в цій області, однак Блез, залишаючись один, почав вугіллям креслити на підлозі різні фігури і вивчати їх. Хлопчик, не знав навіть назв фігур, самостійно довів 32-ю теорему Евкліда про суму кутів трикутника.

Геніальність з дитинства
В 10 років Паскаль створив «Трактат про звуки».
З 14 років Паскаль брав участь у щотижневих семінарах Мерсенна.
В 16 лет він пише математичний трактат «Досвід теорій конічних перетинів».
В 18 років Паскаль починає працювати над створенням обчислювальної машини.

Геніальність з дитинства
В 10 років Паскаль створив «Трактат про звуки».
З 14 років Паскаль брав участь у щотижневих семінарах Мерсенна.
В 16 лет він пише математичний трактат «Досвід теорій конічних перетинів».
В 18 років Паскаль починає працювати над створенням обчислювальної машини.

Трикутник Паскаля — це геометрично, на зразок трикутника, розміщені біноміальні коефіцієнти.
Ряди трикутника Паскаля умовно пронумеровані згори, починаючи з нульового, й числа в нижньому ряді відносно чисел у попередньому ряді завжди розміщені ступінчасто й навскіс. Побудувати цей трикутник просто. Кожне число в кожному ряді одержуємо, додавши два числа, розміщені вгорі (зліва і справа). Якщо зліва або справа немає числа, підставляємо нуль на його місце.
Правило Паскаля стверджує: якщо
k-й біноміальний коефіцієнт в біноміальному ряді для (x + y)n, тоді
для будь-якого додатного цілого n і будь-якого цілого k між 0 і n.
Cnk = Cn-1k + Cn-1k-1
«Трактат про арифметичний трикутник виданий в 1665 році.

Трикутник Паскаля — це геометрично, на зразок трикутника, розміщені біноміальні коефіцієнти.
Ряди трикутника Паскаля умовно пронумеровані згори, починаючи з нульового, й числа в нижньому ряді відносно чисел у попередньому ряді завжди розміщені ступінчасто й навскіс. Побудувати цей трикутник просто. Кожне число в кожному ряді одержуємо, додавши два числа, розміщені вгорі (зліва і справа). Якщо зліва або справа немає числа, підставляємо нуль на його місце.
Правило Паскаля стверджує: якщо
k-й біноміальний коефіцієнт в біноміальному ряді для (x + y)n, тоді
для будь-якого додатного цілого n і будь-якого цілого k між 0 і n.
Cnk = Cn-1k + Cn-1k-1
«Трактат про арифметичний трикутник виданий в 1665 році.

Трикутник Паскаля — це геометрично, на зразок трикутника, розміщені біноміальні коефіцієнти.
Ряди трикутника Паскаля умовно пронумеровані згори, починаючи з нульового, й числа в нижньому ряді відносно чисел у попередньому ряді завжди розміщені ступінчасто й навскіс. Побудувати цей трикутник просто. Кожне число в кожному ряді одержуємо, додавши два числа, розміщені вгорі (зліва і справа). Якщо зліва або справа немає числа, підставляємо нуль на його місце.
Правило Паскаля стверджує: якщо
k-й біноміальний коефіцієнт в біноміальному ряді для (x + y)n, тоді
для будь-якого додатного цілого n і будь-якого цілого k між 0 і n.
Cnk = Cn-1k + Cn-1k-1
«Трактат про арифметичний трикутник виданий в 1665 році.
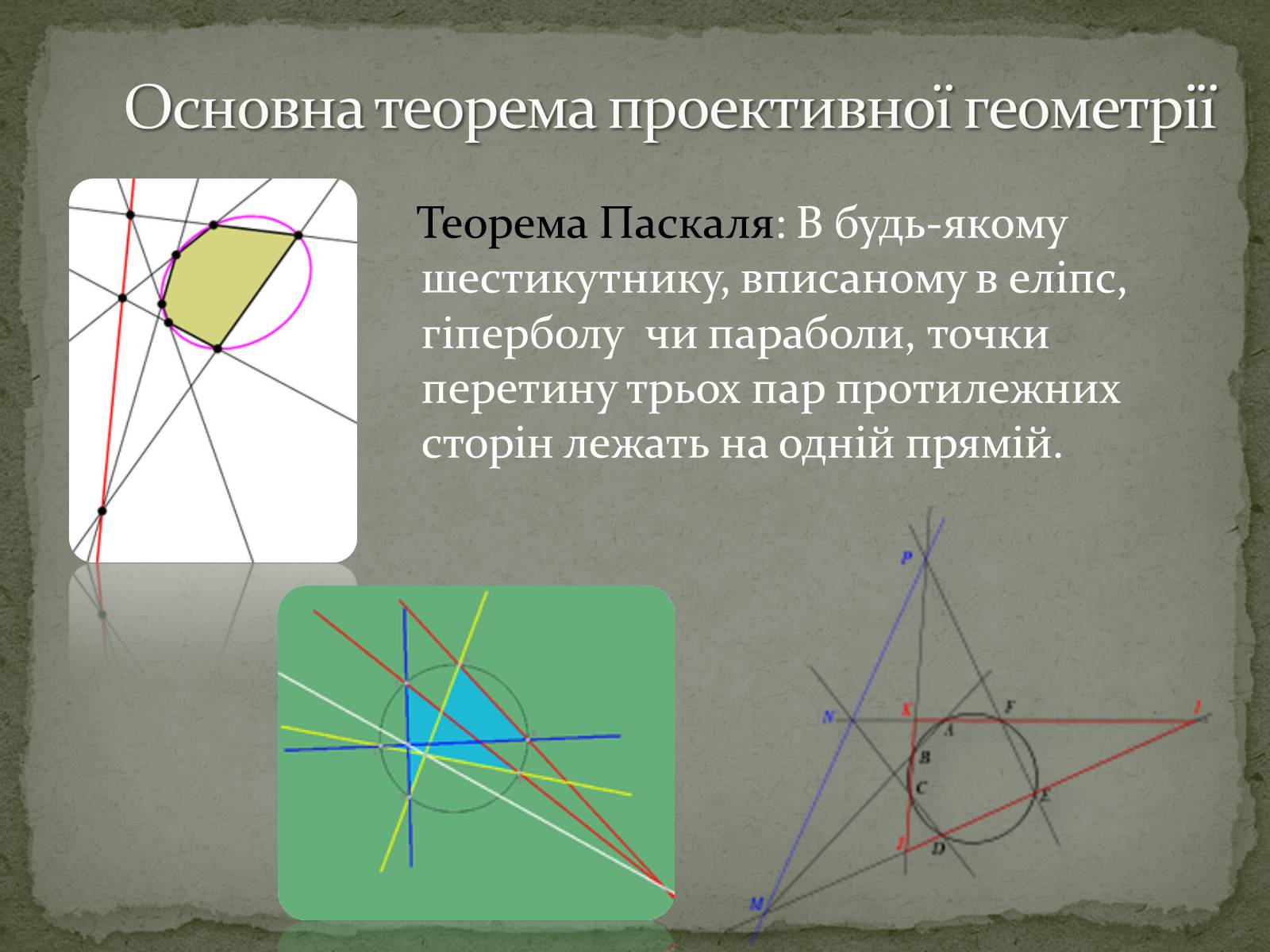
Основна теорема проективної геометрії
Теорема Паскаля: В будь-якому шестикутнику, вписаному в еліпс, гіперболу чи параболи, точки перетину трьох пар протилежних сторін лежать на одній прямій.

Смерть
Причастившись Святих Тайн і провівши останню добу в агонії,
19 серпня 1662, у віці 39 років у Парижі помер Блез Паскаль - велика людина, якій природа дала все, крім фізичного здоров'я.
ПОСМЕРТНА МАСКА Б.ПАСКАЛЯ

На честь Паскаля названі: