Презентація на тему «Закони Кеплера» (варіант 3)

Закони Кеплера
Підготувала
Пехньо Олександра

ЙОГАНН КЕПЛЕР (1571 – 1630)
Видатний німецький астроном і математик, який відкрив закони руху планет навколо Сонця. Кеплер був прихильником учення Коперника і своїми працями сприяв його утвердженню й розвитку.

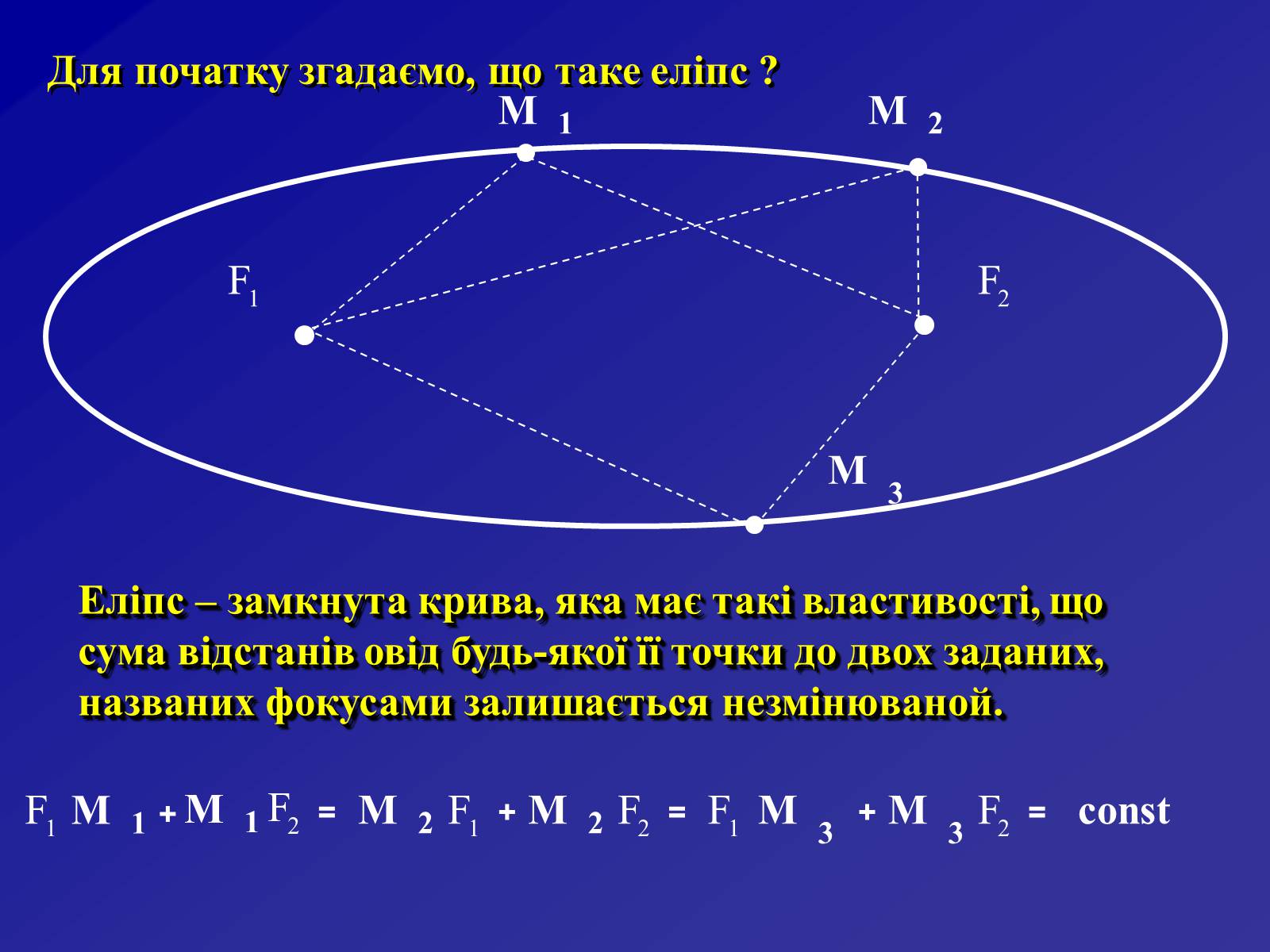
Для початку згадаємо, що таке еліпс ?
Еліпс – замкнута крива, яка має такі властивості, що сума відстанів овід будь-якої її точки до двох заданих, названих фокусами залишається незмінюваной.
F
1
F
2
М
1
М
2
М
3
F
1
М
1
+
М
1
F
2
+
=
F
1
М
2
М
2
F
2
+
=
F
1
М
3
М
3
F
2
=
const

Закони Кеплера
О
F
1
F
2
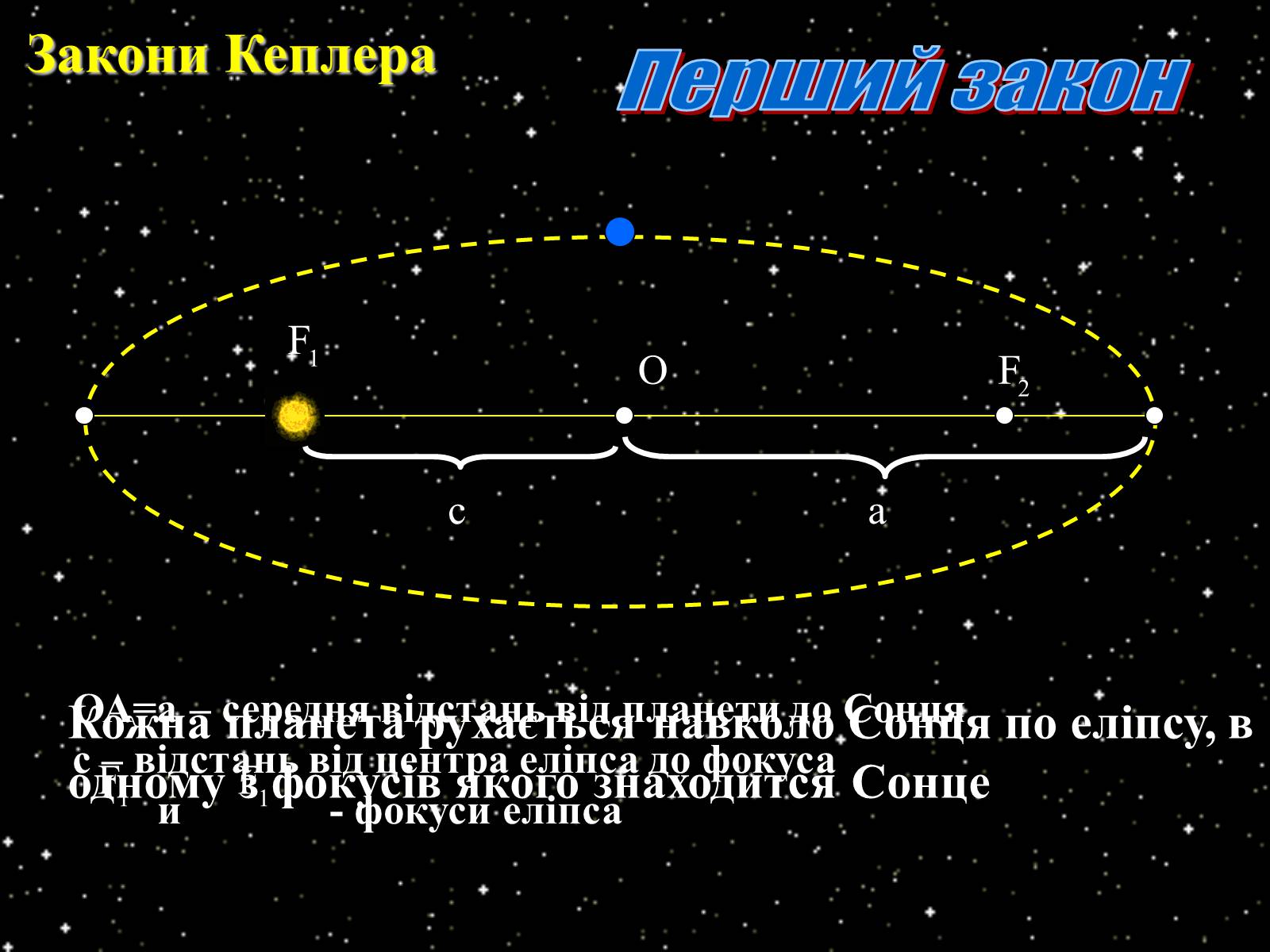
Кожна планета рухається навколо Сонця по еліпсу, в одному з фокусів якого знаходится Сонце
а
с
Перший закон
ОА=а – середня відстань від планети до Сонцяс – відстань від центра еліпса до фокуса и - фокуси еліпса
F
1
F
1

Закони Кеплера
О
F
F
1
2
а
с
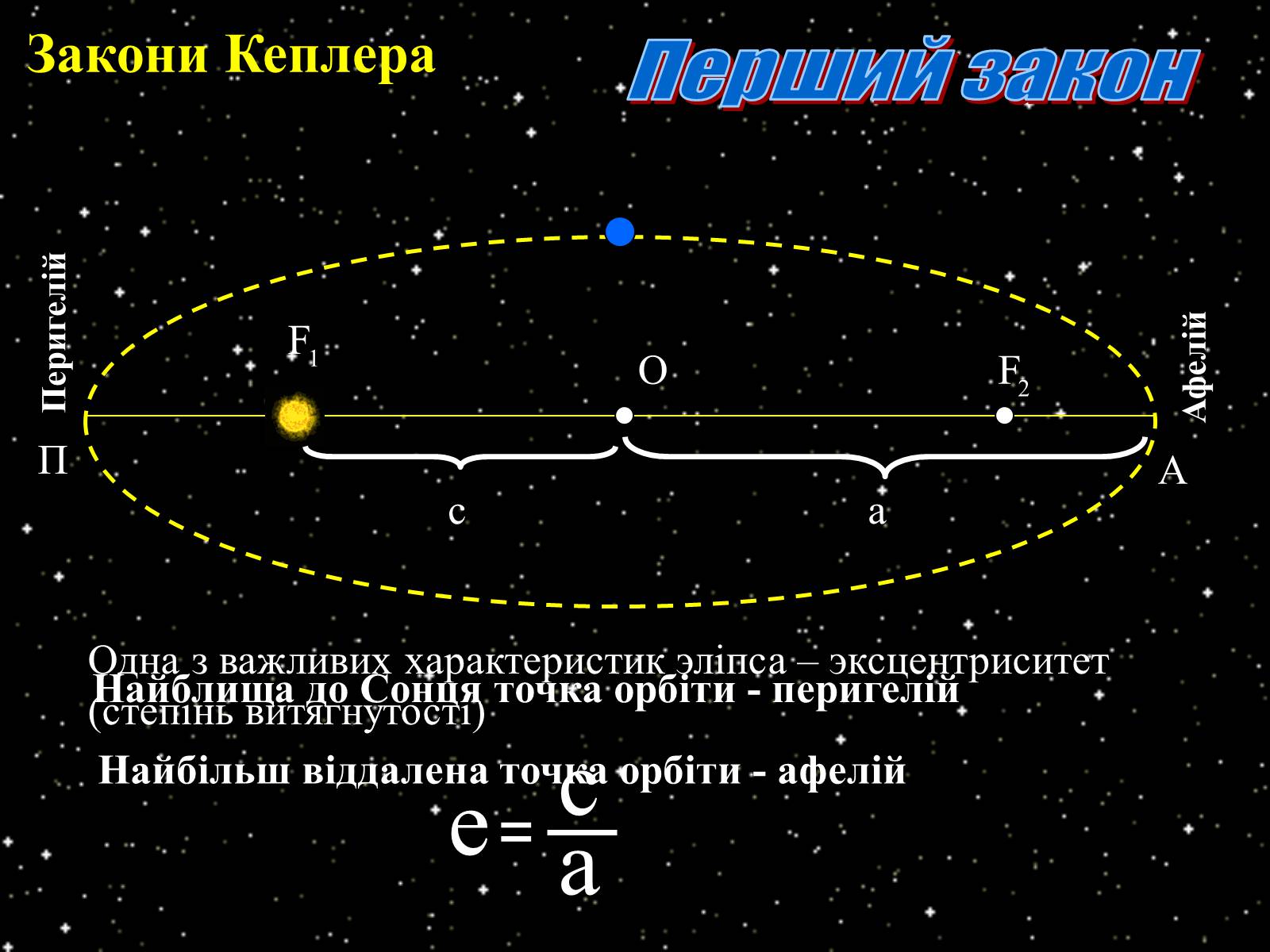
Одна з важливих характеристик эліпса – эксцентриситет (степінь витягнутості)
е
=
с
а
Перший закон
П
Перигелій
А
Афелій
Найблища до Сонця точка орбіти - перигелій
Найбільш віддалена точка орбіти - афелій

Закони Кеплера
F
F
О
1
2
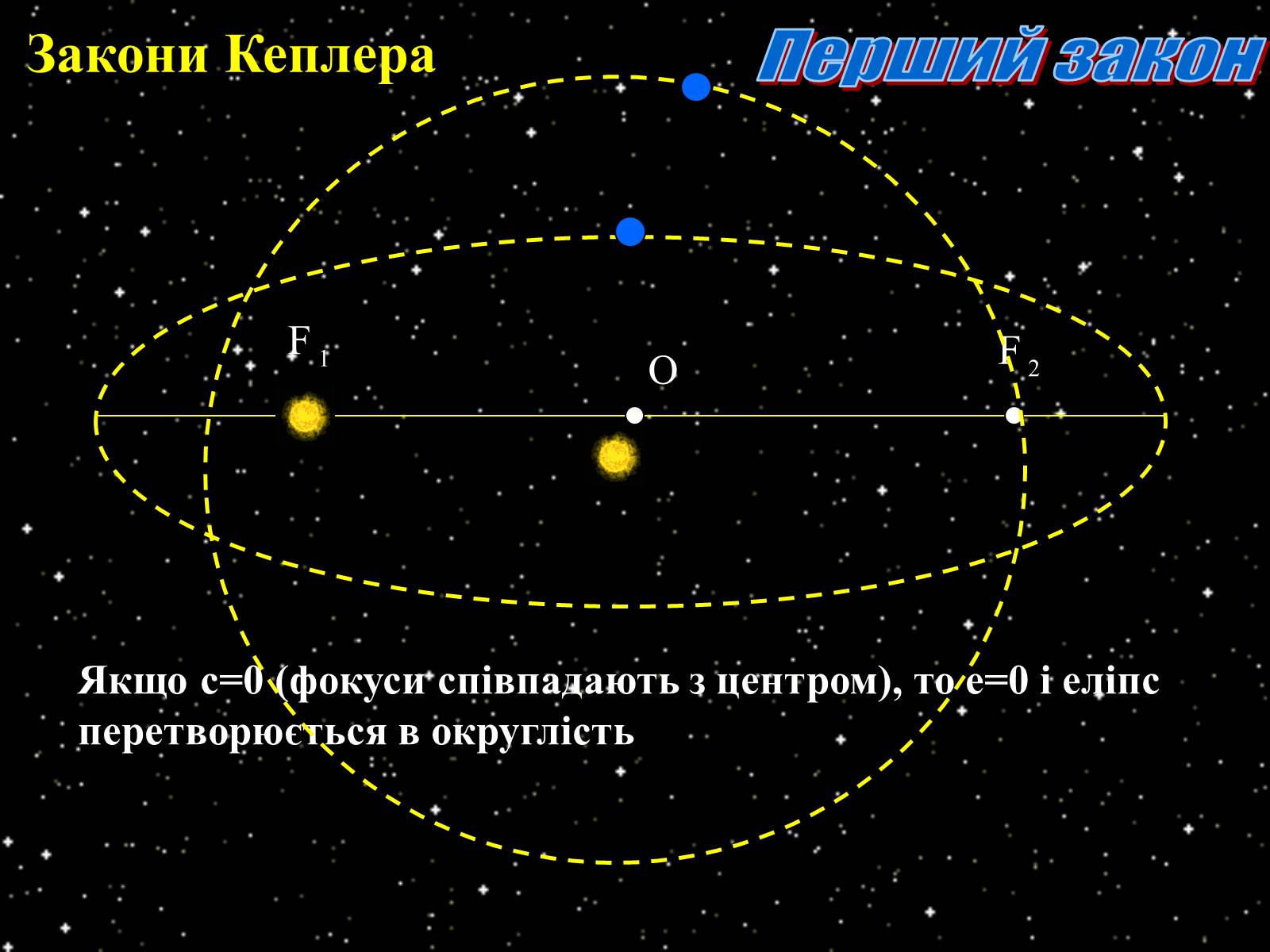
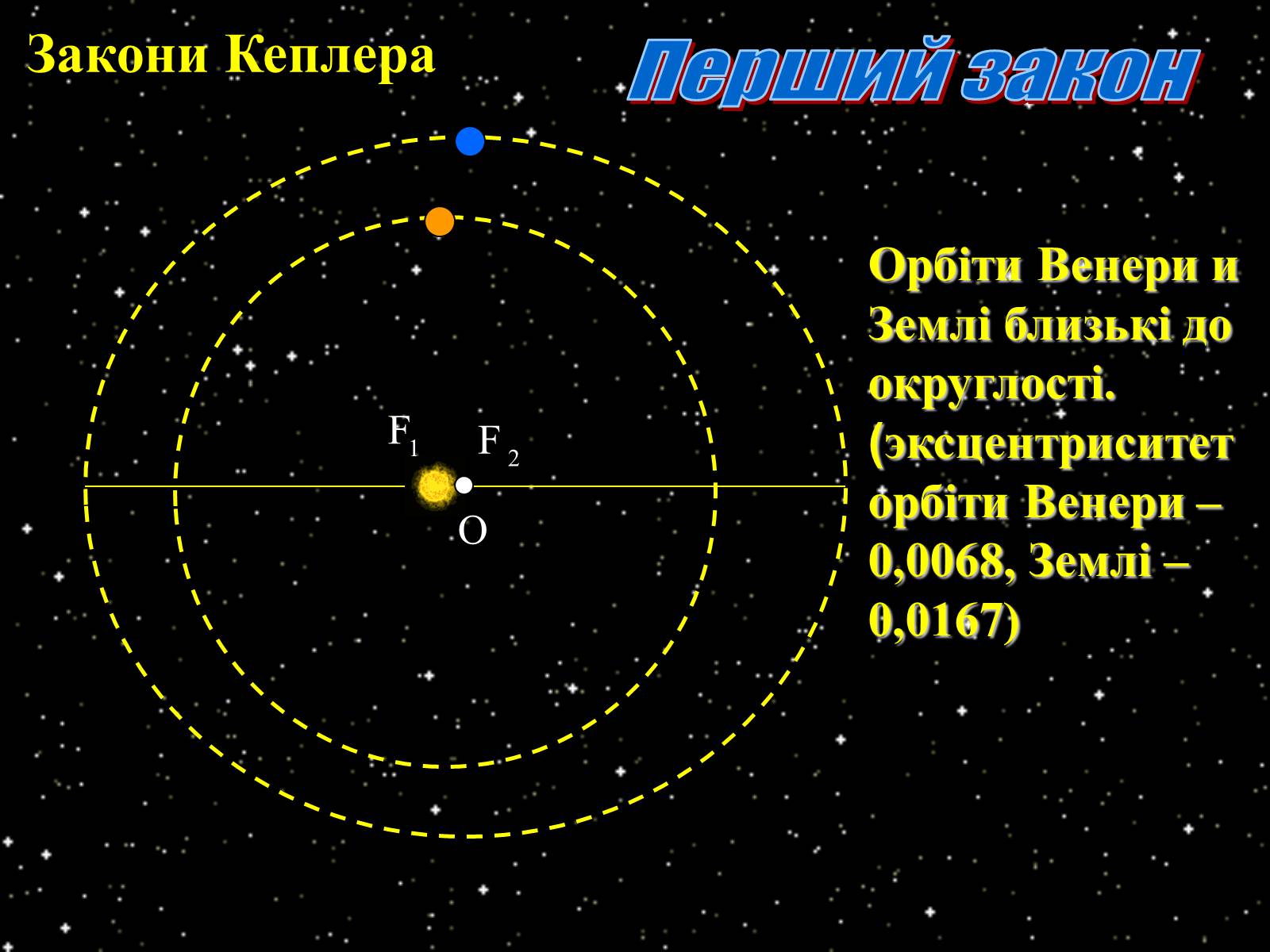
Якщо с=0 (фокуси співпадають з центром), то е=0 і еліпс перетворюється в округлість
Перший закон

Закони Кеплера
О
F
1
F
2
Орбіти Венери и Землі близькі до округлості. (эксцентриситет орбіти Венери – 0,0068, Землі – 0,0167)
Перший закон

Закони Кеплера
Другий закон
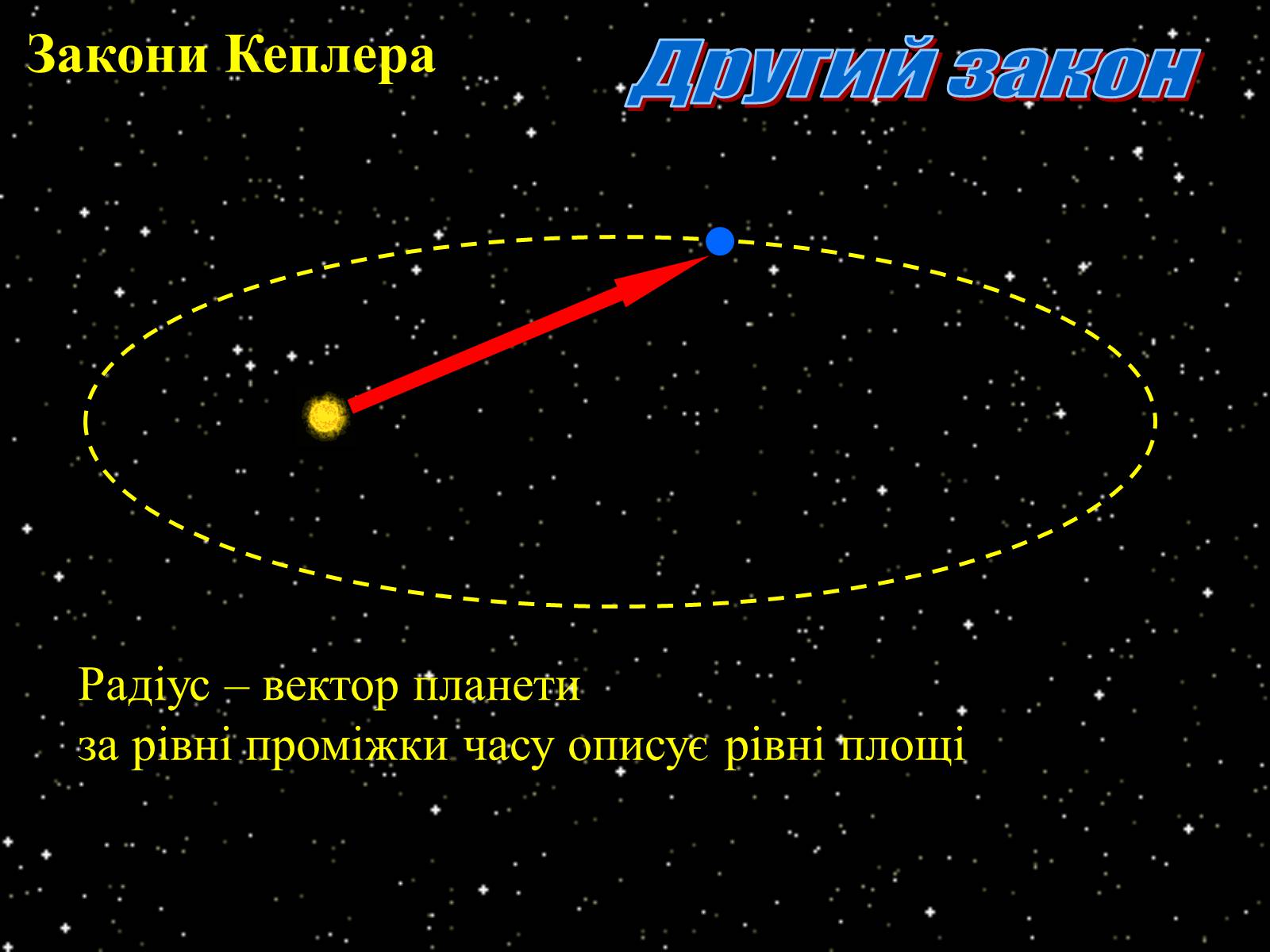
Радіус – вектор планети
за рівні проміжки часу описує рівні площі

Закони Кеплера
Другий закон
П
Перигелій
А
Афелій
S
H
D
C
K
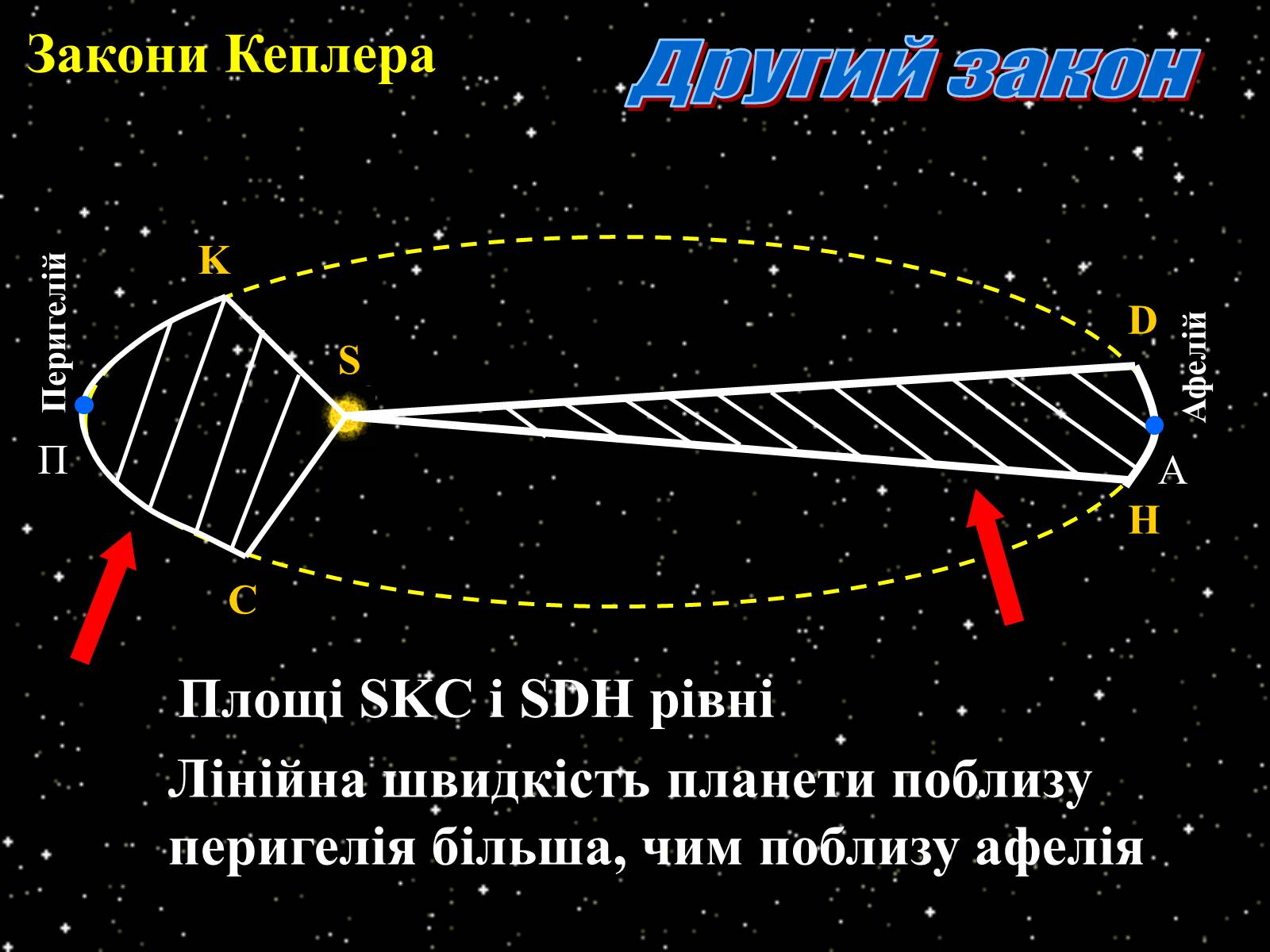
Площі SKC і SDH рівні
Лінійна швидкість планети поблизу перигелія більша, чим поблизу афелія

Закони Кеплера
О
F
1
F
2
Третій закон
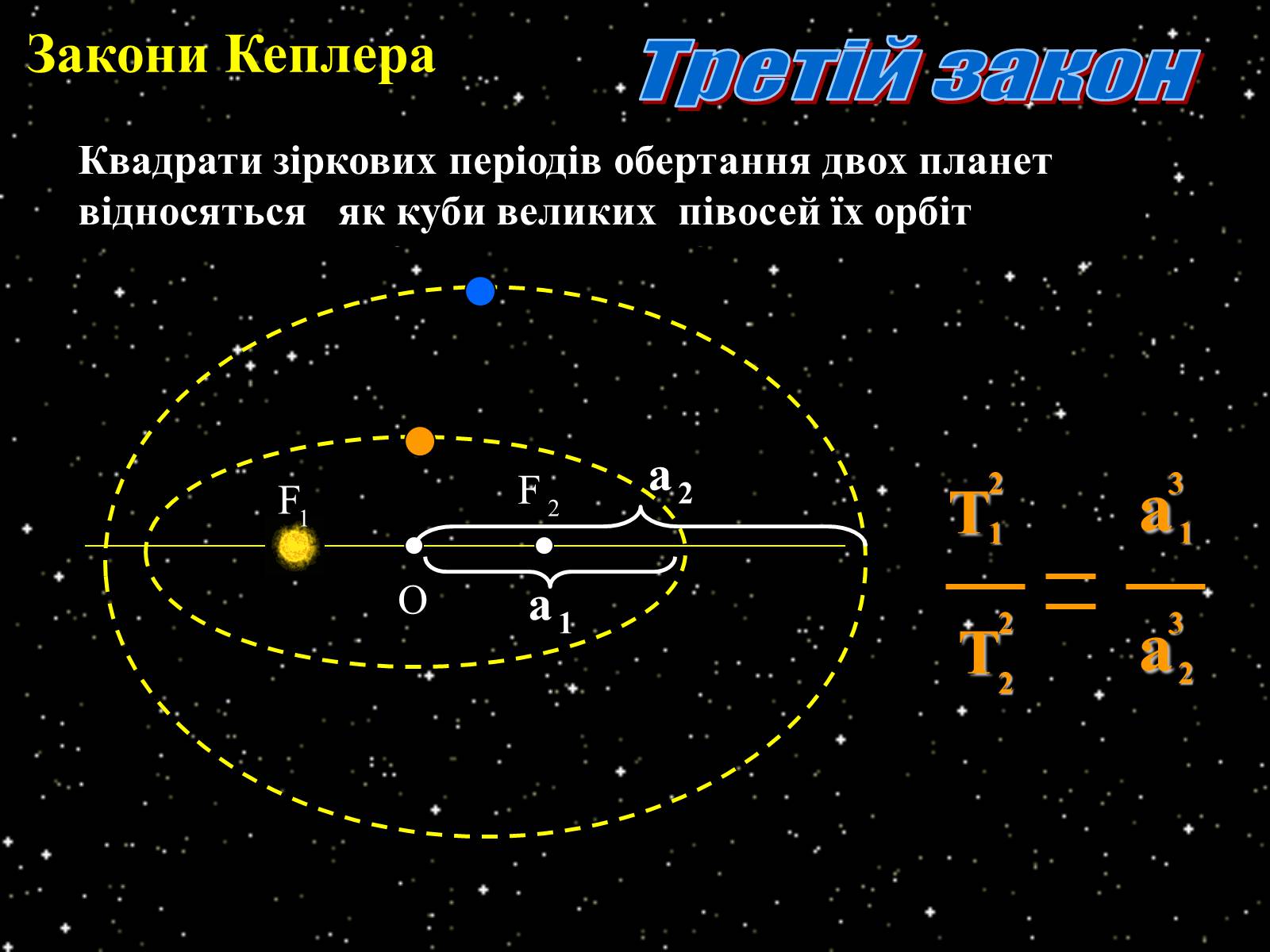
Квадрати зіркових періодів обертання двох планет відносяться як куби великих півосей їх орбіт
Т
2
2
Т
1
2
а
2
3
а
1
3
а
1
а
2

ВИДИМІ
РУХИ
ПЛАНЕТ

Вступ
Ще здавна серед "нерухомих зір" мешканці Землі помітили "блукаючі зорі", які грецькою мовою називаються планетами. Тоді були відомі 7 "блукаючих зір": зореподібні - Меркурій, Венера, Марс, Юпітер і Сатурн, а також дископодібні - Сонце та Місяць. Згодом, коли з'ясувалось, що Сонце є найближчою до нас зорею, а Місяць є супутником нашої планети Земля, назва "планети" закріпилась лише за тими космічними об'єктами, які обертаються навколо Сонця. Ще пізніше, крім згаданих планет, були відкриті планети Уран, Нептун і Плутон, декілька десятків супутників планет, а також декілька тисяч так званих малих планет (астероїдів).

Вступ
Ще здавна серед "нерухомих зір" мешканці Землі помітили "блукаючі зорі", які грецькою мовою називаються планетами. Тоді були відомі 7 "блукаючих зір": зореподібні - Меркурій, Венера, Марс, Юпітер і Сатурн, а також дископодібні - Сонце та Місяць. Згодом, коли з'ясувалось, що Сонце є найближчою до нас зорею, а Місяць є супутником нашої планети Земля, назва "планети" закріпилась лише за тими космічними об'єктами, які обертаються навколо Сонця. Ще пізніше, крім згаданих планет, були відкриті планети Уран, Нептун і Плутон, декілька десятків супутників планет, а також декілька тисяч так званих малих планет (астероїдів).

Вступ
Ще здавна серед "нерухомих зір" мешканці Землі помітили "блукаючі зорі", які грецькою мовою називаються планетами. Тоді були відомі 7 "блукаючих зір": зореподібні - Меркурій, Венера, Марс, Юпітер і Сатурн, а також дископодібні - Сонце та Місяць. Згодом, коли з'ясувалось, що Сонце є найближчою до нас зорею, а Місяць є супутником нашої планети Земля, назва "планети" закріпилась лише за тими космічними об'єктами, які обертаються навколо Сонця. Ще пізніше, крім згаданих планет, були відкриті планети Уран, Нептун і Плутон, декілька десятків супутників планет, а також декілька тисяч так званих малих планет (астероїдів).

Найпростіше помітити "блукання" Місяця серед зір, бо він швидко рухається із заходу на схід і за 27.3 доби "пробігає" всю небесну сферу, тобто здійснює повний оберт. Якщо в якусь ніч примітити його положення по відношенню до найближчих зір, то вже наступної ночі Місяць знаходитиметься в оточенні інших зір, бо за добу переміститься по небу на 13.2".

Найпростіше помітити "блукання" Місяця серед зір, бо він швидко рухається із заходу на схід і за 27.3 доби "пробігає" всю небесну сферу, тобто здійснює повний оберт. Якщо в якусь ніч примітити його положення по відношенню до найближчих зір, то вже наступної ночі Місяць знаходитиметься в оточенні інших зір, бо за добу переміститься по небу на 13.2".

Переміщення Сонця серед зір не можна спостерігати безпосередньо, бо зорі вдень невидимі. Проте, якщо замітити якусь зорю поблизу горизонту в західній частині неба невдовзі після заходу Сонця і спробувати її відшукати через декілька днів в той же час, то можна помітити, що вона знизилась і ніби наблизилась до Сонця. Ще через декілька днів зоря зникне за горизонтом, а її місце займе інша зоря, яка раніше знаходилась на схід від першої. Надалі і ця зоря теж наближатиметься до Сонця. Саме за такими спостереженнями можна зробити висновок про зміну положення Сонця серед зір.

В давні часи спостереження за положеннями зір та планет проводились регулярно, що надало можливість визначити видимий шлях Сонця по небу. Виявилось, що Сонце, як і Місяць, рухається із заходу на схід і за 365.25 доби його видимий шлях набуде вигляду кола на небесній сфері, тобто через цей інтервал часу воно повертається до тих же самих зір. Річний шлях Сонця серед зір назвали екліптикою, яка за уявленнями древніх не змінює свого положення по відношенню до зір. За добу Сонце зміщується вздовж екліптики на схід приблизно на 1є.

Більш складним виявився рух зореподібних планет, які завжди розташовані поблизу екліптики. Нижні планети Меркурій і Венера ніби коливаються відносно Сонця. Спочатку планета рухається серед зір швидше за Сонце і обганяє його. Потім на певній кутовій відстані на схід від Сонця планета сповільнює свій рух, а Сонце наздоганяє та випереджає планету. Через деякий час, досягнувши максимального кутового віддалення на захід від Сонця, планета знову починає рухатися швидше і наздоганяє його. Надалі увесь цикл повторюється.

Найбільше віддалення від Сонця сягає 40є для Венери і в середньому 23° (від 18 до 28°) для Меркурія. Ось тому Меркурій і Венера видимі тільки або вранці на сході, незадовго до сходу Сонця, або увечері на заході, після заходу Сонця. Для верхніх планет - Марса, Юпітера, Сатурна, Урана і Нептуна - характерні "петлі" на небі. В основному ці планети переміщуються серед зір із заходу на схід. Проте в певні періоди кожна з них сповільнює свій рух, зупиняється серед зір, а згодом починає рухатись у зворотному напрямку, тобто зі сходу на захід. Ще через деякий час планета знову зупиняється і починає рухатись у звичайному для неї напрямку. Таким чином, спостерігач має можливість зафіксувати в рухові планет "петлі". Марс здійснює їх через кожні 780, Юпітер - 399, а Сатурн - 378 діб.

Перші кроки завжди важкі
Перші спроби пояснити видимі переміщення планет на небі, а заодно створити теорії руху з метою передбачення їхніх положень в будь-який наступний чи минулий момент належать стародавнім грекам і вавілонянам. Зокрема відомо, що одна з перших астрономічних доктрин для пояснення руху планет була запропонована Евдоксом Кнідським (біля 410-350 р. до н. е) і базувалась па системі концентричних сфер, в центрі яких знаходиться Земля. Згідно Евдоксу видимий рух кожної планети можна відтворити за допомогою чотирьох сфер, кожна з яких обертається рівномірно навколо своєї осі.

Осі всіх сфер перетинаються в одній точці, але мають різні нахили. За цією концепцією дві сфери обертаються із заходу на схід, а дві інші в протилежному напрямку, до того ж періоди обертання сфер приймаються різними. Кожна із сфер, незалежно від її власного обертання, "сприймає" рух інших зовнішніх по відношенню до неї сфер. На екваторі внутрішної четвертої сфери знаходиться точка, яка зображає певну планету. Складний рух точки з урахуванням напрямку обертання всіх чотирьох сфер, періодів їхнього обертання і нахилу осей відтворює видимий рух планет з тими особливостями, про які згадувалось вище. Подальше вдосконалення системи Евдокса запропонував Каліпп, який збільшив число сфер до п'яти для Сонця, Місяця, Меркурія. Венери і Марса. Загалом, в теорії Каліппа нараховувалось 33 сфери для всіх планет.

Згодом Аристотель ускладнив ще більше моделі Евдокса і Каліппа. Нагадаємо ще, що з праць Архімеда відомо про запропоновану ще в III ст. до н.е. Арістархом Самосським завершену модель геліоцентричної системи світу, в якій Земля разом з Олімпом і помешканням богів оберталась навколо своєї осі. На жаль, це вчення не було сприйняте позитивно, а перемогло уявлення про геоцентричну будову світу, яким користувались аж до XVI ст.

До нас дійшли й інші свідчення про погляди на будову світу та про пояснення особливостей руху планет. Проте, на нашу думку, на цьому більш детально зупинятись не варто. Зауважимо лише, що матеріали цих вчених древності не збереглись у письмовому вигляді. Ми маємо лише свідчення так званих коментаторів їхніх вчень, тому неможливо проаналізувати математичні основи згаданих теорій, результати і точність обчислень для передбачення руху планет.

Сучасні теорії руху небесних тіл
Серед найбільш досконалих аналітичних теорій руху необхідно згадати планетні теорії Левер'є, створені в 50-60-х pp. минулого століття. Вони мають вигляд таблиць, в яких положення Сонця і семи великих планет (крім Плутона) відносно Землі подані в залежності від часу. Згодом з'ясувалося, що розбіжність положень, обчислених за теоріями Левер'є і нових спостережень почала збільшуватись, зокрема це найбільше стосувалось Юпітера і Сатурна. В зв'язку з цим американський астроном Хілл в 1895 р. побудував також аналітичні теорії руху Юпітера і Сатурна, проте і вони не усунули розбіжності теорій і спостережень. Тому Гайо в 1913 р. здійснив уточнення теорії і довів розбіжність до розмірів похибок спостережень.

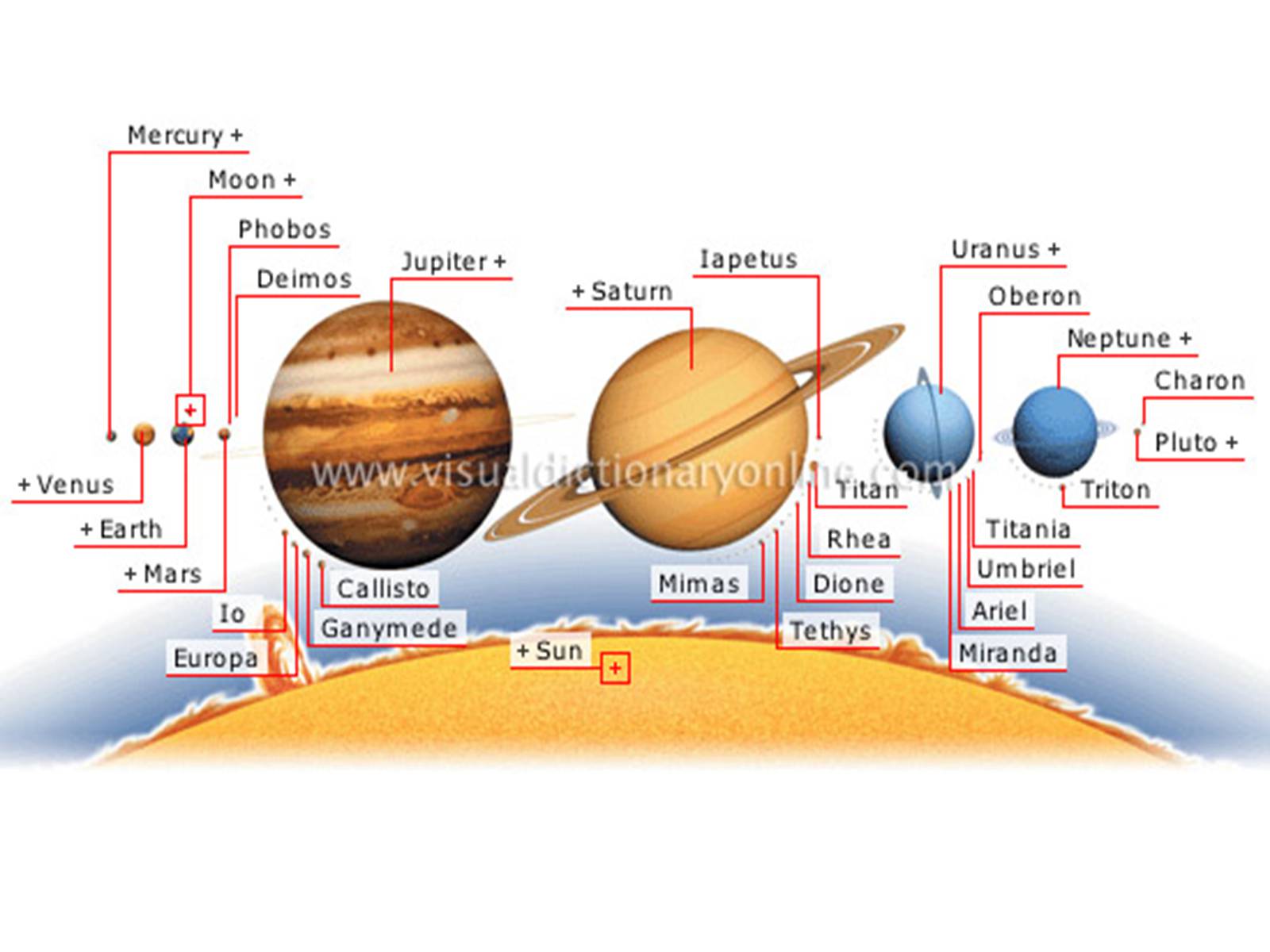
Сучасні теорії руху небесних тіл
Серед найбільш досконалих аналітичних теорій руху необхідно згадати планетні теорії Левер'є, створені в 50-60-х pp. минулого століття. Вони мають вигляд таблиць, в яких положення Сонця і семи великих планет (крім Плутона) відносно Землі подані в залежності від часу. Згодом з'ясувалося, що розбіжність положень, обчислених за теоріями Левер'є і нових спостережень почала збільшуватись, зокрема це найбільше стосувалось Юпітера і Сатурна. В зв'язку з цим американський астроном Хілл в 1895 р. побудував також аналітичні теорії руху Юпітера і Сатурна, проте і вони не усунули розбіжності теорій і спостережень. Тому Гайо в 1913 р. здійснив уточнення теорії і довів розбіжність до розмірів похибок спостережень.

Поліпшені теорії Левер'є були основними в астрономії до початку XX ст., а для зовнішніх планет використовувались ще тривалий час в першій половині XX ст. В 1895-1898 pp. Нюкомом були опубліковані нові аналітичні теорії руху Меркурія, Венери, Землі, Марса, Урана і Нептуна теж у вигляді таблиць. Вони базувались на положеннях, спостережених на всіх обсерваторіях світу з 1750 р. по 1892 p.: 40000 положень для Сонця, 5400 положень і 4 проходження по диску Сонця для Меркурія, 12000 положень і 2 проходження по диску Сонця для Венери, 4000 положень для Марса. Проте і тут не обійшлось без несподіванок. Спостереження Марса в опозицію 1902-1903 pp. розбігались з теорією на 3", а в опозицію 1905 р. - вже на 6". Як згодом з'ясував Росе, причиною розбіжності теорії і спостережень було помилкове на 0.7" значення ексцентриситету, прийняте Нюкомом для обчислень. Тому Росе ввів поправки до Нюкомової теорії для Марса.

Пізніше ще вносились деякі уточнення в теорії Нюкома, з якими вони і використовувались для внутрішніх планет аж до 80-х років XX ст. Що стосується теорій руху зовнішніх планет, то вони були менш точними. Ось тому вже в 50-х роках XX ст. теорії Нюкома для Юпітера, Сатурна, Урана, Нептуна були замінені чисельними теоріями, побудованими Еккертом, Брауером і Клеменсом шляхом чисельного інтегрування диференціальних рівнянь руху. У 80-х роках астрономи перейшли на використання чисельної теорії руху планет DE200, а в 1997 р. Міжнародним астрономічним союзом рекомендовані ще більш досконалі чисельні теорії руху планет DE403.

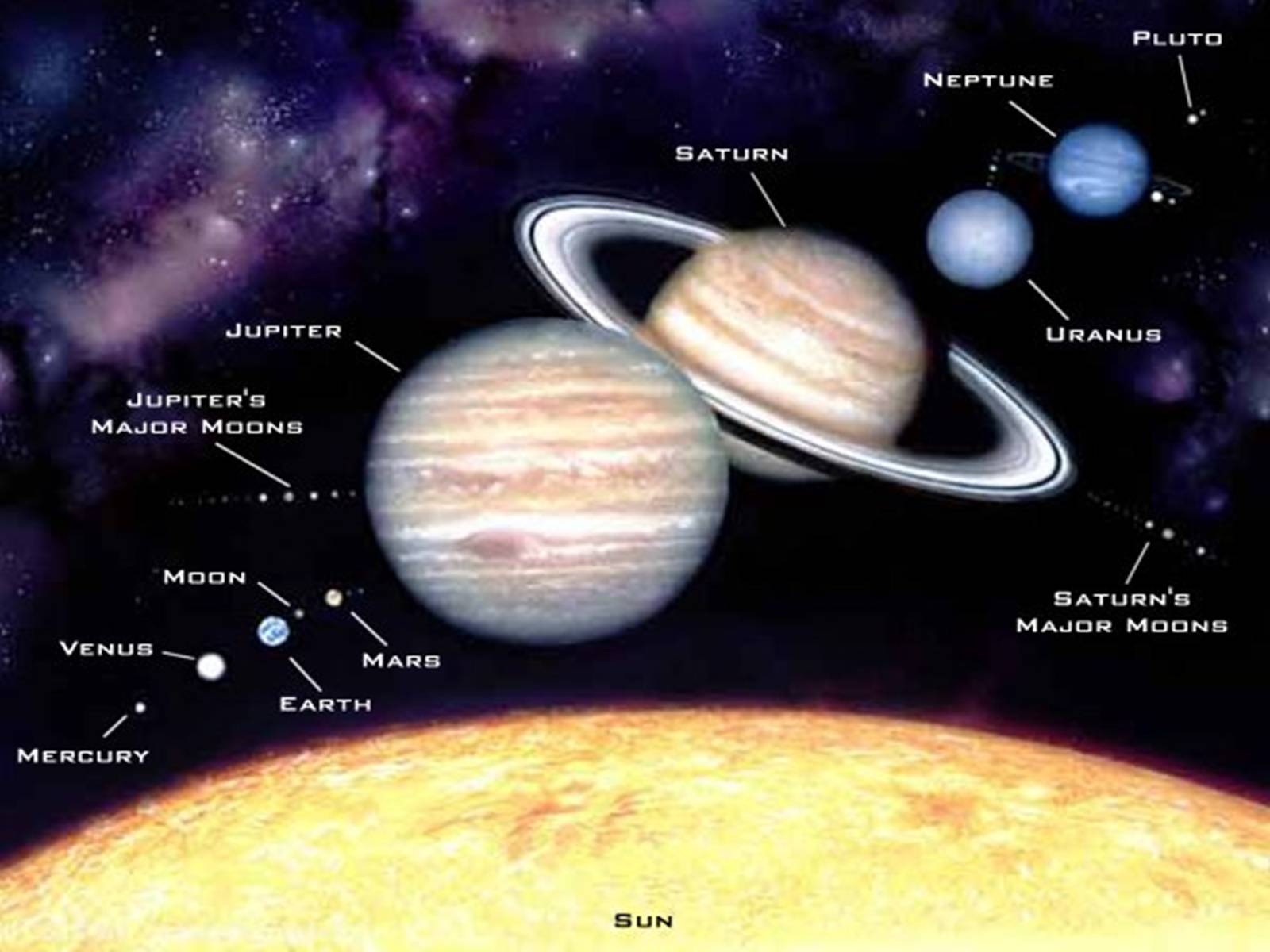
Пізніше ще вносились деякі уточнення в теорії Нюкома, з якими вони і використовувались для внутрішніх планет аж до 80-х років XX ст. Що стосується теорій руху зовнішніх планет, то вони були менш точними. Ось тому вже в 50-х роках XX ст. теорії Нюкома для Юпітера, Сатурна, Урана, Нептуна були замінені чисельними теоріями, побудованими Еккертом, Брауером і Клеменсом шляхом чисельного інтегрування диференціальних рівнянь руху. У 80-х роках астрономи перейшли на використання чисельної теорії руху планет DE200, а в 1997 р. Міжнародним астрономічним союзом рекомендовані ще більш досконалі чисельні теорії руху планет DE403.

Першу наближену теорію руху Місяця створив Ейлер ще в 1722 р. Через 100 років Хілл розвинув ідеї Ейлера, і були закладені найбільш точні, теоретичні основи для обчислення положень Місяця. Найдосконаліша аналітична теорія руху Місяця створена Брауном і опублікована в 1919 р. Це був результат майже 30-річної праці Брауна, який, по суті, продовжив та розвинув надбання Хілла. Відтоді теорія руху Місяця неодноразово уточнювалась. Спочатку в 1960 р. теорія Брауна була поліпшена за рахунок введення в середню довготу Місяця емпіричної нерівності 8.72" - 26.74"Г - 11.227", пояснення якої до цього часу було проблематичним. Надалі після 1971 р. була виправлена помилка в 182 членові місячної теорії Брауна і був здійснений перехід на систему астрономічних сталих МАС 1964 р.

Першу наближену теорію руху Місяця створив Ейлер ще в 1722 р. Через 100 років Хілл розвинув ідеї Ейлера, і були закладені найбільш точні, теоретичні основи для обчислення положень Місяця. Найдосконаліша аналітична теорія руху Місяця створена Брауном і опублікована в 1919 р. Це був результат майже 30-річної праці Брауна, який, по суті, продовжив та розвинув надбання Хілла. Відтоді теорія руху Місяця неодноразово уточнювалась. Спочатку в 1960 р. теорія Брауна була поліпшена за рахунок введення в середню довготу Місяця емпіричної нерівності 8.72" - 26.74"Г - 11.227", пояснення якої до цього часу було проблематичним. Надалі після 1971 р. була виправлена помилка в 182 членові місячної теорії Брауна і був здійснений перехід на систему астрономічних сталих МАС 1964 р.

Нарешті, було здійснене ще одне поліпшення теорії, яке зводиться до заміни співвідношень Брауна для збурень від Сонця співвідношеннями Еккерта. Загалом, теорія руху Місяця за Брауном подається у вигляді тригонометричних рядів із складним аргументом, який залежить від часу, вікових і періодичних збурень. Ряди налічують понад 1650 членів. Щоб обчислити, наприклад, довготу Місяця з точністю до 0.1", необхідно скласти 655 членів. Проте необхідно зауважити, що точність 0 1" є лише точністю обчислень, а справжня розбіжність обчислених і спостережених положень Місяця в багато разів більша.

В останні десятиріччя замість теорії Брауна набули поширення чисельні теорії руху Місяця DL200 і DL403, кожна з яких вводилась одночасно з DE200 і DE403. Як же оцінюється сучасний стан теорій руху планет і Місяця? Найбільш оптимальним критерієм досконалості теорій руху планет, їхніх супутників, астероїдів і комет вважається узгодженість обчислених і спостережених положень на коротких (десятки і сотні років) та історично тривалих (тисячі і сотні тисяч років) інтервалах часу.

Перш за все, ця узгодженість залежить від точності врахування періодичних і вікових збурень. Періодичні збурення характеризують відхилення від руху по еліптичних орбітах в одну або іншу сторону. Для планет періодичні збурення порівняно невеликі. Зокрема, найбільші видимі відхилення на небі від еліптичного руху становлять для Меркурія біля 15", Венери - 30", Землі - Г, Марса - 2', Урана - З', Нептуна - 1.5', а для масивних планет Юпітера і Сатурна відхилення сягають 28' і 48'.

Перш за все, ця узгодженість залежить від точності врахування періодичних і вікових збурень. Періодичні збурення характеризують відхилення від руху по еліптичних орбітах в одну або іншу сторону. Для планет періодичні збурення порівняно невеликі. Зокрема, найбільші видимі відхилення на небі від еліптичного руху становлять для Меркурія біля 15", Венери - 30", Землі - Г, Марса - 2', Урана - З', Нептуна - 1.5', а для масивних планет Юпітера і Сатурна відхилення сягають 28' і 48'.

При порівнянні сучасних аналітичних і чисельних теорій руху планет з даними спостережень з 1800 р. по теперішній час мають місце розходження періодичного характеру не більше декількох секунд. Це свідчить про те, що наявні теорії руху придатні для користування на інтервалі 100-200 років. За цей час елементи орбіт будуть змінюватись у відповідності з тими формулами, які покладені в основу теорій. Чи будуть елементи змінюватись надалі так - невідомо.

Вікові збурення регулярно збільшують відхилення від незбуреного руху. З їхнього аналізу можна впевнитись в зміні деяких елементів орбіт планет до таких величин, які є нереальними. Наприклад, для Венери розрахований ексцентриситет орбіти за теорією Левер'є через 20 тисяч років набуде від'ємного значення. Проте він не може бути меншим нуля.

На коротких інтервалах часу теж відомі факти неузгодженості аналітичних теорій руху планет і спостережень до 1". Зокрема, час від часу в публікаціях з'являються повідомлення про додаткові вікові зміни довгот перигеліїв і вузлів орбіт деяких планет, не знайдено пояснення так званого непрецесійного руху рівнодення біля 1" в століття та інше. Це невеликі відхилення, але вони є свідченням про необхідність уточнення теорій руху тіл Сонячної системи.

Найбільші ускладнення виникають при створенні теорій руху супутників планет, зокрема Місяця. Це пояснюється необхідністю досконалого знання гравітаційної фігури та внутрішньої будови планет, які мало вивчені. Для Місяця проблема створення теорії руху ускладнюється ще й близьким розташуванням його відносно Сонця, яке є масивним тілом і суттєво збурює рух в орбіті. Саме тому, ще в 60-70-х роках XX ст. три рази уточнювалась остання аналітична теорія руху Місяця, створена Брауном. Зокрема, лише в 60-х роках знайшла пояснення і була виключена з розряду емпіричних нерівність понад 9". Для низки супутників інших планет теорії руху є ще досить наближеними.

Найбільші ускладнення виникають при створенні теорій руху супутників планет, зокрема Місяця. Це пояснюється необхідністю досконалого знання гравітаційної фігури та внутрішньої будови планет, які мало вивчені. Для Місяця проблема створення теорії руху ускладнюється ще й близьким розташуванням його відносно Сонця, яке є масивним тілом і суттєво збурює рух в орбіті. Саме тому, ще в 60-70-х роках XX ст. три рази уточнювалась остання аналітична теорія руху Місяця, створена Брауном. Зокрема, лише в 60-х роках знайшла пояснення і була виключена з розряду емпіричних нерівність понад 9". Для низки супутників інших планет теорії руху є ще досить наближеними.

Найбільші ускладнення виникають при створенні теорій руху супутників планет, зокрема Місяця. Це пояснюється необхідністю досконалого знання гравітаційної фігури та внутрішньої будови планет, які мало вивчені. Для Місяця проблема створення теорії руху ускладнюється ще й близьким розташуванням його відносно Сонця, яке є масивним тілом і суттєво збурює рух в орбіті. Саме тому, ще в 60-70-х роках XX ст. три рази уточнювалась остання аналітична теорія руху Місяця, створена Брауном. Зокрема, лише в 60-х роках знайшла пояснення і була виключена з розряду емпіричних нерівність понад 9". Для низки супутників інших планет теорії руху є ще досить наближеними.

Найбільші ускладнення виникають при створенні теорій руху супутників планет, зокрема Місяця. Це пояснюється необхідністю досконалого знання гравітаційної фігури та внутрішньої будови планет, які мало вивчені. Для Місяця проблема створення теорії руху ускладнюється ще й близьким розташуванням його відносно Сонця, яке є масивним тілом і суттєво збурює рух в орбіті. Саме тому, ще в 60-70-х роках XX ст. три рази уточнювалась остання аналітична теорія руху Місяця, створена Брауном. Зокрема, лише в 60-х роках знайшла пояснення і була виключена з розряду емпіричних нерівність понад 9". Для низки супутників інших планет теорії руху є ще досить наближеними.

Найбільші ускладнення виникають при створенні теорій руху супутників планет, зокрема Місяця. Це пояснюється необхідністю досконалого знання гравітаційної фігури та внутрішньої будови планет, які мало вивчені. Для Місяця проблема створення теорії руху ускладнюється ще й близьким розташуванням його відносно Сонця, яке є масивним тілом і суттєво збурює рух в орбіті. Саме тому, ще в 60-70-х роках XX ст. три рази уточнювалась остання аналітична теорія руху Місяця, створена Брауном. Зокрема, лише в 60-х роках знайшла пояснення і була виключена з розряду емпіричних нерівність понад 9". Для низки супутників інших планет теорії руху є ще досить наближеними.

Найбільші ускладнення виникають при створенні теорій руху супутників планет, зокрема Місяця. Це пояснюється необхідністю досконалого знання гравітаційної фігури та внутрішньої будови планет, які мало вивчені. Для Місяця проблема створення теорії руху ускладнюється ще й близьким розташуванням його відносно Сонця, яке є масивним тілом і суттєво збурює рух в орбіті. Саме тому, ще в 60-70-х роках XX ст. три рази уточнювалась остання аналітична теорія руху Місяця, створена Брауном. Зокрема, лише в 60-х роках знайшла пояснення і була виключена з розряду емпіричних нерівність понад 9". Для низки супутників інших планет теорії руху є ще досить наближеними.

Найбільші ускладнення виникають при створенні теорій руху супутників планет, зокрема Місяця. Це пояснюється необхідністю досконалого знання гравітаційної фігури та внутрішньої будови планет, які мало вивчені. Для Місяця проблема створення теорії руху ускладнюється ще й близьким розташуванням його відносно Сонця, яке є масивним тілом і суттєво збурює рух в орбіті. Саме тому, ще в 60-70-х роках XX ст. три рази уточнювалась остання аналітична теорія руху Місяця, створена Брауном. Зокрема, лише в 60-х роках знайшла пояснення і була виключена з розряду емпіричних нерівність понад 9". Для низки супутників інших планет теорії руху є ще досить наближеними.

ДЯКУЮ
ЗА
УВАГУ!