Презентація на тему «Многогранники» (варіант 1)

ГЕОМЕТРИЧНІ ТІЛА
многогранники
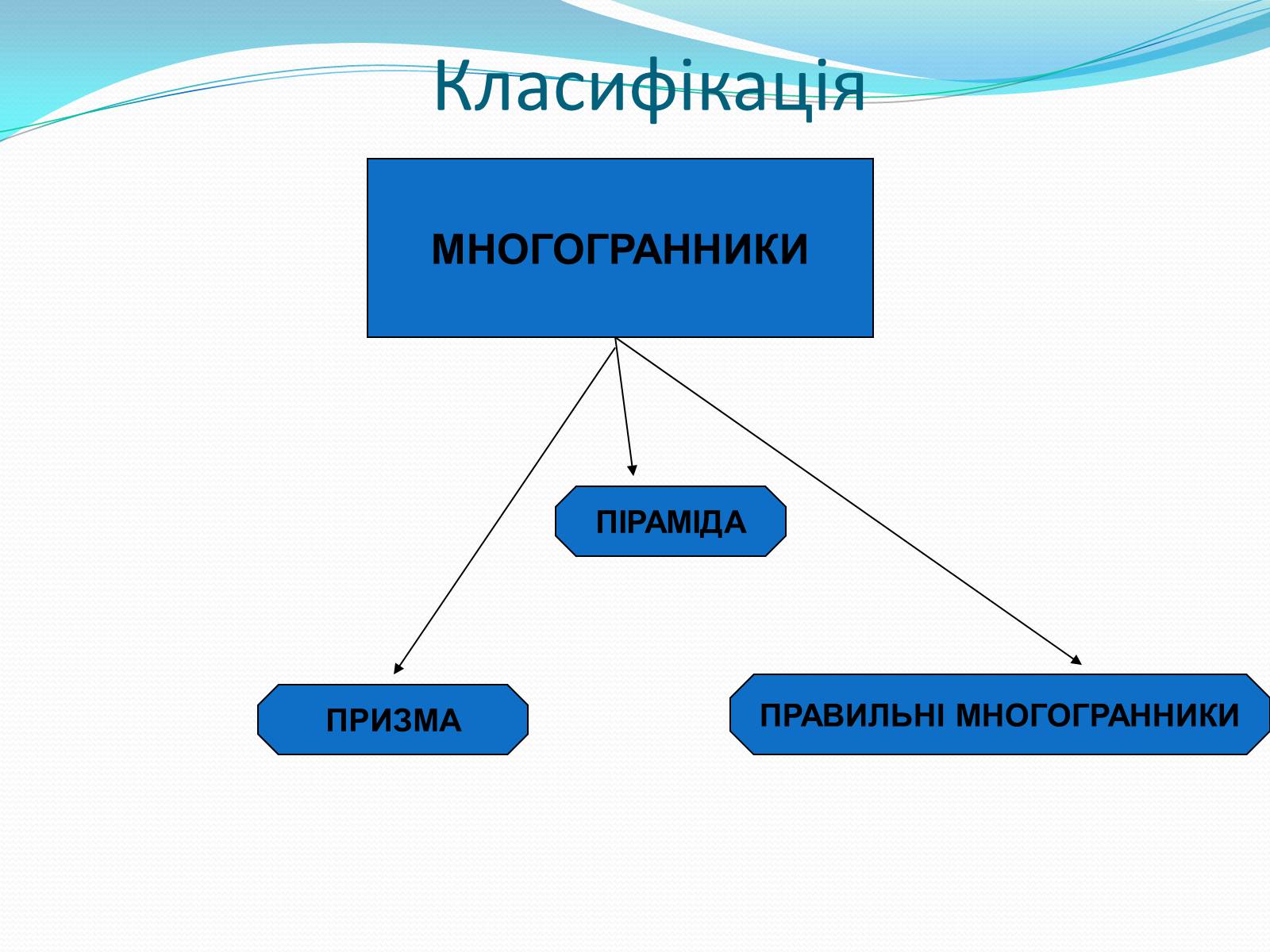
Класифікація
МНОГОГРАННИКИ
ПРИЗМА
ПІРАМІДА
ПРАВИЛЬНІ МНОГОГРАННИКИ

Поняття многогранника
Тіло, поверхня якого складається зі скінченної кількості плоских многокутників, тобто з їх внутрішніми областями, називають многогранником.
Приклади многогранників
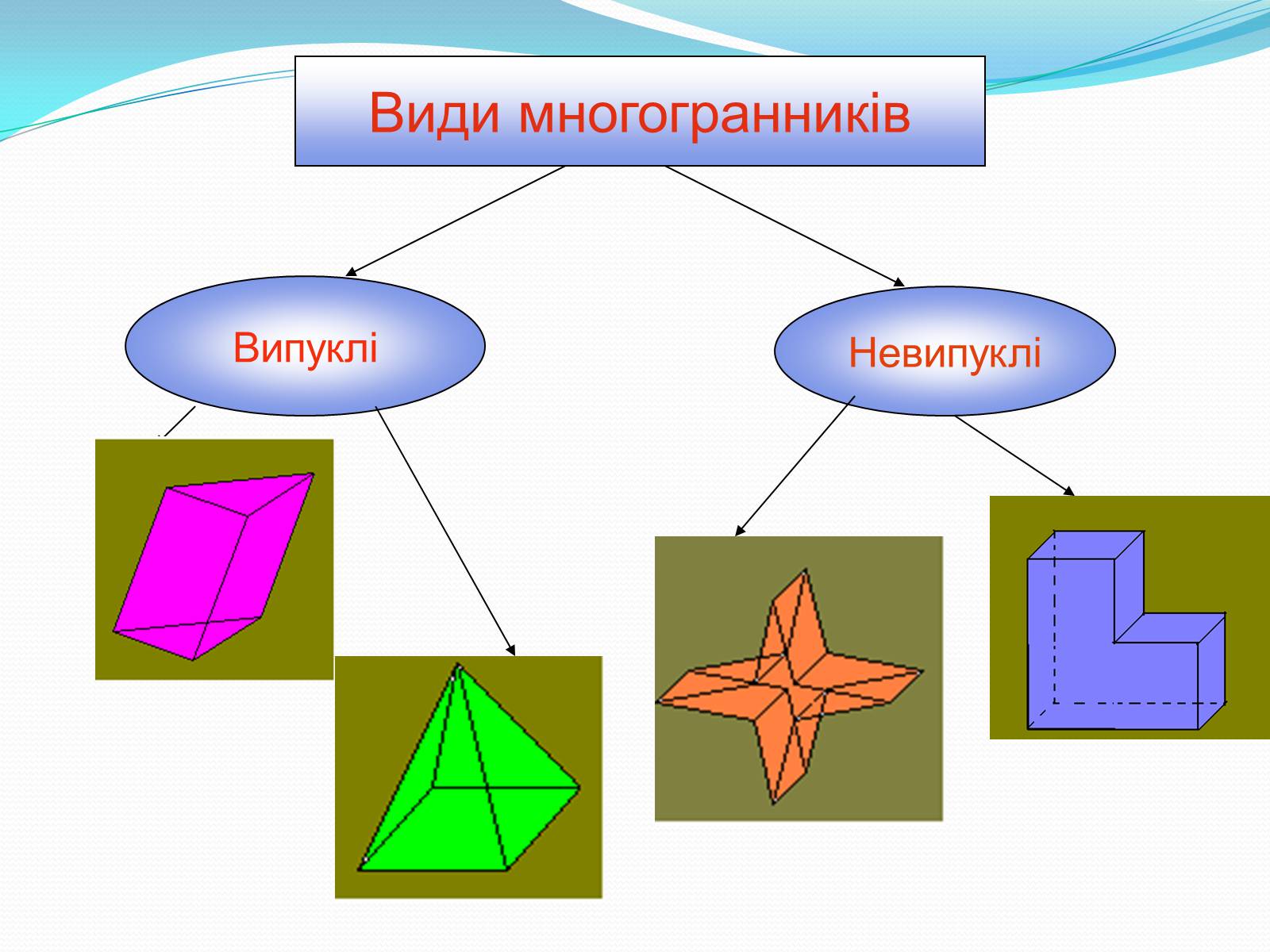
Види многогранників
Випуклі
Невипуклі

Випуклі многогранники
Многогранник називаеться випуклим, якщо він розташований по одну сторону від площини кожної його грані.
Всі грані випуклого многогранника є выпуклими многокутниками
У випуклому многограннику сума всіх плоских кутів при кожній його вершині меньше 360 градусів.
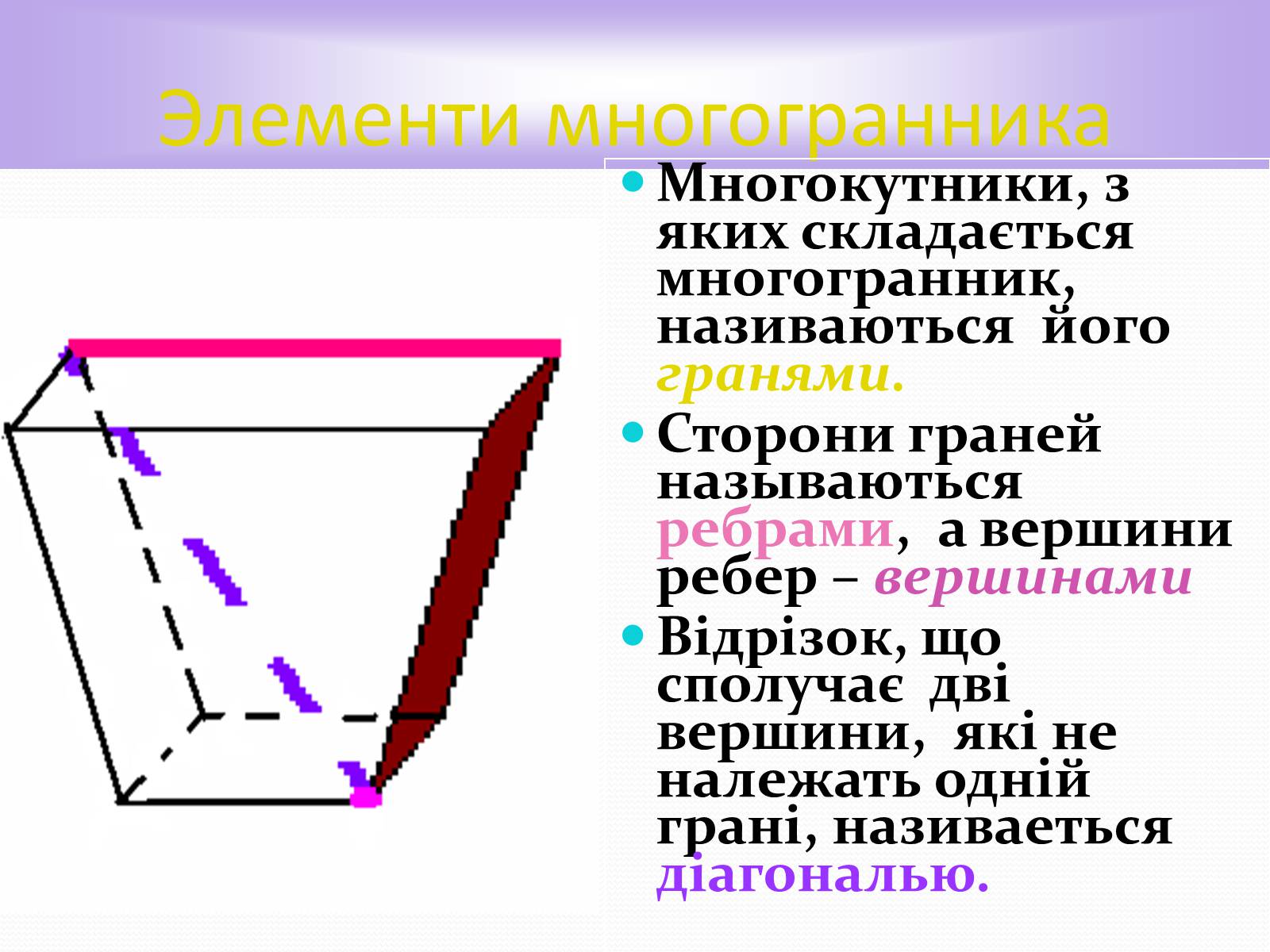
Элементи многогранника
Многокутники, з яких складається многогранник, називаються його гранями.
Сторони граней называються ребрами, а вершини ребер – вершинами
Відрізок, що сполучає дві вершини, які не належать одній грані, називаеться діагональю.
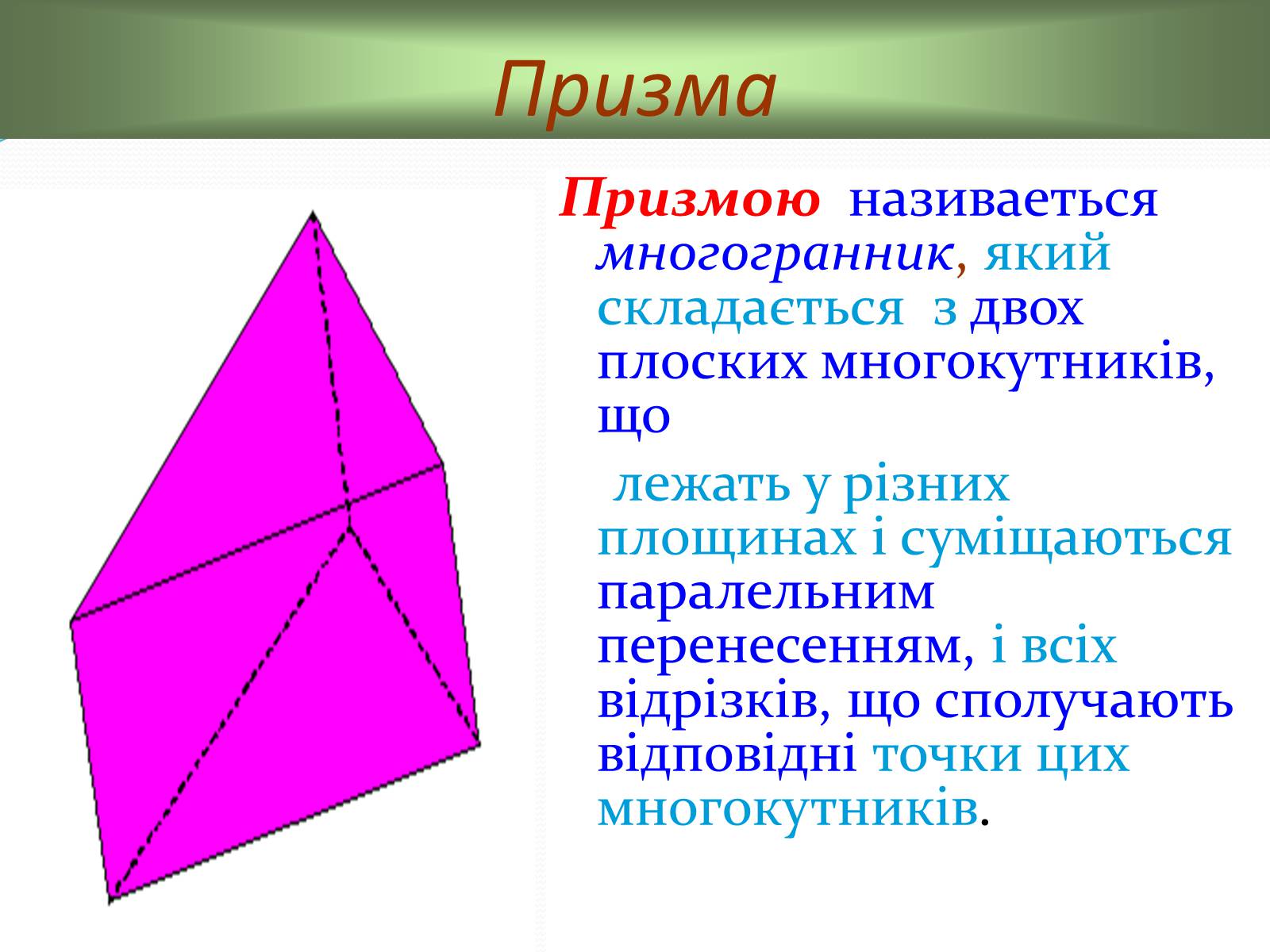
Призма
Призмою називаеться многогранник, який складається з двох плоских многокутників, що
лежать у різних площинах і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих многокутників.
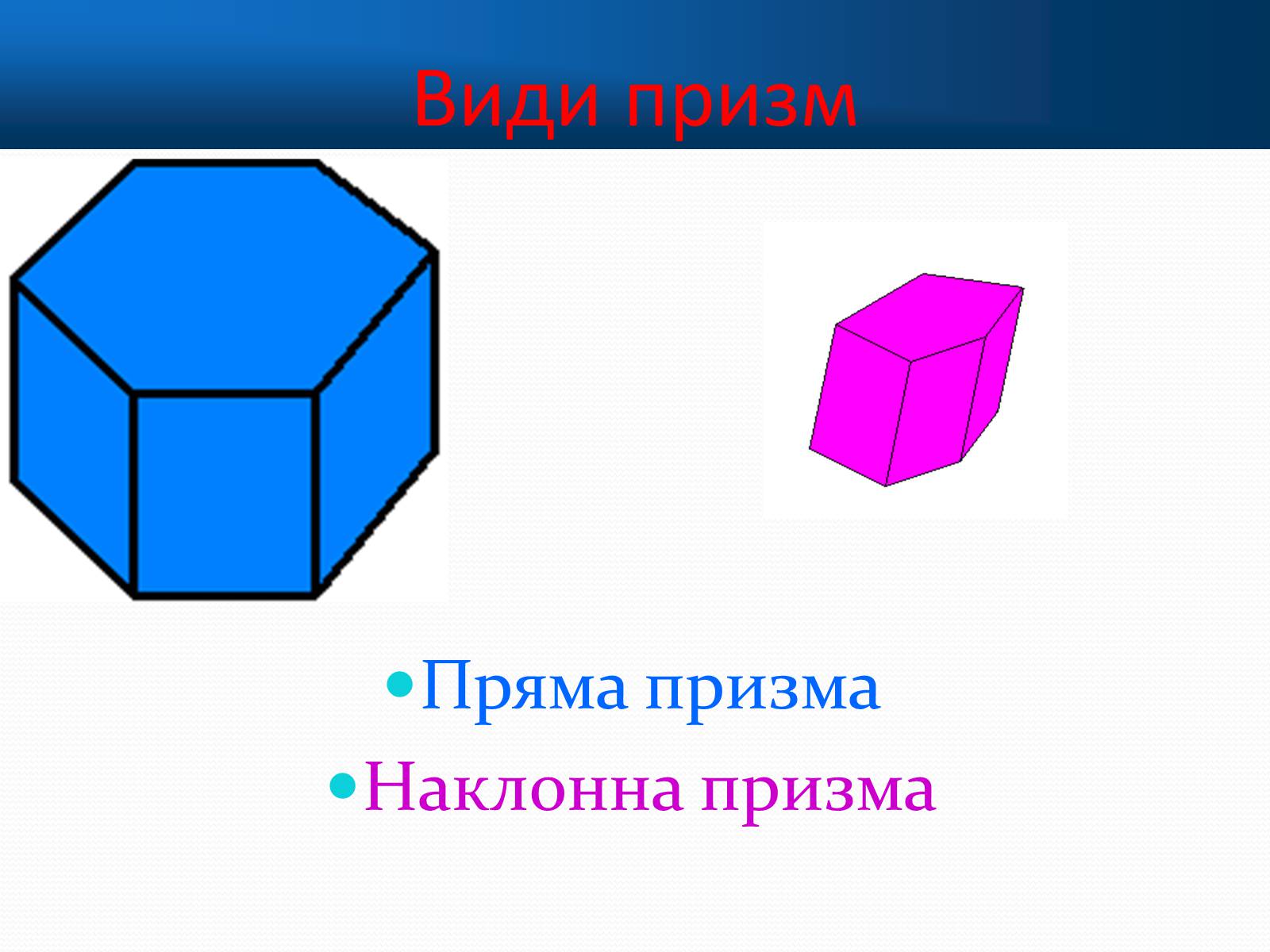
Види призм
Пряма призма
Наклонна призма

ВИЗНАЧЕННЯ
Якщо бічні ребра призми перпендикулярні до основ, то призма
называеться прямою, інакше– наклонною.
Висота прямої призми дорівню її бічному ребру.

Формула знаходження S призми
Площею повної
поверхні призми(Sповн)
називаеться сума
площ всіх її граней, а
площею бічної поверхні призми (Sбічн)-сума площ бічних її граней.
S повн = Sбічн+2S осн
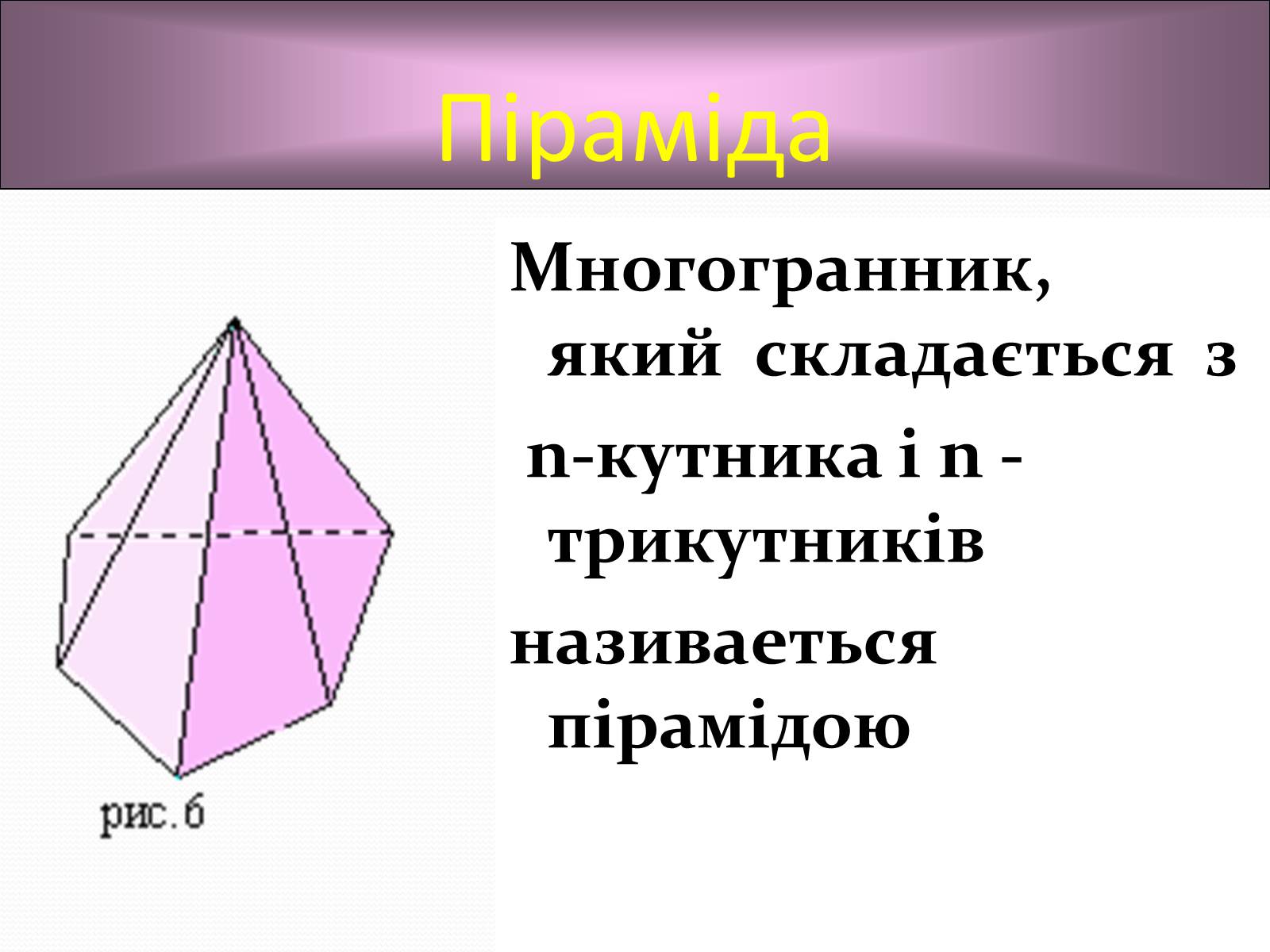
Піраміда
Многогранник, який складається з
n-кутника і n -трикутників
називаеться пірамідою
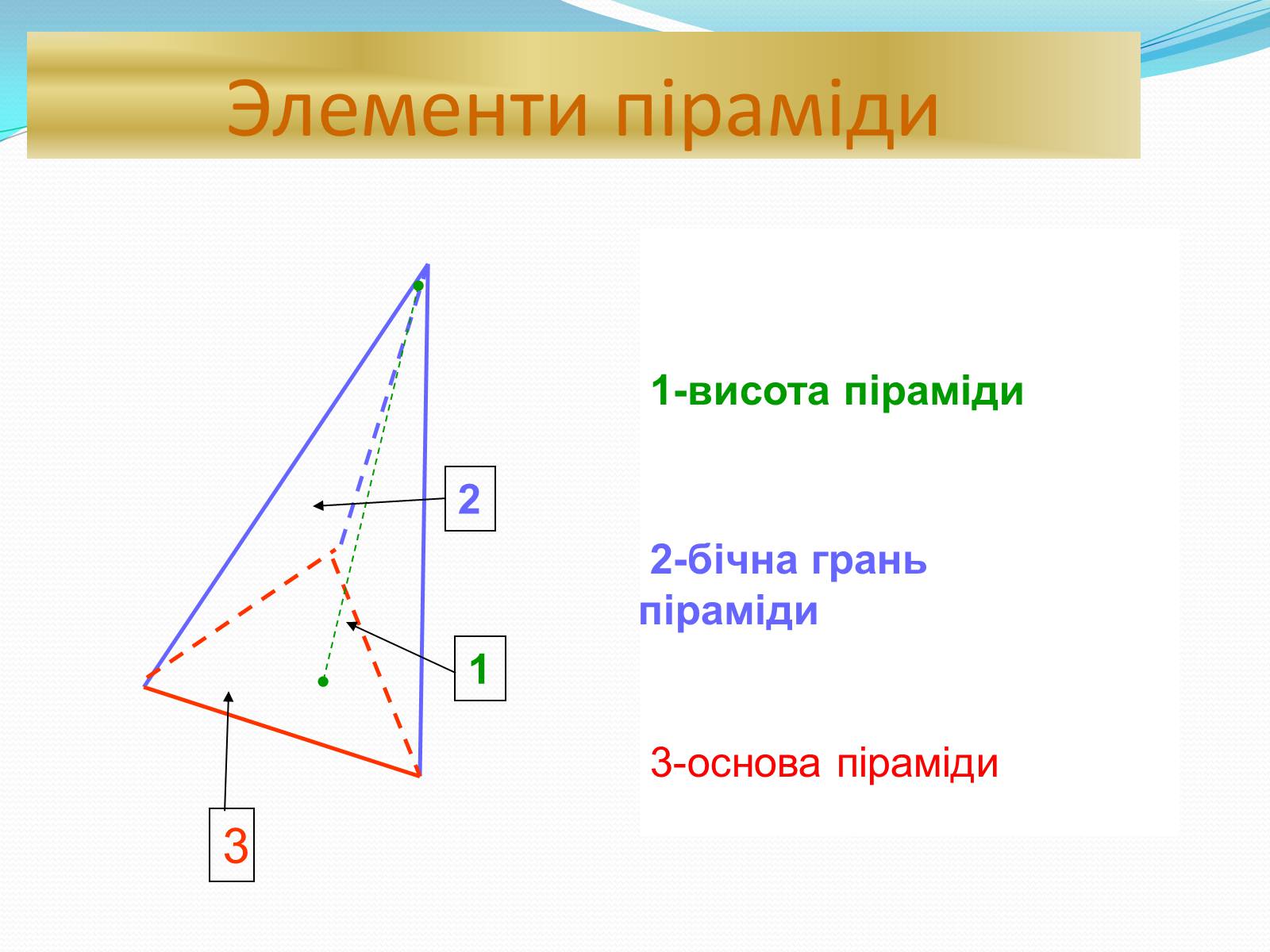
Элементи піраміди
1
2
3
1-висота піраміди
2-бічна грань піраміди
3-основа піраміди

Правильні многогранники
Випуклий многогранник називаеться
правильним, якщо всі його грані– рівні
правильні многокутники і в кажній його
вершині сходиться одне і те ж саме число
ребер.
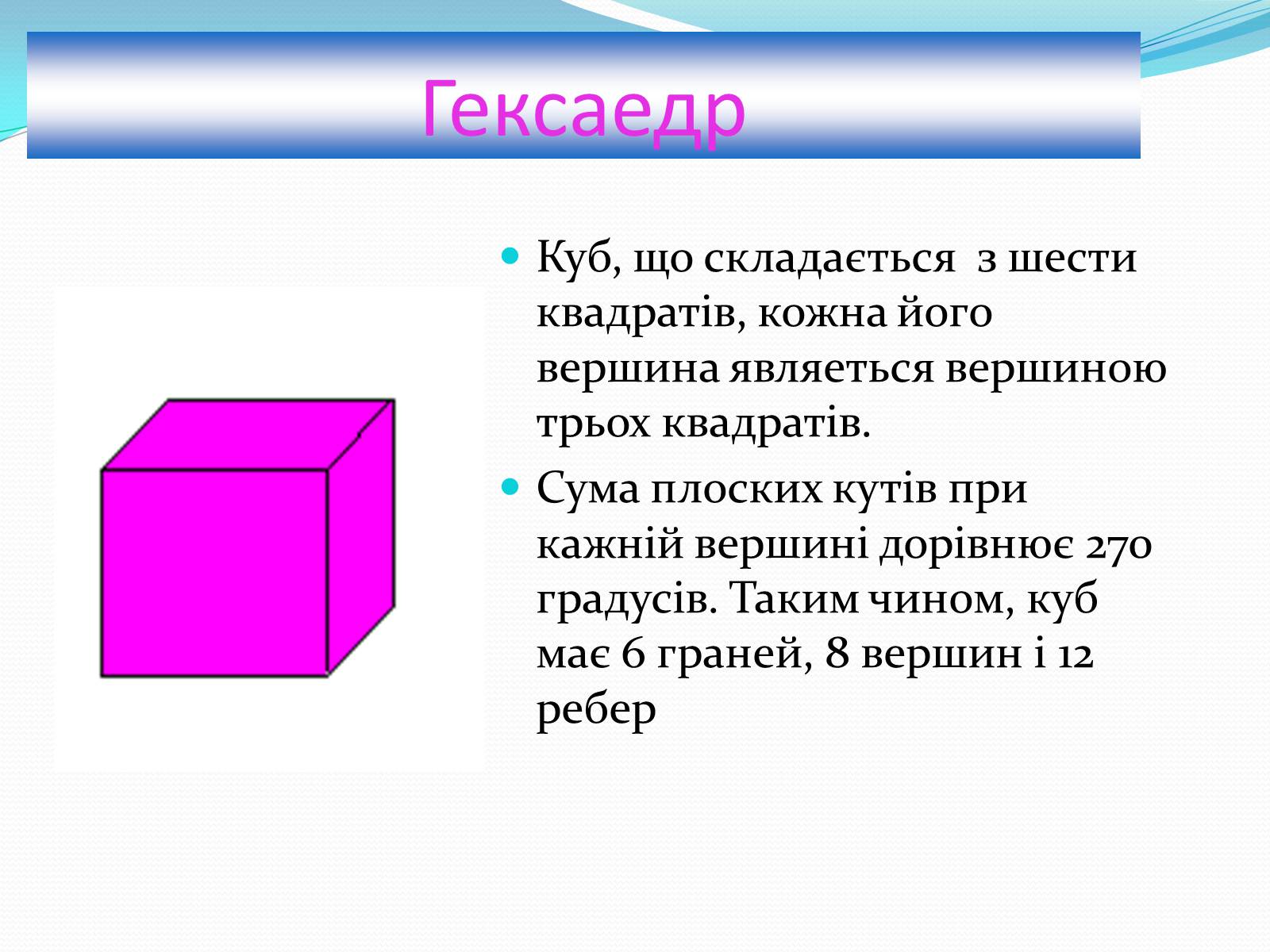
Гексаедр
Куб, що складається з шести квадратів, кожна його вершина являеться вершиною трьох квадратів.
Сума плоских кутів при кажній вершині дорівнює 270 градусів. Таким чином, куб має 6 граней, 8 вершин і 12 ребер

Основні формули для гексаедра
Визначення:
а – ребро,
V-об'эм,
S-площа бічної поверхні,
R-радіус описаної сфери,
r- радіус вписаної сфери,
H- висота.

Тетраедр
Тетраедр складений з чотирьох рівносторонніх трикутників.
Кожна йго вершина являеться вершиною трьох трикутників.
Сума плоских кутів при кожній вершині дорівнює 180 градусів.
Таким чином, тетраедр має 4 грані, 4 вершини і 6 ребер.

Основні формули для тетраедра
Визначення:
а – ребро,
V-об'єм,
S-площа бічної поверхні,
R-радіус описанної сфери,
r- радіус вписанної сфери,
H- висота.
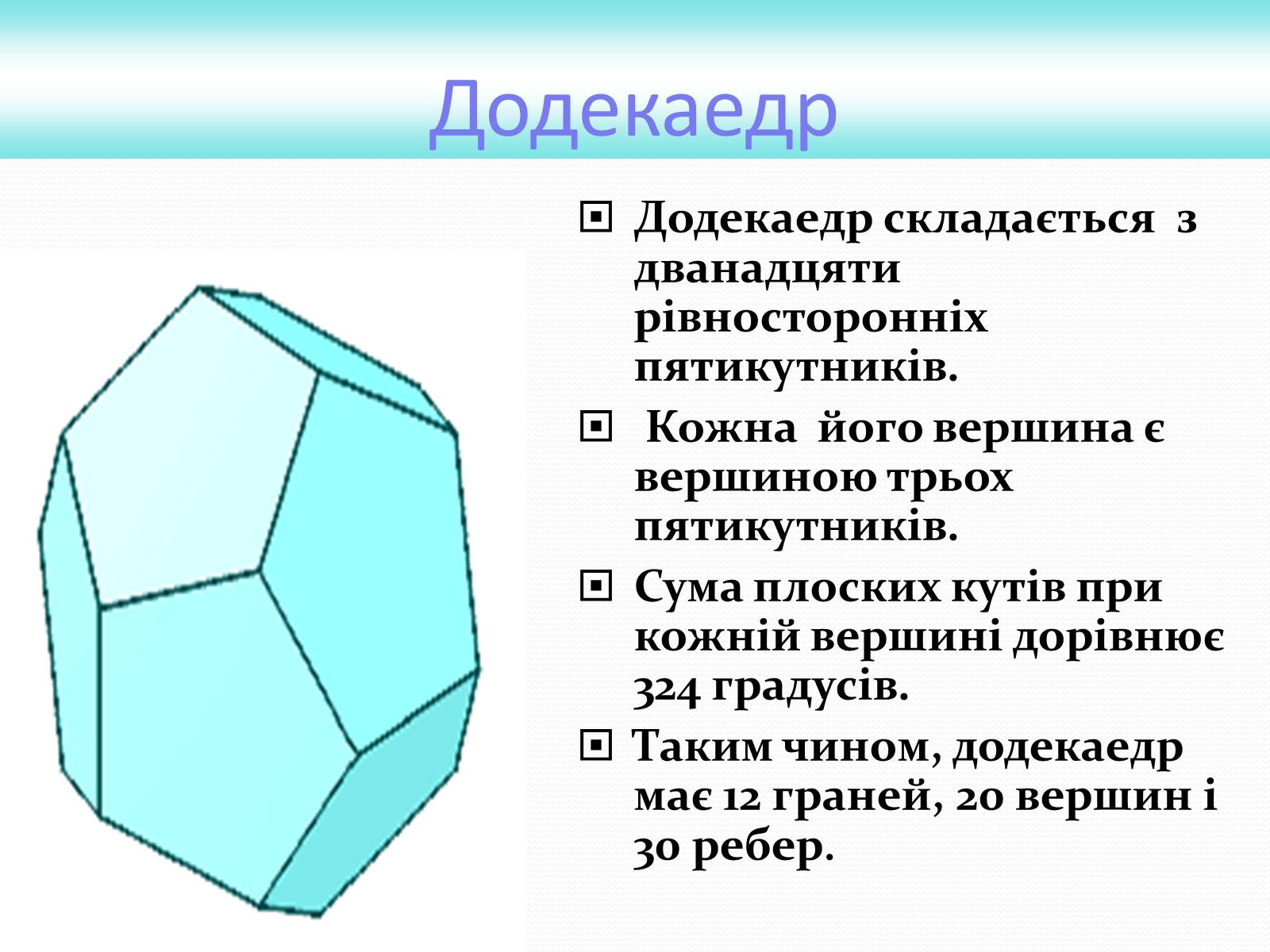
Додекаедр
Додекаедр складається з дванадцяти рівносторонніх пятикутників.
Кожна його вершина є вершиною трьох пятикутників.
Сума плоских кутів при кожній вершині дорівнює 324 градусів.
Таким чином, додекаедр має 12 граней, 20 вершин і 30 ребер.

Основні формули для додекаедра
Визначення:
а – ребро,
V-об'єм,
S-площа бічної поверхні,
R-радіус описаної сфери,
r- радіус вписаної сфери,
H- висота.

Тест №1
Геометричне тіло, поверхня якого складається із скінченого числа плоских многокутників називається:
А) чотирикутник
В) многогранник
С) призма

Тест№2
Частини площин (многокутники), які обмежують многогранник:
А) вершина
В) діагональ
С) ребра
Д) грань

Тест№3Виберіть ознаку, яка не відноситься до випуклих многогранників
А) Многогранник називаеться випуклим, якщо він розташований по одну сторону від площини кожної його грані.
В) Всі грані випуклого многогранника є выпуклими многокутниками
Г) У випуклому многограннику сума всіх плоских кутів при кожній його вершині меньше 180 градусів.
Д) У випуклому многограннику сума всіх плоских кутів при кожній його вершині меньше 360 градусів.

Тест№4Що називається висотою піраміди?
А) відрізок, що сполучає вершину піраміди з основою
В) відрізок, проведений з вершини піраміди до протилежної сторони, який ділить її навпіл
С) перпендикуляр, опущений із вершини піраміди на площину основи.
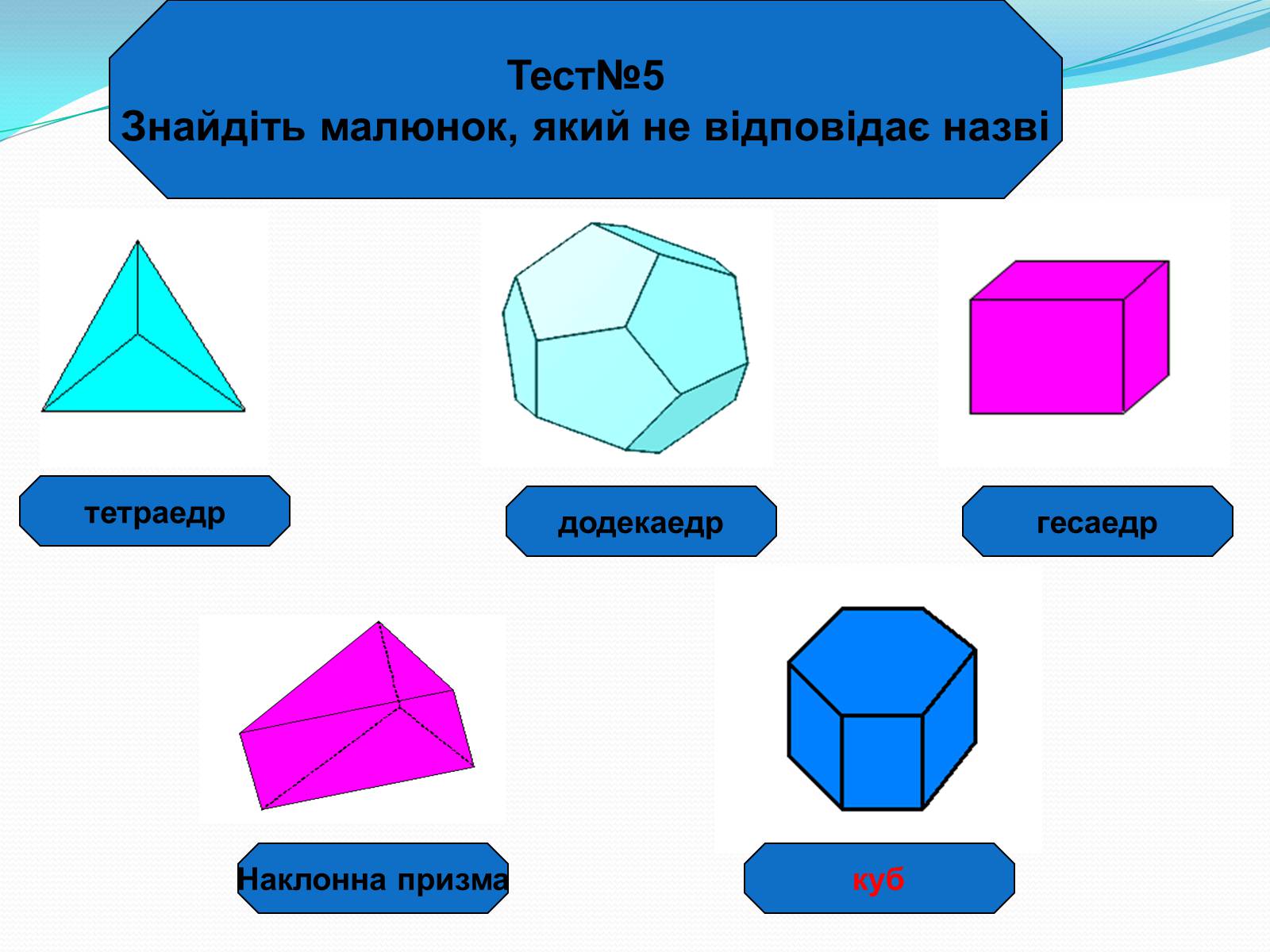
гесаедр
Тест№5
Знайдіть малюнок, який не відповідає назві
додекаедр
тетраедр
Наклонна призма
куб

Молодець
тест№1 тест№2 тест№3 тест№4 тест№5

Невдаха
Спробуй ще !!!
Тест№1 тест№2 тест№3 тест№4 тест№5