Презентація на тему «Лабіринти»

Лабіринти
Підготували
учні 10 класу
Макарівського НВК Ківа Анастасіята Ніколаєв Артем
Керівник Показій А.П.

План:
Справка
Математична сторона
Правило ”руки”
Загальна схема
Теорія графів
Використані джерела
Висновок

Справка
Коли, де і навіщо люди почали
створювати лабіринти історії не відомо. Але вони завжди мали велике філософське та культурне значення.Зустріти їх можна від пірамід Єгипту до парків і соборів Європи, від античності до наших днів.

Лабіринтами в давнину в Греції і Єгипті називали споруди зі складними заплутаними ходами, в які легко потрапити, і дуже важко вибратися. Уперше про один з них повідомив давньогрецький історик Геродот. У другій книжці свого знаменитого твору «ІСТОРІЯ», він описав відвіданий ним велетенський Фаюмський лабіринт і розповів про історію його побудови.
Цей найдавніший з відомих лабіринтів був заупокійним храмом, побудованим біля піраміди фараона Аменемхета III (1840--1792 р. до. н.е.).

В одному з найчарівніших давньогрецьких міфів розповідається про лабіринт крітського царя Міноса. Цю споруду вважають одним із семи чудес світу. У лабіринті Мінос переховував чудовисько, яке живилося людським м'ясом.
Син афінського царя Егея сміливий Тезей вирішив звільнити рідне місто від кривавої данини. Разом з юнаками і дівчатами, приреченими на жертву, він поплив на о. Кріт. Дочка Міноса Аріадна полюбила героя і взялася допомогти йому. Вона вручила Тезею меч і клубок ниток. Закріпивши кінець нитки біля входу, Тезей, блукаючи в лабіринті, розмотував нитку, чим позначав пройдений шлях. Герой зустрів чудовисько і в тяжкому поєдинку вбив його, а за ниткою Аріадни знайшов вихід із зачарованого палацу. Звідси й широко відомі метафори -- «лабіринт» -- безвихідне становище, заплутана ситуація, з якої немає розумного виходу і «аріаднина нитка» -- правильне розв'язання складної за дачі, щаслива ідея в заплутаній ситуації тощо.

Вивчення властивостей мереж сходить до робіт видатного математика XVIII століття Леонарда Ейлера. Розглянемо довільну мережу. Вузол називається парним або непарним залежно від того, скільки сходиться в ньому гілок. Маршрут - це будь-яка послідовність гілок, в якій жодна з гілок не повторюється. Замкнутий маршрут закінчується в тому ж вузлі, де й починається. Назвемо маршрут осяжний, якщо, слідуючи по ньому, можна обійти всю мережу, не проходячи двічі по одній гілці.
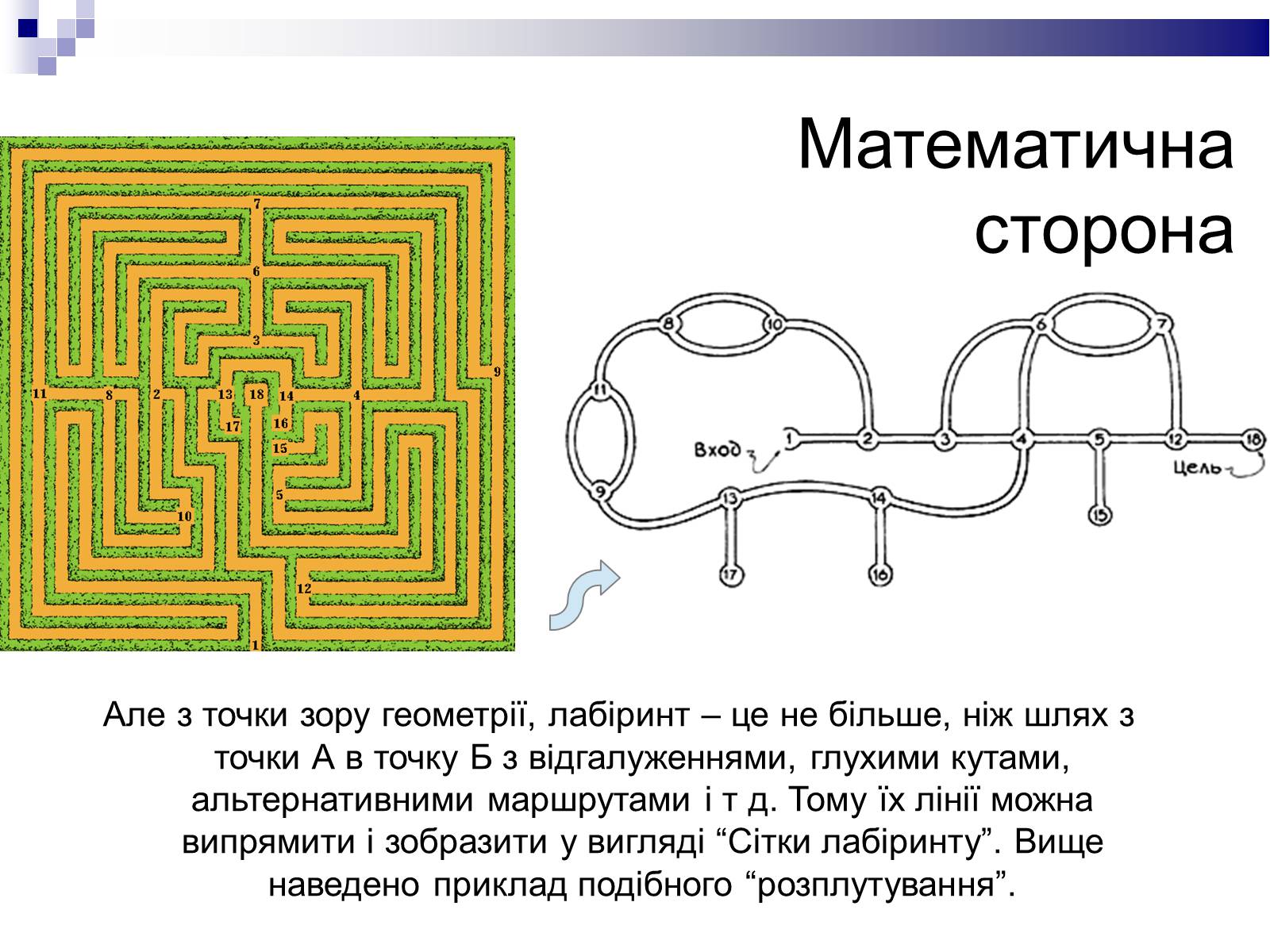
Математична сторона
Але з точки зору геометрії, лабіринт – це не більше, ніж шлях з точки А в точку Б з відгалуженнями, глухими кутами, альтернативними маршрутами і т д. Тому їх лінії можна випрямити і зобразити у вигляді “Сітки лабіринту”. Вище наведено приклад подібного “розплутування”.
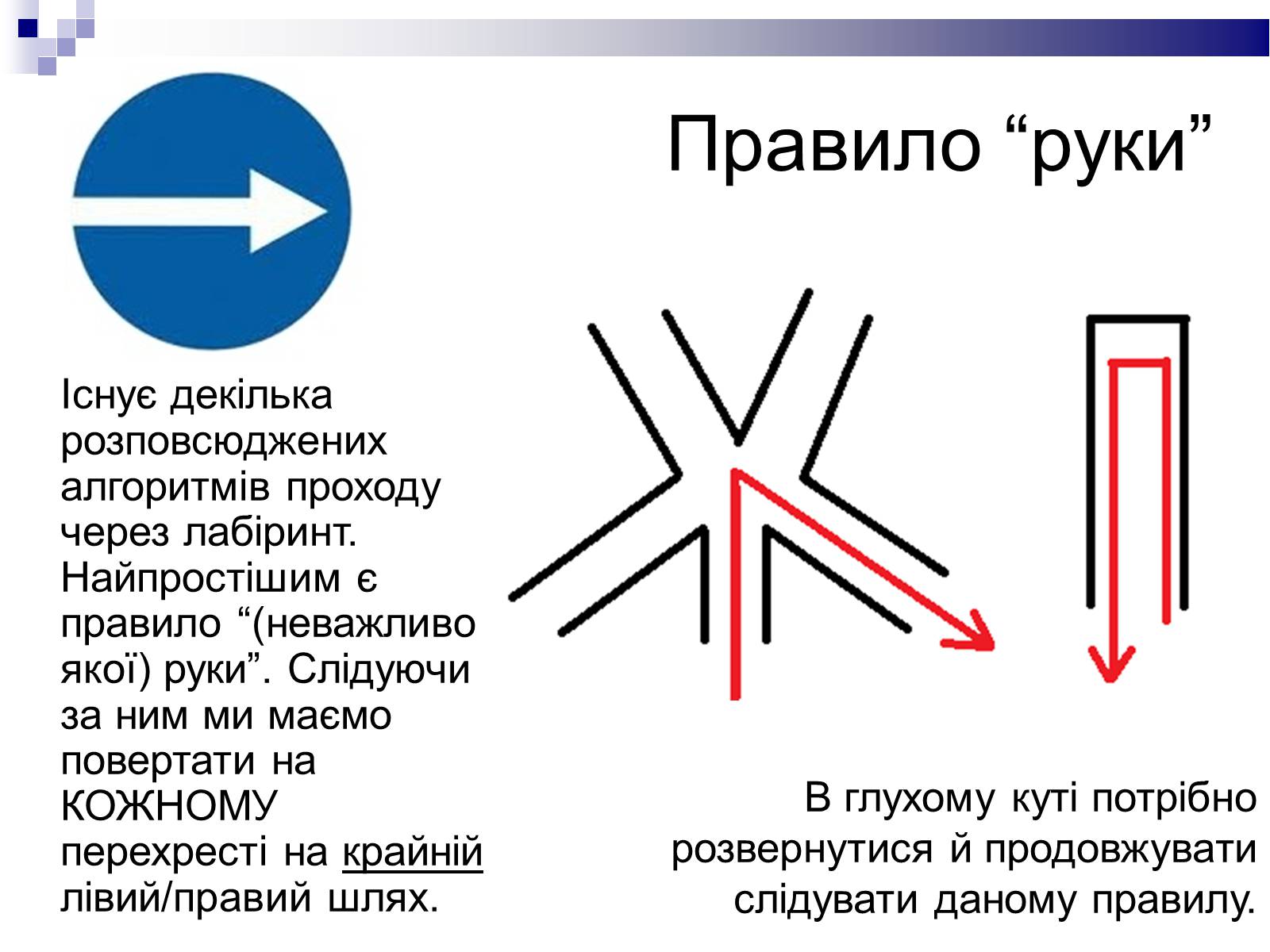
Правило “руки”
Існує декілька розповсюджених алгоритмів проходу через лабіринт. Найпростішим є правило “(неважливо якої) руки”. Слідуючи за ним ми маємо повертати на КОЖНОМУ перехресті на крайній лівий/правий шлях.
В глухому куті потрібно розвернутися й продовжувати слідувати даному правилу.
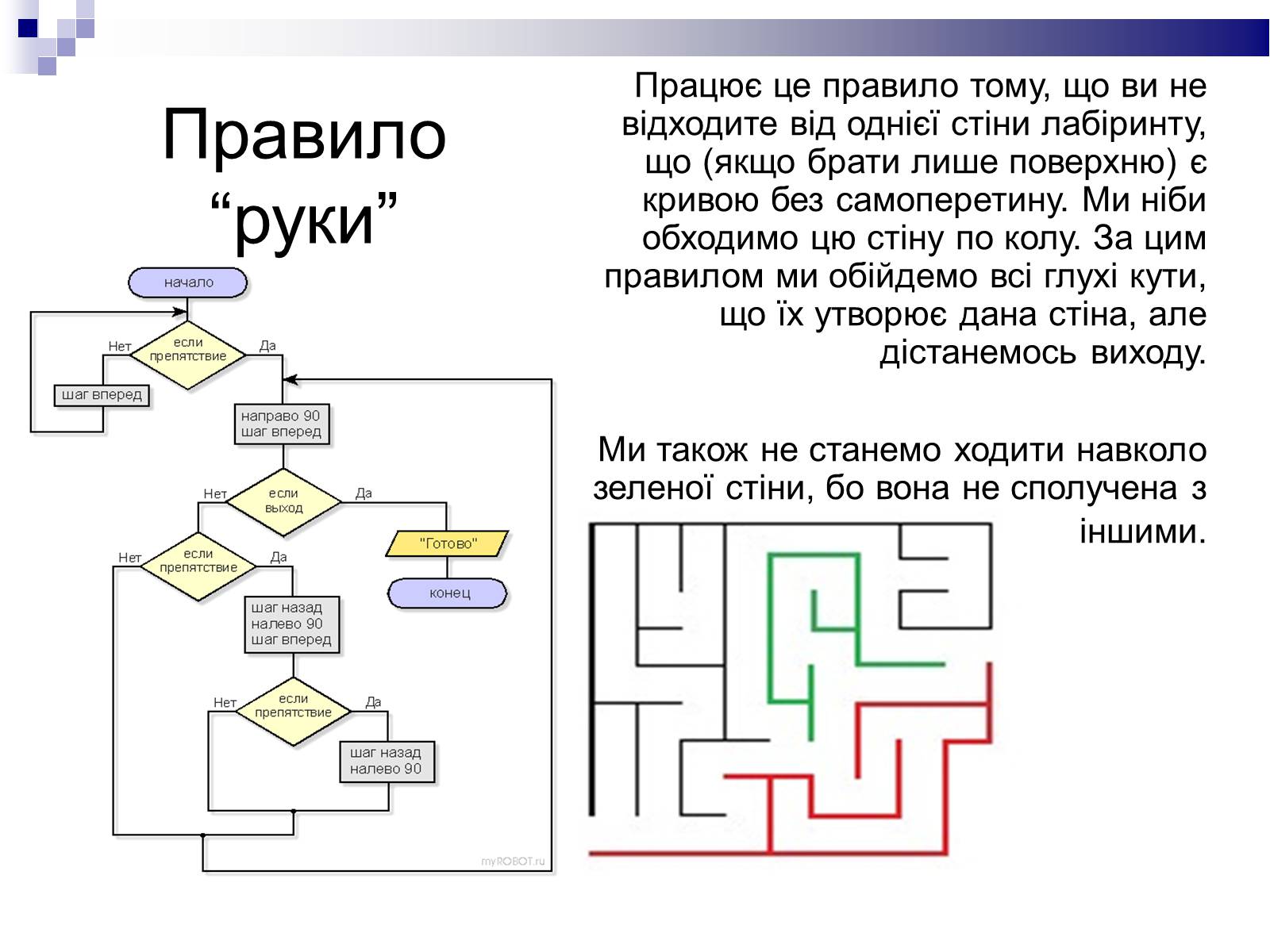
Правило “руки”
Працює це правило тому, що ви не відходите від однієї стіни лабіринту, що (якщо брати лише поверхню) є кривою без самоперетину. Ми ніби обходимо цю стіну по колу. За цим правилом ми обійдемо всі глухі кути, що їх утворює дана стіна, але дістанемось виходу.
Ми також не станемо ходити навколо зеленої стіни, бо вона не сполучена з іншими.
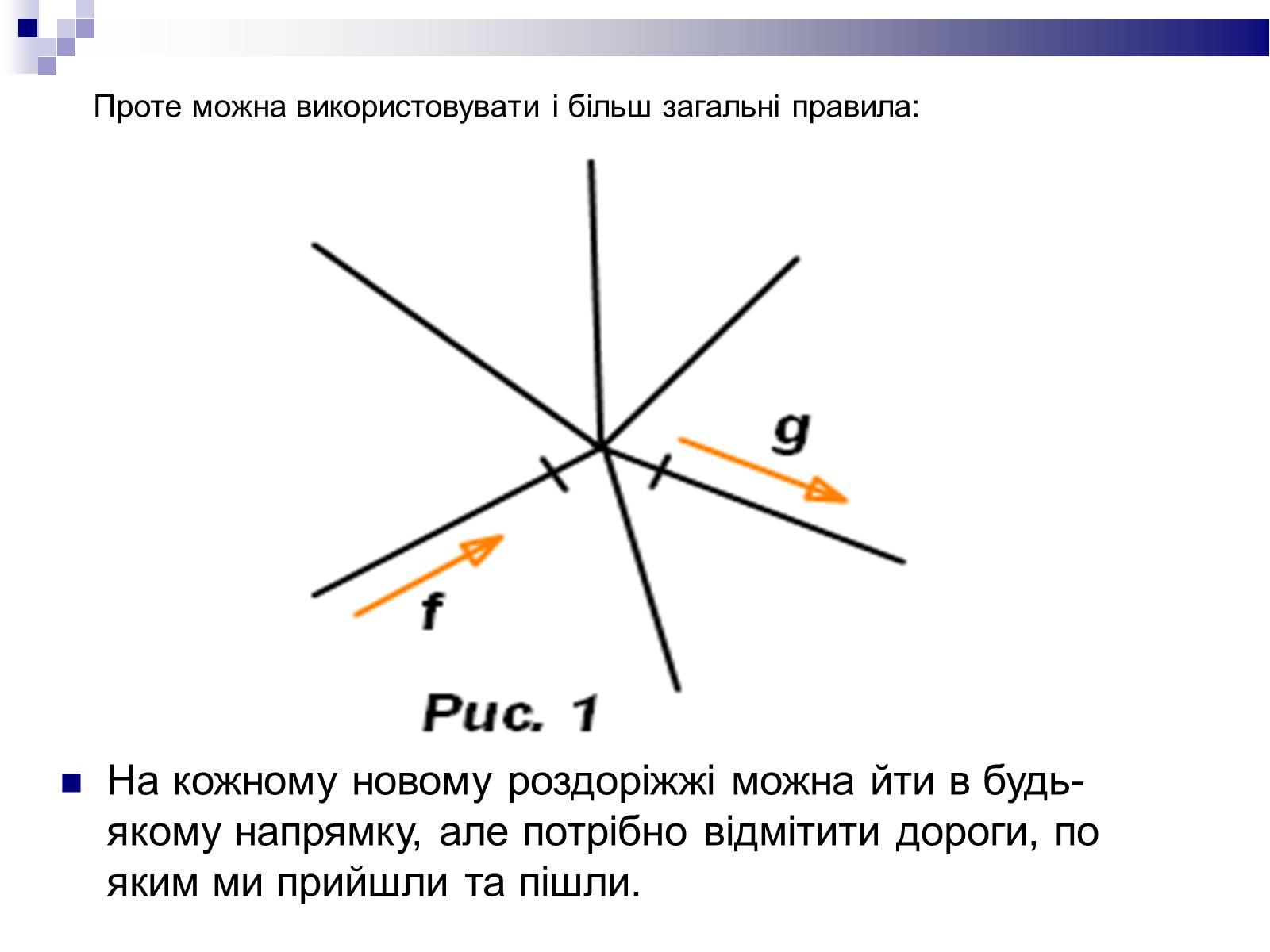
На кожному новому роздоріжжі можна йти в будь-якому напрямку, але потрібно відмітити дороги, по яким ми прийшли та пішли.
Проте можна використовувати і більш загальні правила:
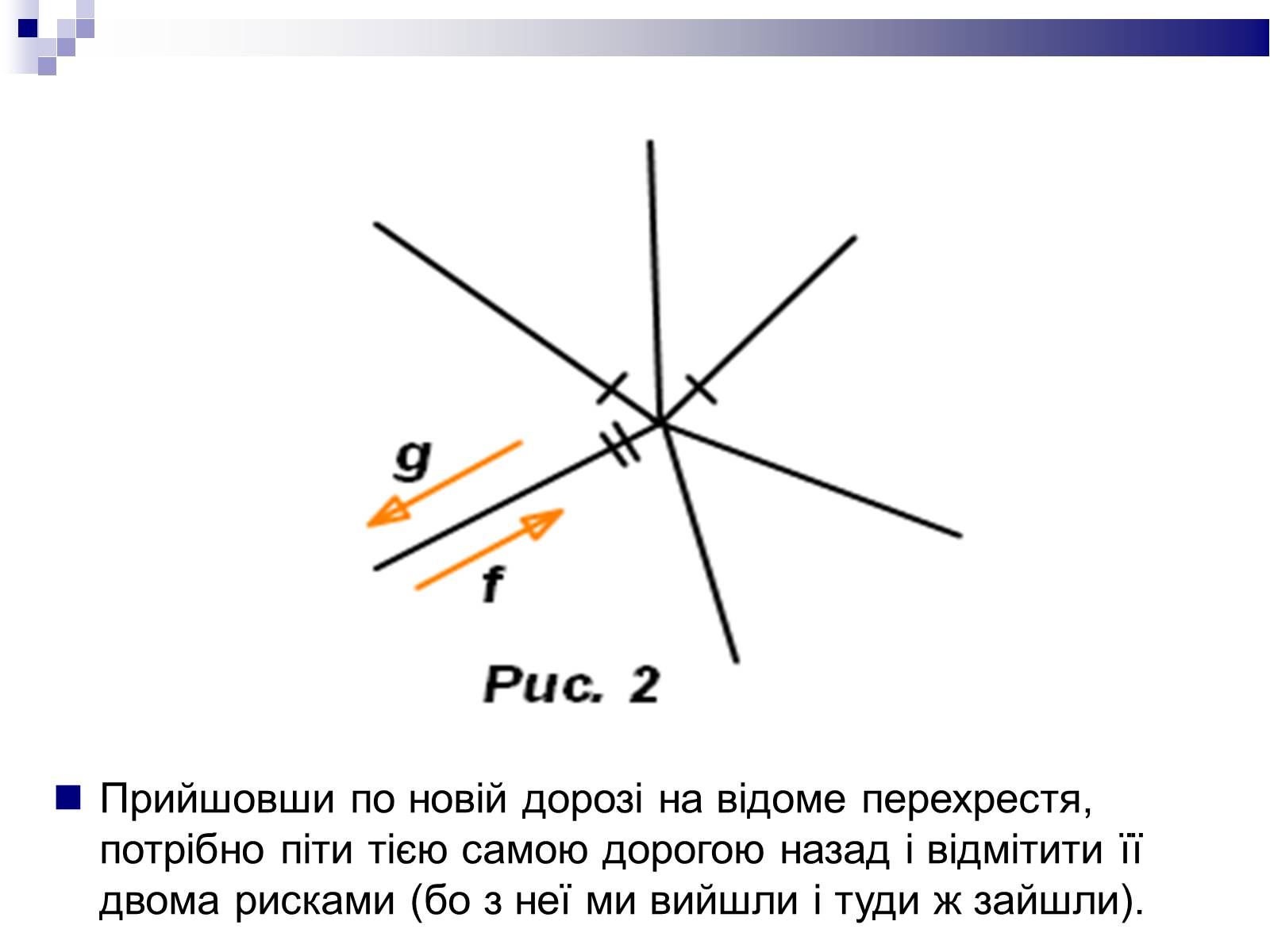
Прийшовши по новій дорозі на відоме перехрестя, потрібно піти тією самою дорогою назад і відмітити її двома рисками (бо з неї ми вийшли і туди ж зайшли).
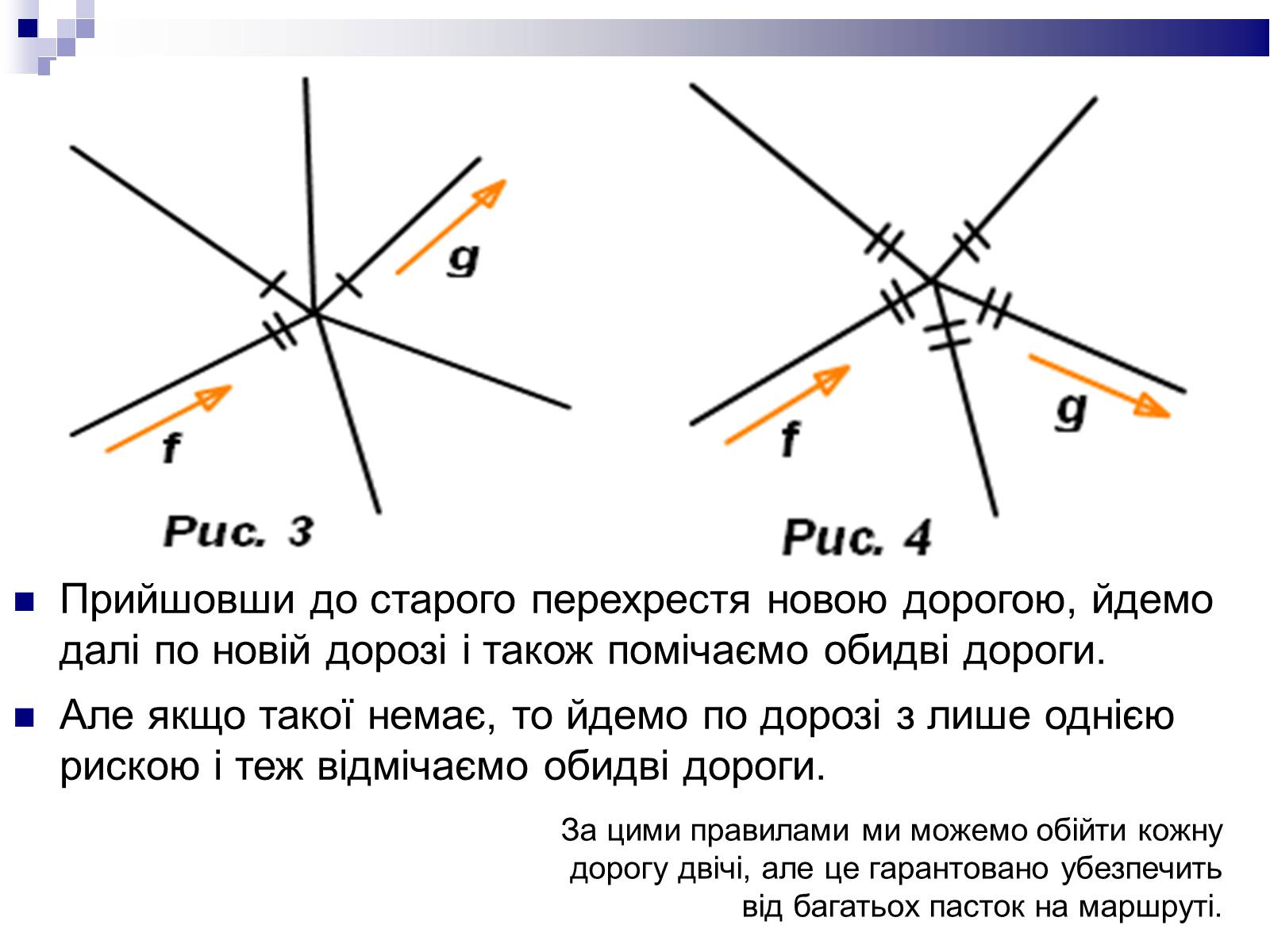
Прийшовши до старого перехрестя новою дорогою, йдемо далі по новій дорозі і також помічаємо обидві дороги.
Але якщо такої немає, то йдемо по дорозі з лише однією рискою і теж відмічаємо обидві дороги.
За цими правилами ми можемо обійти кожну дорогу двічі, але це гарантовано убезпечить від багатьох пасток на маршруті.
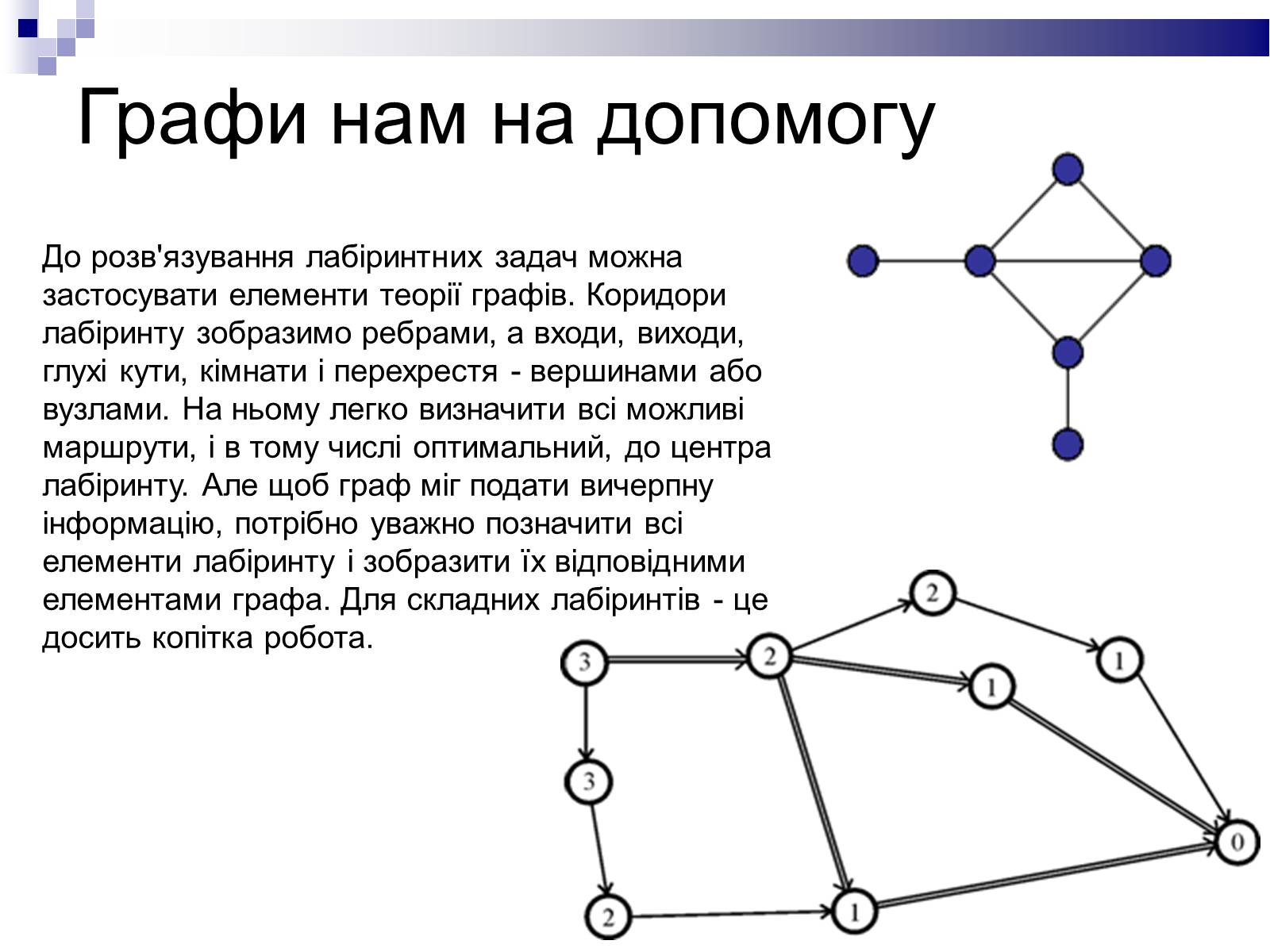
Графи нам на допомогу
До розв'язування лабіринтних задач можна застосувати елементи теорії графів. Коридори лабіринту зобразимо ребрами, а входи, виходи, глухі кути, кімнати і перехрестя - вершинами або вузлами. На ньому легко визначити всі можливі маршрути, і в тому числі оптимальний, до центра лабіринту. Але щоб граф міг подати вичерпну інформацію, потрібно уважно позначити всі елементи лабіринту і зобразити їх відповідними елементами графа. Для складних лабіринтів - це досить копітка робота.
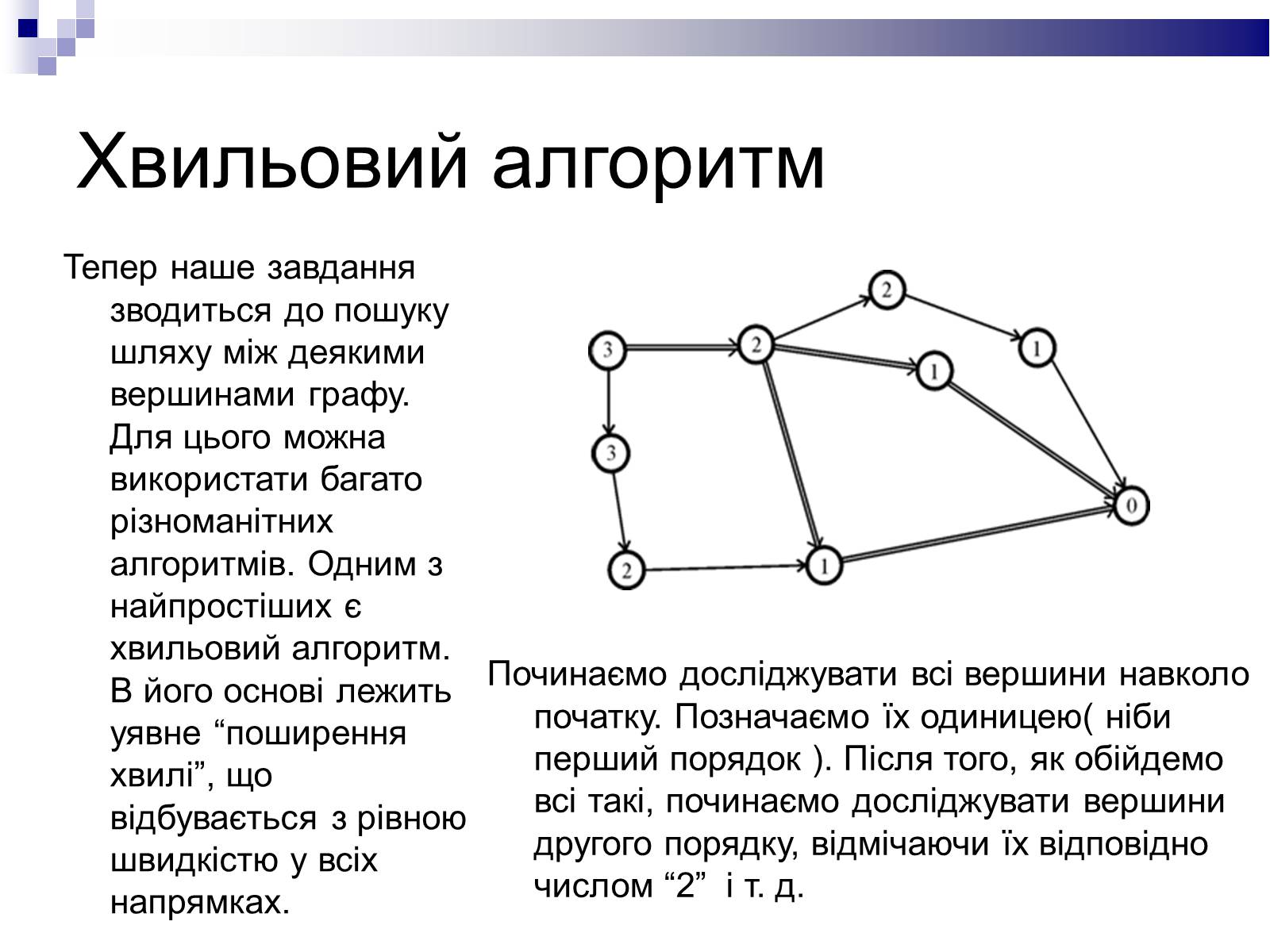
Хвильовий алгоритм
Починаємо досліджувати всі вершини навколо початку. Позначаємо їх одиницею( ніби перший порядок ). Після того, як обійдемо всі такі, починаємо досліджувати вершини другого порядку, відмічаючи їх відповідно числом “2” і т. д.
Тепер наше завдання зводиться до пошуку шляху між деякими вершинами графу. Для цього можна використати багато різноманітних алгоритмів. Одним з найпростіших є хвильовий алгоритм. В його основі лежить уявне “поширення хвилі”, що відбувається з рівною швидкістю у всіх напрямках.
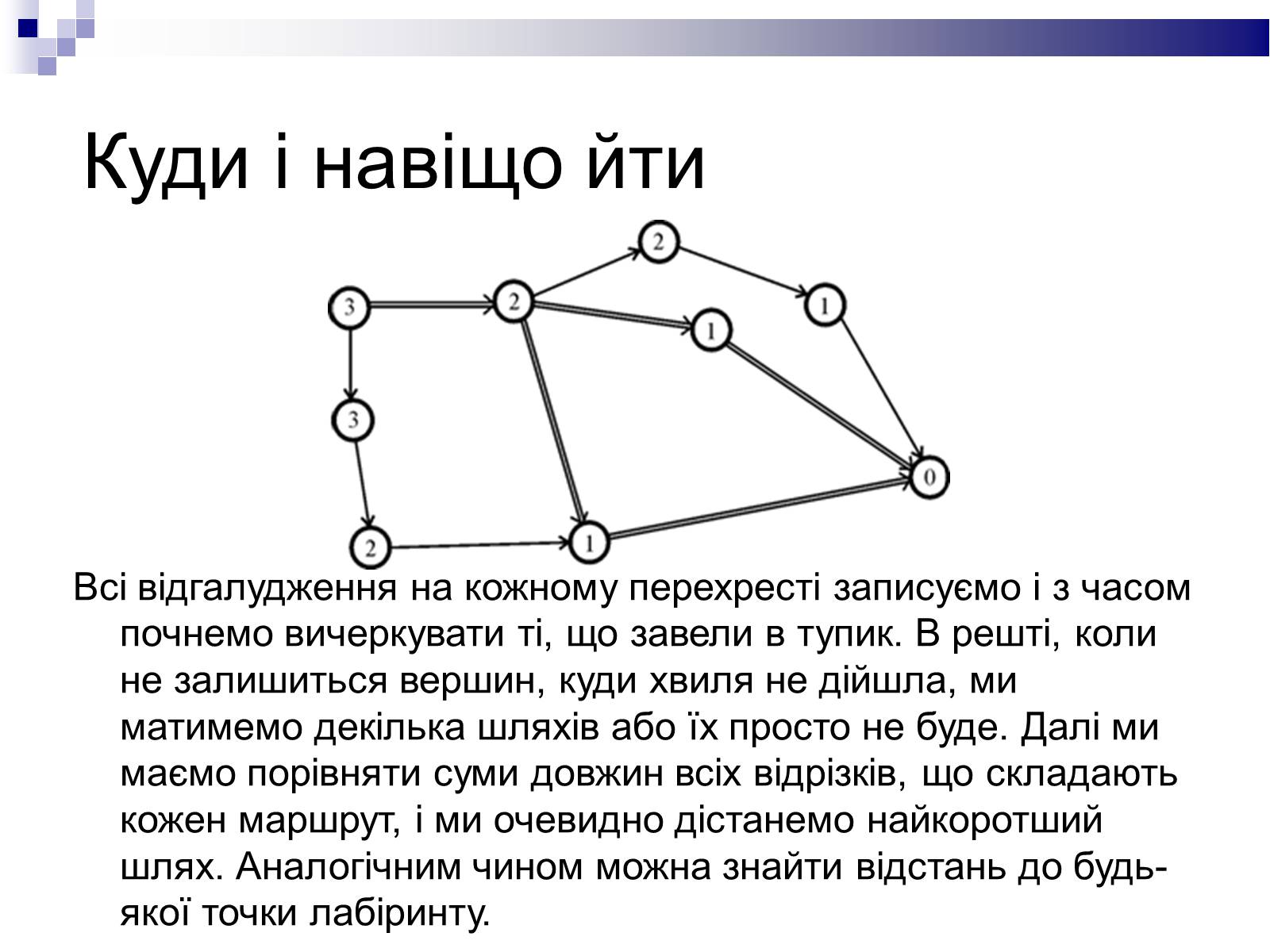
Куди і навіщо йти
Всі відгалудження на кожному перехресті записуємо і з часом почнемо вичеркувати ті, що завели в тупик. В решті, коли не залишиться вершин, куди хвиля не дійшла, ми матимемо декілька шляхів або їх просто не буде. Далі ми маємо порівняти суми довжин всіх відрізків, що складають кожен маршрут, і ми очевидно дістанемо найкоротший шлях. Аналогічним чином можна знайти відстань до будь-якої точки лабіринту.

Висновок
Лабіринт — це тяжкопрохідний і неясний шлях, на складних та звивистих стежках. Але кожен з них піддається ґрунтовному математичному опису. Знаючи відповідні прийоми ми можемо легко знайти вихід та дістатися будь-якої точки. Використати це можна як при мандрівці реальною спорудою, так і при розв'язуванні задач. Якщо ви захоплюєтеся програмуванням, то з легкістю зможете знайти ще багато “продвинутих” алгоритмів, що спростять задачу ще більше.

Використані джерела
http://uk.wikipedia.org/wiki/%D0%9B%D0%B0%D0%B1%D1%96%D1%80%D0%B8%D0%BD%D1%82
http://www.0zd.ru/matematika/labirinti.html
http://formula.co.ua/blog/bezvyhidnyh-labiryntiv-nemaje/
http://uk.wikipedia.org/wiki/%D0%93%D1%80%D0%B0%D1%84_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)
http://ua-referat.com/%D0%9F%D0%BE%D1%88%D1%83%D0%BA_%D0%BD%D0%B0%D0%B9%D0%BA%D0%BE%D1%80%D0%BE%D1%82%D1%88%D0%BE%D0%B3%D0%BE_%D1%88%D0%BB%D1%8F%D1%85%D1%83_%D0%B2_%D0%BB%D0%B0%D0%B1%D1%96%D1%80%D0%B8%D0%BD%D1%82%D1%96
... ну і звісно ж Google
http://uk.wikipedia.org/wiki/%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B0_%D0%BF%D1%80%D0%BE_%D0%BD%D0%B0%D0%B9%D0%BA%D0%BE%D1%80%D0%BE%D1%82%D1%88%D0%B8%D0%B9_%D1%88%D0%BB%D1%8F%D1%85
http://uk.wikipedia.org/wiki/%D0%A5%D0%B2%D0%B8%D0%BB%D1%8C%D0%BE%D0%B2%D0%B8%D0%B9_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC
http://my5.com.ua/archives/430
http://ega-math.narod.ru/Nquant/Maze.htm
http://refs.co.ua/65419-Algoritmy_trassirovki.html

The End =)