Презентація на тему «Показательные уравнения и неравенства»

Тема:Показательные уравнения и неравенства

Это уравнение, в котором неизвестные и выражения с ними находятся в показателях каких-то степеней. И только там! Это важно.
Вот вам примеры показательных уравнений:
5х+2 = 125
3х·2х = 8х+3
32х+4·3х-5 = 0
И так далее…
Что такое показательное уравнение?
Обратите внимание! В основаниях степеней (внизу) - только числа. В показателях степеней (вверху) - самые разнообразные выражения с иксом.

Решение простейших показательных уравнений.
Для начала решим что-нибудь совсем элементарное. Например:
3х = 32
х = 2
Что мы сделали? Мы, фактически, просто отбросили одинаковые основания (тройки).
Действительно, если в показательном уравнении слева и справа стоят одинаковые числа в каких угодно степенях, то можно приравнять показатели степеней.

Однако, запомним: убирать основания можно только тогда, когда слева и справа числа-основания находятся в гордом одиночестве! Безо всяких соседей и коэффициентов. Скажем, в уравнениях:
2х+2х+1 = 23 или
2·2х = 24
двойки убирать нельзя!

Вспомним действия со степенями

Пример решения22х - 8х+1 = 0 8 = 23
8х+1 = (23)х+1
(аn)m = anm
8х+1 = (23)х+1 = 23(х+1)
22х - 23(х+1) = 0
22х = 23(х+1)
2х = 3(х+1)
х = -3
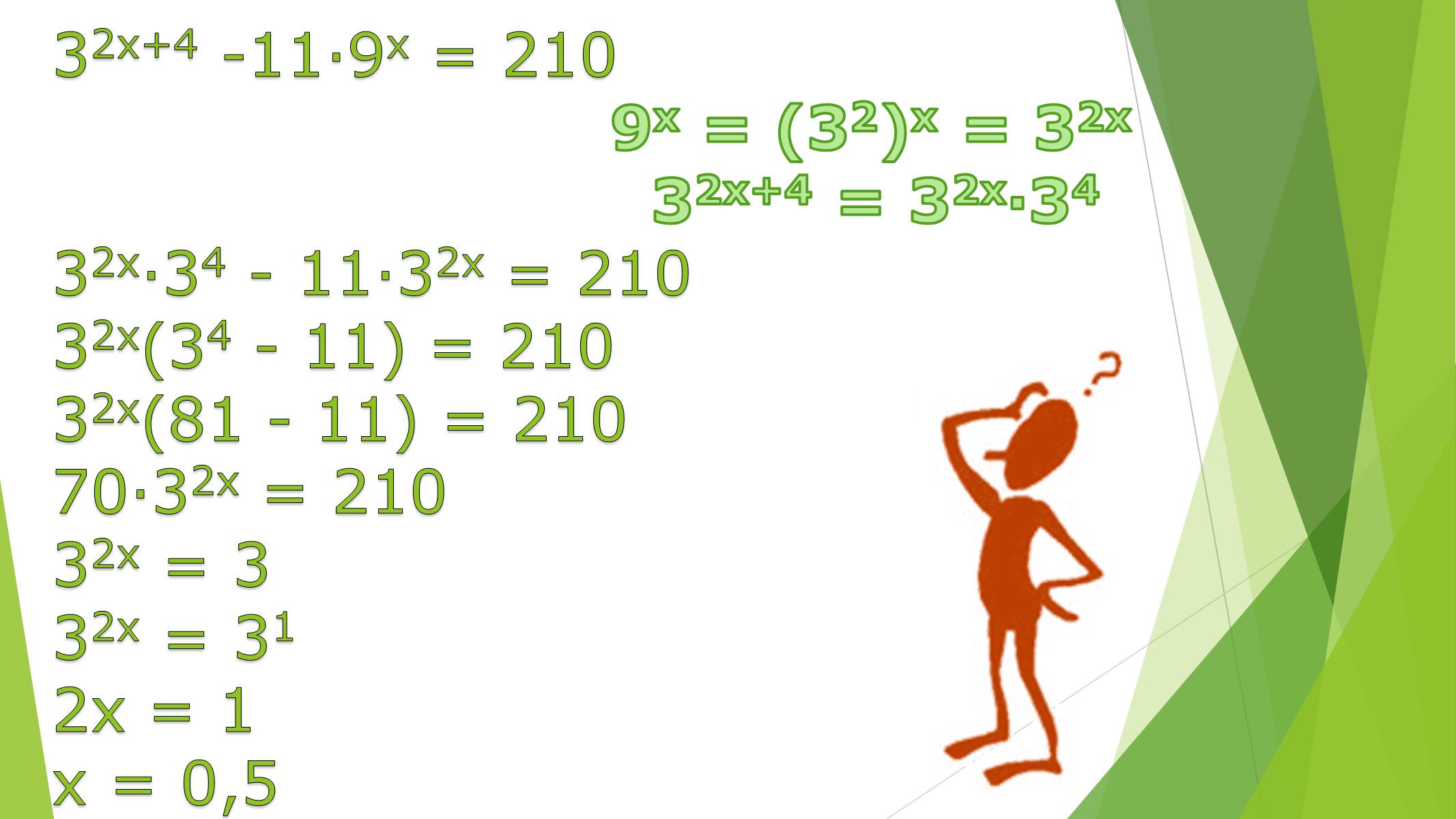
32х+4 -11·9х = 210
9х = (32)х = 32х
32х+4 = 32х·34
32х·34 - 11·32х = 210
32х(34 - 11) = 21032х(81 - 11) = 210
70·32х = 210
32х = 3
32х = 31
2х = 1
х = 0,5

Замена переменной.Биквадратные уравнения
4х - 3·2х +2 = 0 4х = (22)х = 22х
22х - 3·2х +2 = 0
2х = t Тогда 22х = 2х2 = (2х)2 = t2
.t2 - 3t+2 = 0
t1 = 2
t2 = 1.
t1 = 2 = 2х t2 = 1 = 2х
2х = 2 2х = 1
х1 = 1 1 = 20 ( 2х = 20)
х2 = 0

При решении показательных уравнений в конце иногда получается какое-то неудобное выражение. Типа:
2х = 7x = log27

Практические советы:
1. Первым делом смотрим на основания степеней. Соображаем, нельзя ли их сделать одинаковыми. Пробуем это сделать, активно используя действия со степенями. Не забываем, что числа без иксов тоже можно превращать в степени!
2. Пробуем привести показательное уравнение к виду, когда слева и справа стоят одинаковые числа в каких угодно степенях. Используем действия со степенями и разложение на множители. То что можно посчитать в числах - считаем.
3. Если второй совет не сработал, пробуем применить замену переменной. В итоге может получиться уравнение, которое легко решается. Чаще всего - квадратное. Или дробное, которое тоже сводится к квадратному.
4. Для успешного решения показательных уравнений надо степени некоторых чисел знать "в лицо".

Практика

Показательные неравенства

Показательные неравенства

Показательные неравенства

Показательные неравенства

Практика