Презентація на тему «Кути у просторі»

Кути у просторі
Сіденко Віталій
10 клас ГНТН
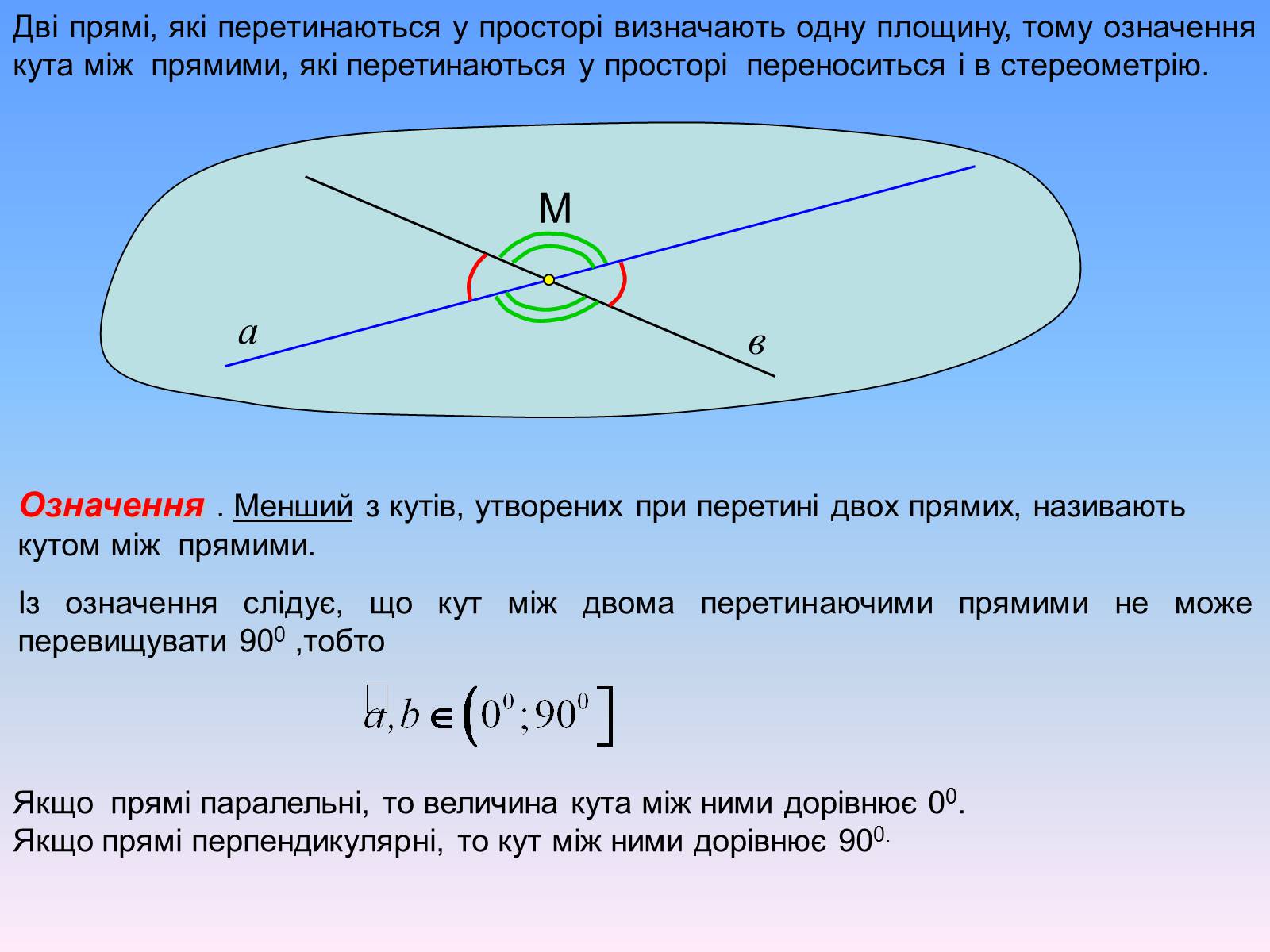
Дві прямі, які перетинаються у просторі визначають одну площину, тому означення кута між прямими, які перетинаються у просторі переноситься і в стереометрію.
а
в
М
Означення . Менший з кутів, утворених при перетині двох прямих, називають кутом між прямими.
Із означення слідує, що кут між двома перетинаючими прямими не може перевищувати 900 ,тобто
Якщо прямі паралельні, то величина кута між ними дорівнює 00.Якщо прямі перпендикулярні, то кут між ними дорівнює 900.
A
B
C
D1
A1
C1
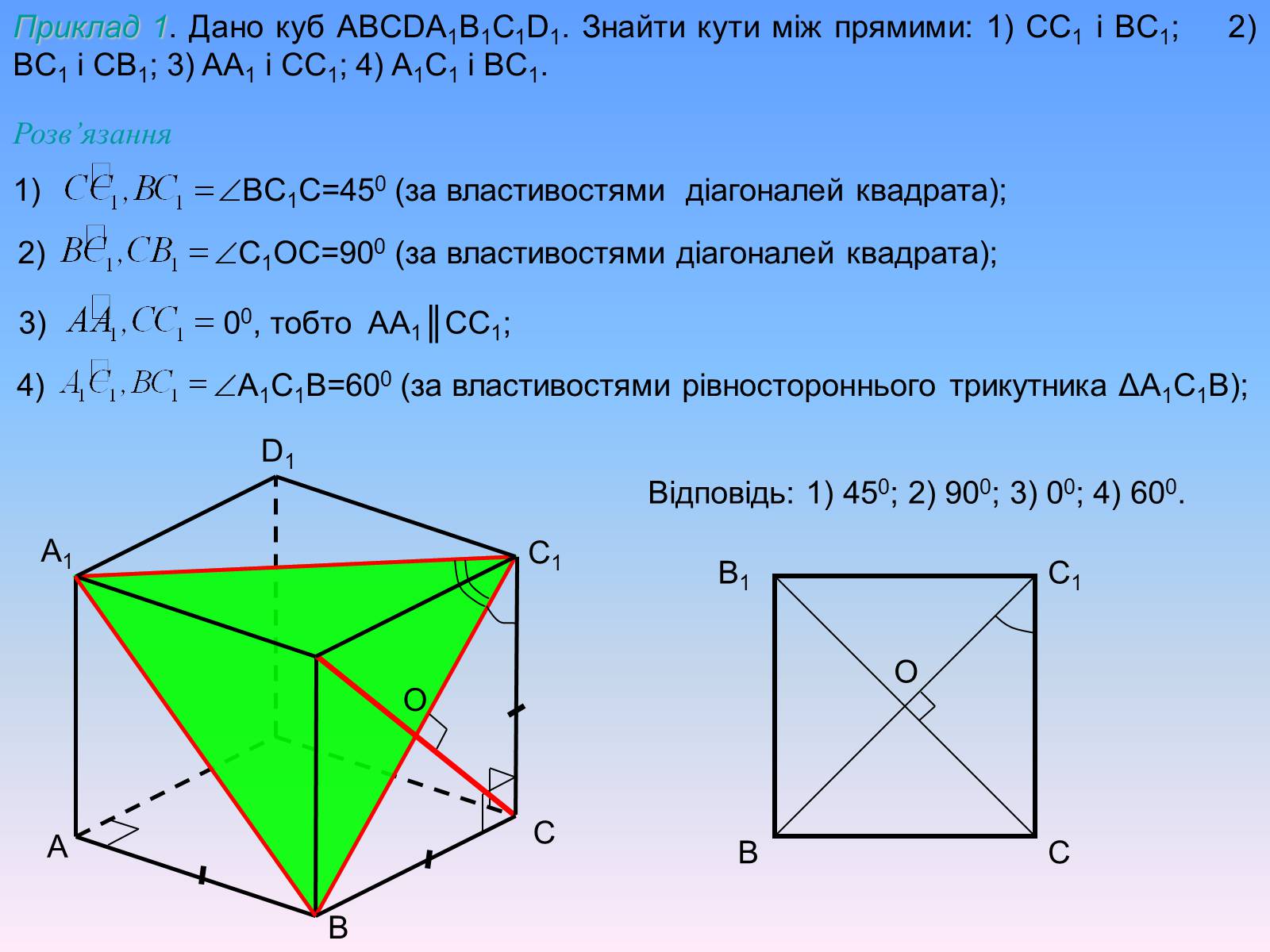
Приклад 1. Дано куб ABCDA1B1C1D1. Знайти кути між прямими: 1) CC1 і BC1; 2) BC1 і CB1; 3) AA1 і CC1; 4) A1C1 і BC1.
B
C
C1
В1
Розв'язання
1) BC1C=450 (за властивостями діагоналей квадрата);
2) C1ОC=900 (за властивостями діагоналей квадрата);
О
О
3) 00, тобто AA1║CC1;
4) A1C1B=600 (за властивостями рівностороннього трикутника ΔA1C1B);
Відповідь: 1) 450; 2) 900; 3) 00; 4) 600.
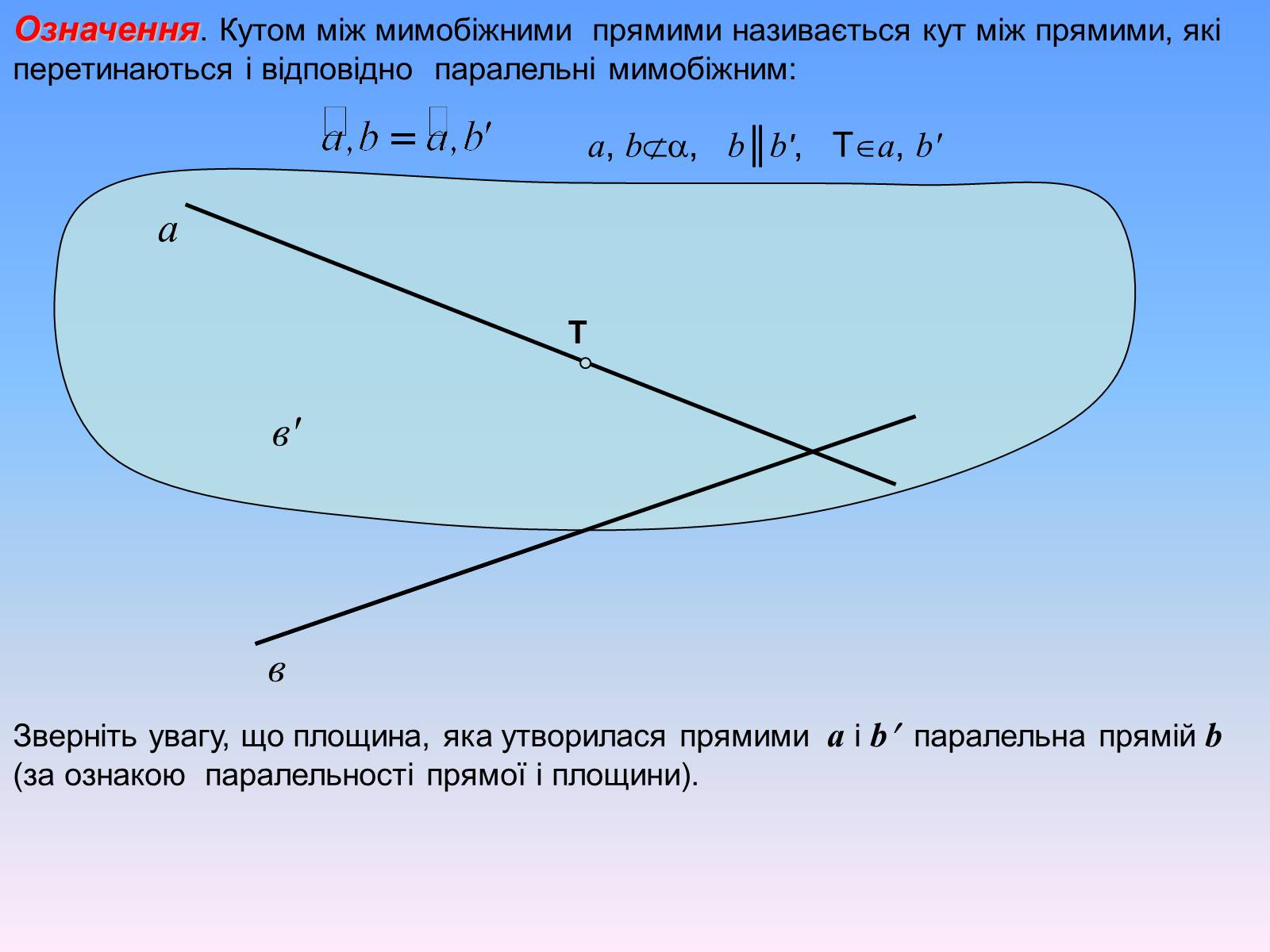
Означення. Кутом між мимобіжними прямими називається кут між прямими, які перетинаються і відповідно паралельні мимобіжним:
а
в
в'
T
a, b, b║b', Ta, b'
Зверніть увагу, що площина, яка утворилася прямими a і b паралельна прямій b (за ознакою паралельності прямої і площини).
A
B
C
D1
A1
C1
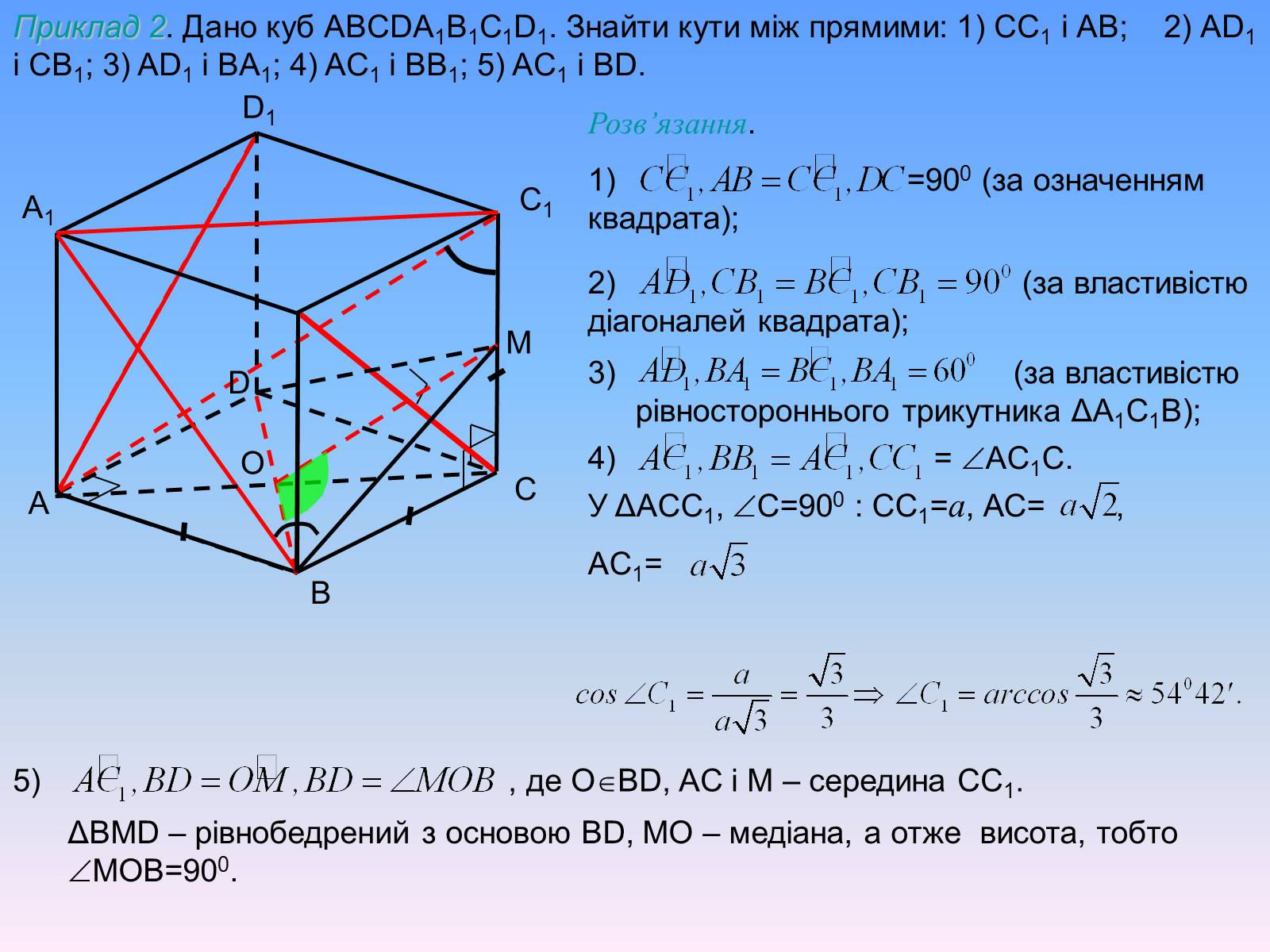
Приклад 2. Дано куб ABCDA1B1C1D1. Знайти кути між прямими: 1) CC1 і АB; 2) AD1 і CB1; 3) AD1 і BA1; 4) AC1 і BB1; 5) AC1 і BD.
Розв'язання.
1) =900 (за означенням квадрата);
2) (за властивістю діагоналей квадрата);
3) (за властивістю рівностороннього трикутника ΔA1C1B);
4) = AC1С.
У ΔACC1, С=900 : СС1=а, АС= ,
AC1=
5) , де ОBD, AC і М – середина СС1.
O
M
ΔBMD – рівнобедрений з основою BD, МО – медіана, а отже висота, тобто MOB=900.
D
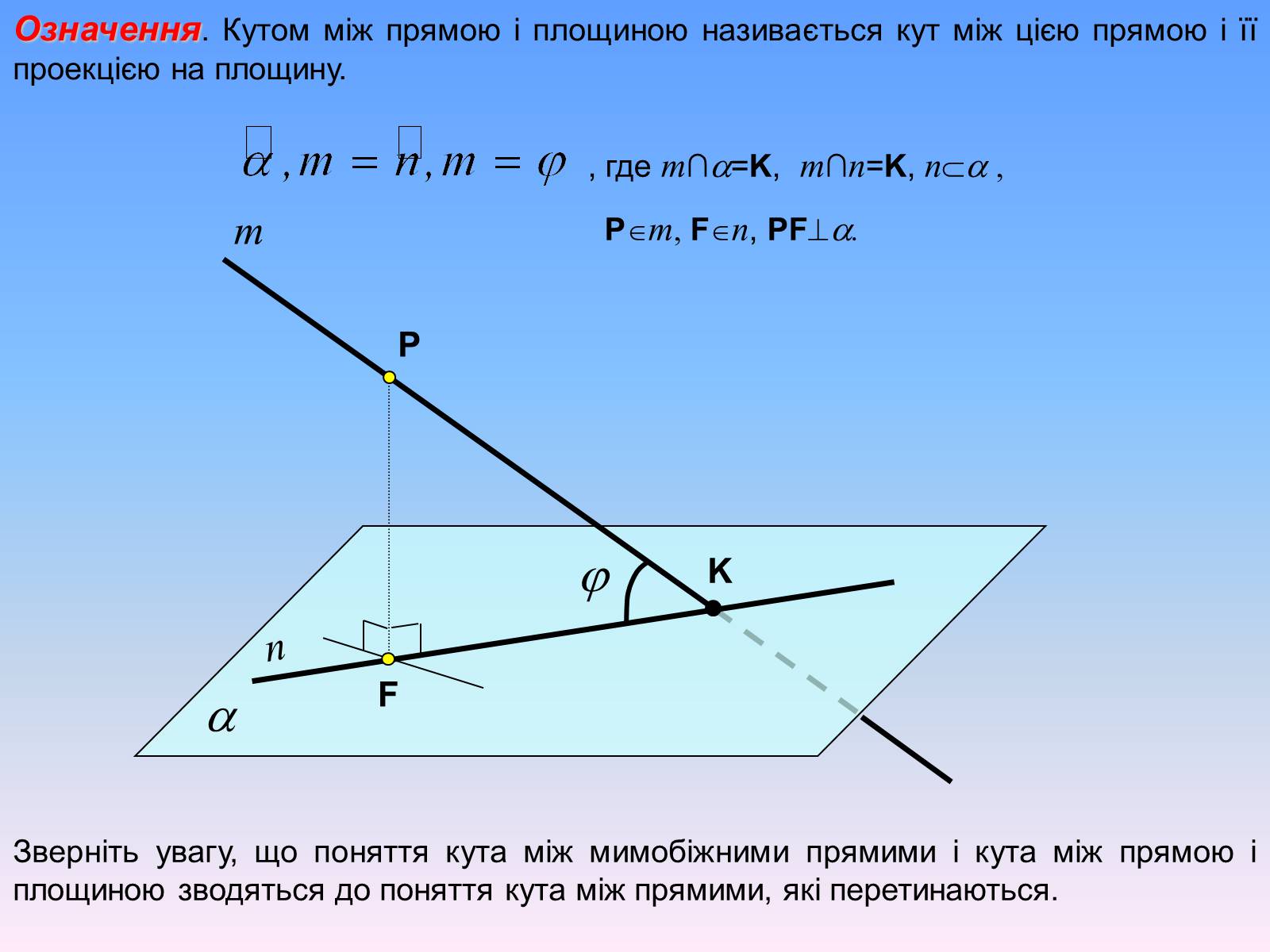
Означення. Кутом між прямою і площиною називається кут між цією прямою і її проекцією на площину.
т
n
K
, где m∩=K, m∩n=K, n ,
Pm, Fn, PF.
P
F
Зверніть увагу, що поняття кута між мимобіжними прямими і кута між прямою і площиною зводяться до поняття кута між прямими, які перетинаються.
A
C
D1
A1
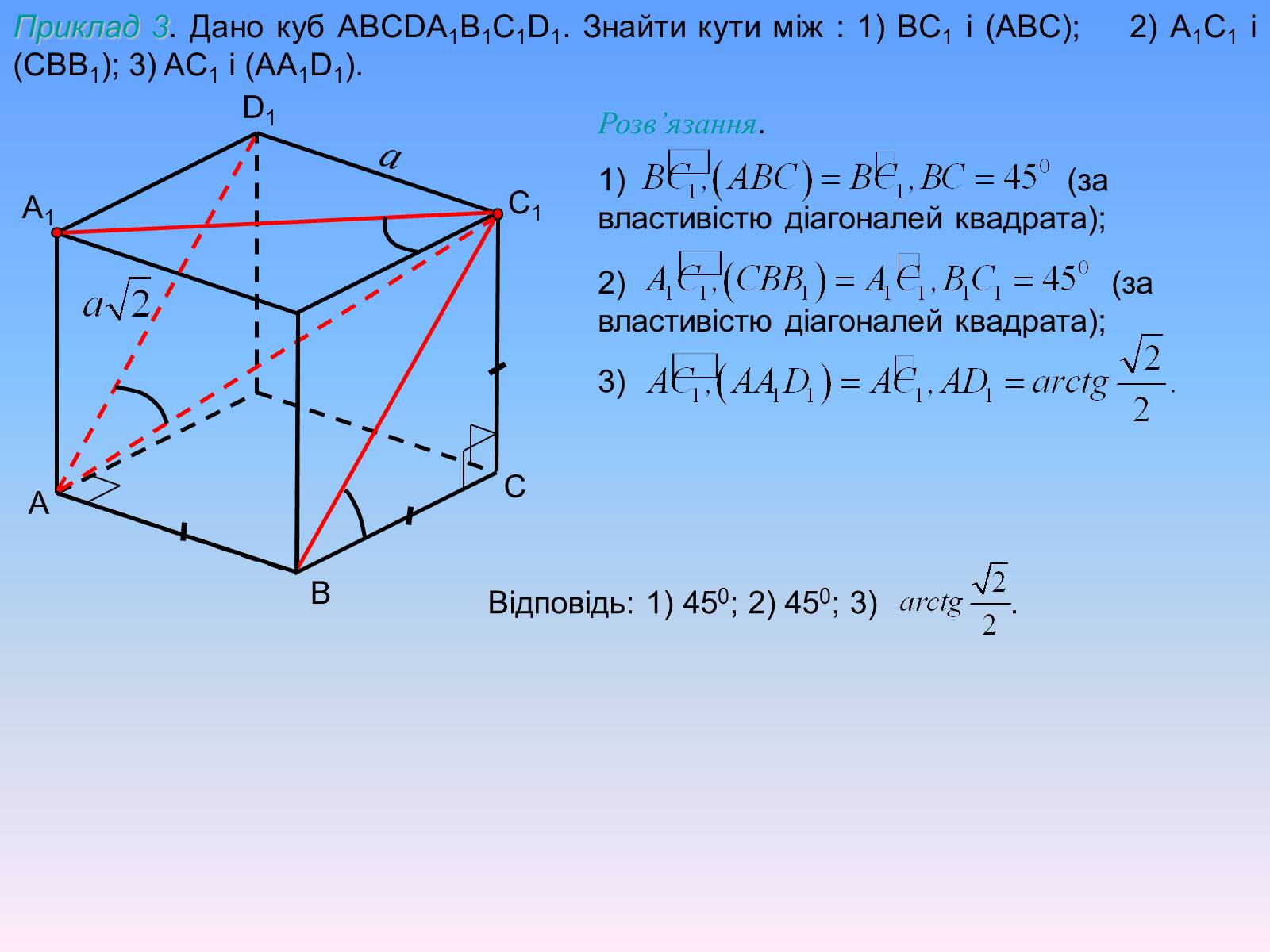
Приклад 3. Дано куб ABCDA1B1C1D1. Знайти кути між : 1) BC1 і (АBC); 2) A1C1 і (CBB1); 3) AC1 і (AA1D1).
B
C1
Розв'язання.
1) (за властивістю діагоналей квадрата);
2) (за властивістю діагоналей квадрата);
3)
a
Відповідь: 1) 450; 2) 450; 3) .