Презентація на тему «Бісектор двогранного кута»

Проект на тему:
“Бісектор двогранного кута”

Бісектор двогранного кута
Бісектором двогранного кута називають півплощину, що поділяє його на два рівні двогранних кути. Границею бісектора є ребро двогранного кута.

Бісектор існує для будь-якого двограноого кута
Будуємо бісектор двогранного кута
1) будуємо лінійний кут АОВ даного двогранного кута αnβ
2) у (АОВ) будуємо бісектрису l кута АОВ
Півплощина, що визначена ребром даного кута n і променем l, є шуканим бісектором кута αnβ
Площина АОВ перпендикулярна до спільного ребра n даного й утворених двогранних кутів. Тоді кути АОВ, АОС, СОВ-лінійні кути двогранних кутів αn β, αnγ, γnβ відповідно. За побудовою промінь l – бісектриса кута АОВ, тобто ∠АОС= ∠СОВ. Тоді двогранні кути αnγ і γnβ рівні, γ- бісектор αnβ.
А
а
n
b
C
B
β
γ
l
α
O
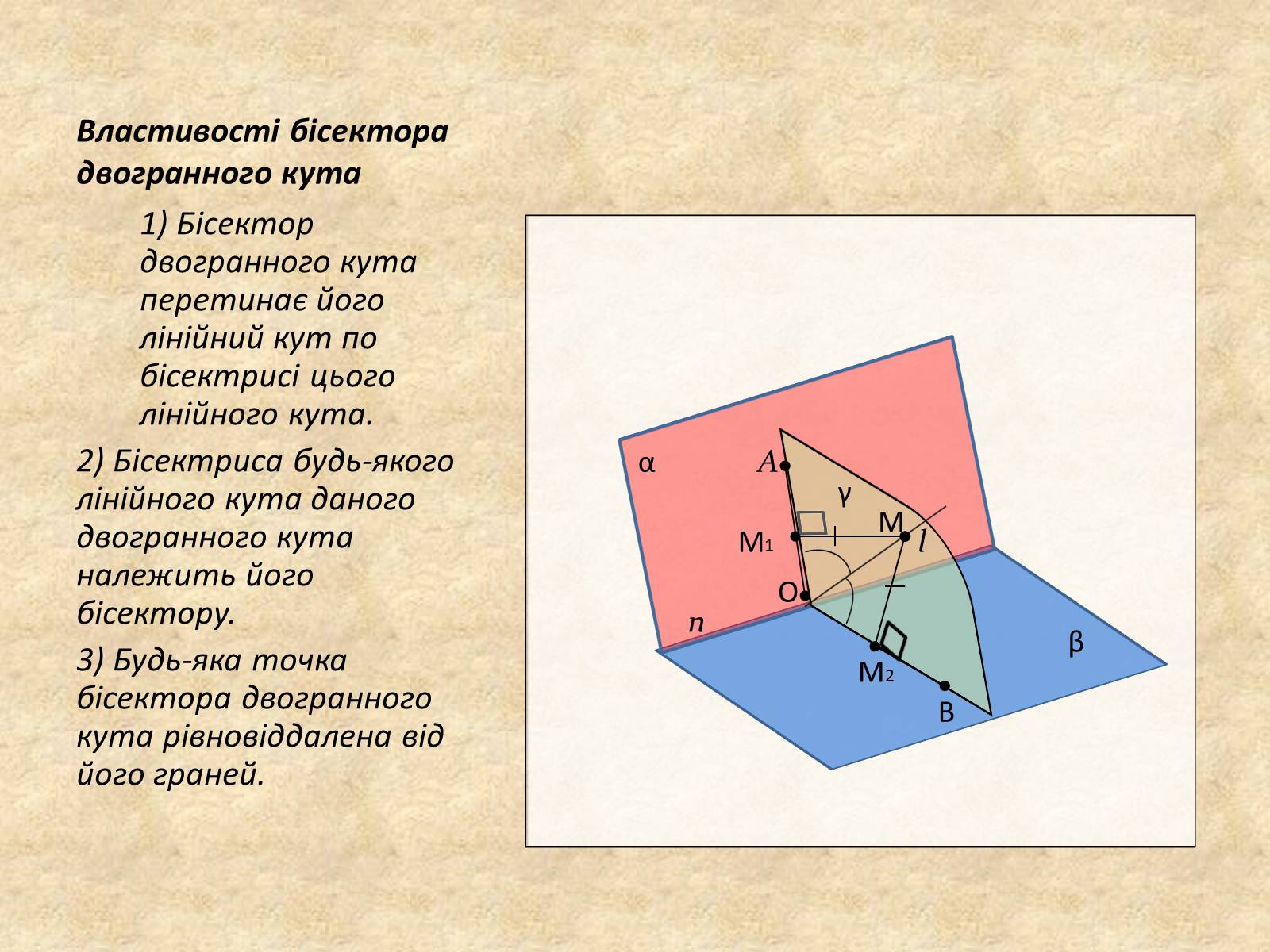
Властивості бісектора двогранного кута
1) Бісектор двогранного кута перетинає його лінійний кут по бісектрисі цього лінійного кута.
2) Бісектриса будь-якого лінійного кута даного двогранного кута належить його бісектору.
3) Будь-яка точка бісектора двогранного кута рівновіддалена від його граней.
α
А
γ
М
М1
l
О
М2
В
n
β
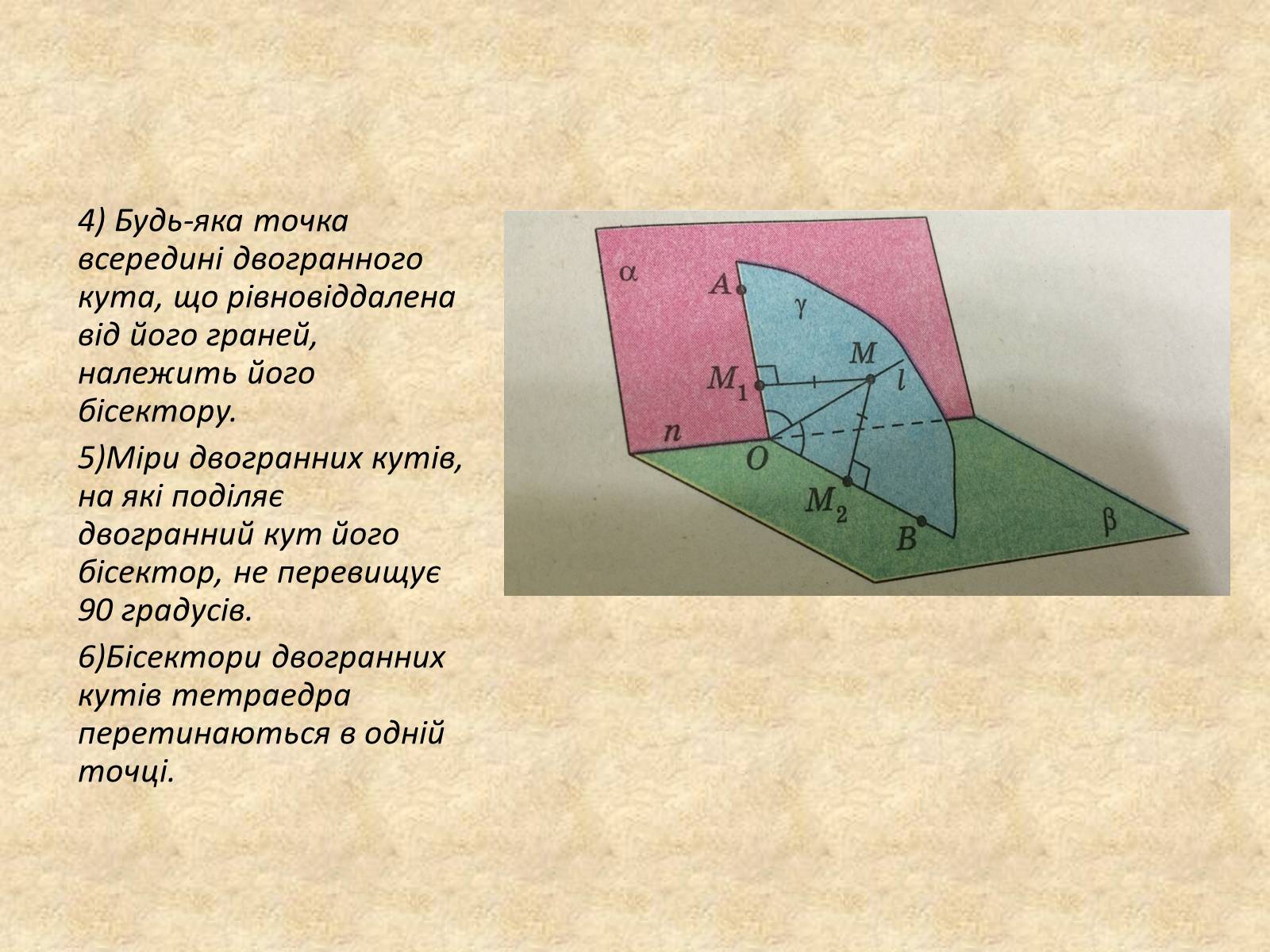
4) Будь-яка точка всередині двогранного кута, що рівновіддалена від його граней, належить його бісектору.
5)Міри двогранних кутів, на які поділяє двогранний кут його бісектор, не перевищує 90 градусів.
6)Бісектори двогранних кутів тетраедра перетинаються в одній точці.

Роботу виконали учні 11-А класу: Кальницький Денис та Стабровська Ганна