Презентація на тему «Похідна» (варіант 2)

Похідна
Геометричний та фізичний зміст похідної
х
у
о
y = (x)
х0
х0 + х
х
у
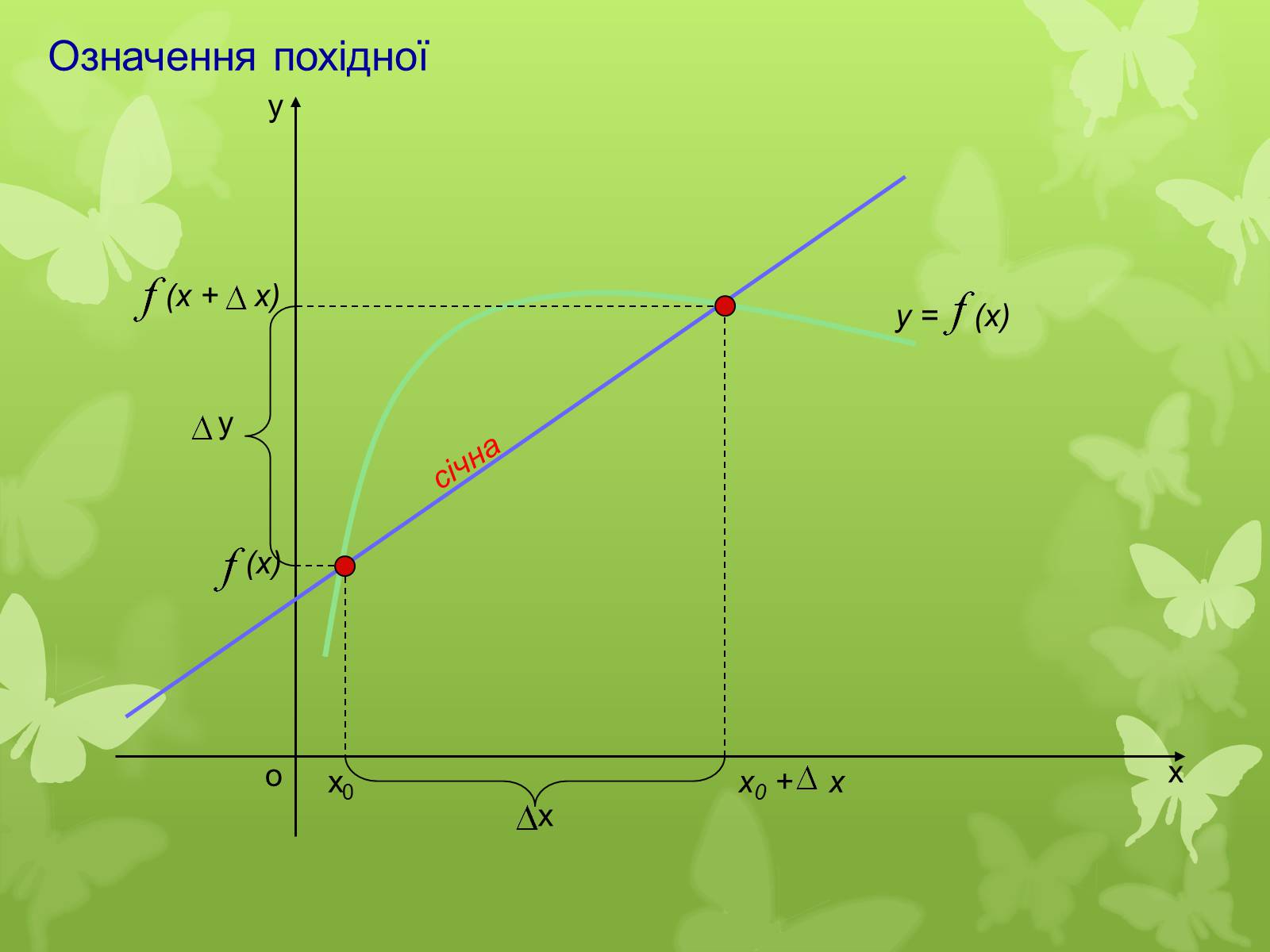
(х + х)
(х)
Означення похідної
січна
х
у
о
y = (x)
х0
у0
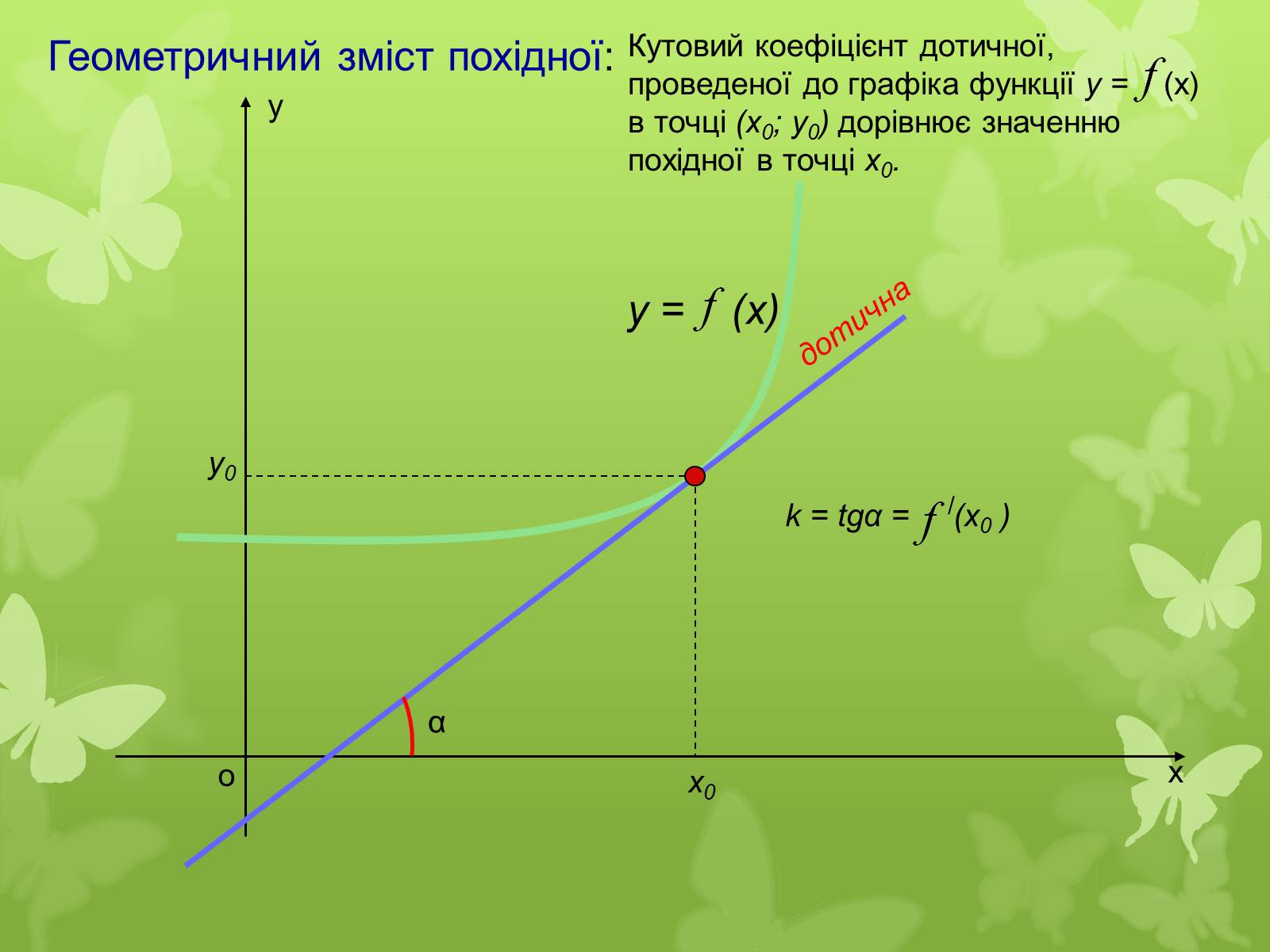
Геометричний зміст похідної:
k = tgα = (x0 )
α
Кутовий коефіцієнт дотичної,
проведеної до графіка функції у = (x)
в точці (х0; у0) дорівнює значенню
похідної в точці х0.
/
дотична

Геометричний зміст похідної:
Кутовий коефіцієнт дотичної,
проведеної до графіка функції у = f (x)
в точці (х0 ; у0) дорівнює значенню
похідної в точці х0.
k – кутовий коефіцієнт дотичної
k = tg α, α – кут нахилу дотичної
k = (x0)
/
х
у
о
y = (x)
х0
у0
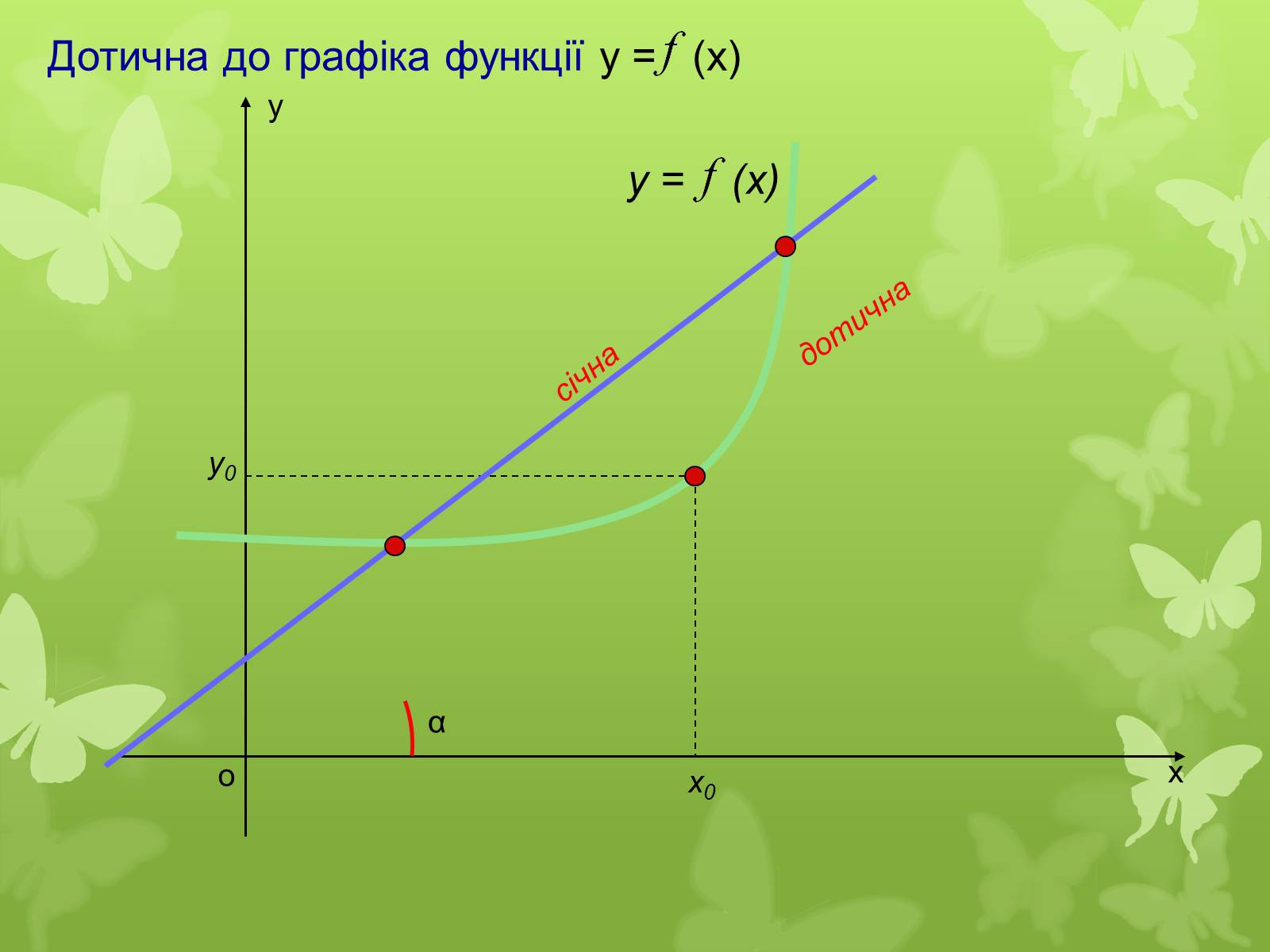
Дотична до графіка функції у = (х)
α
січна
дотична
х
у
о
y = (x)
х0
у0
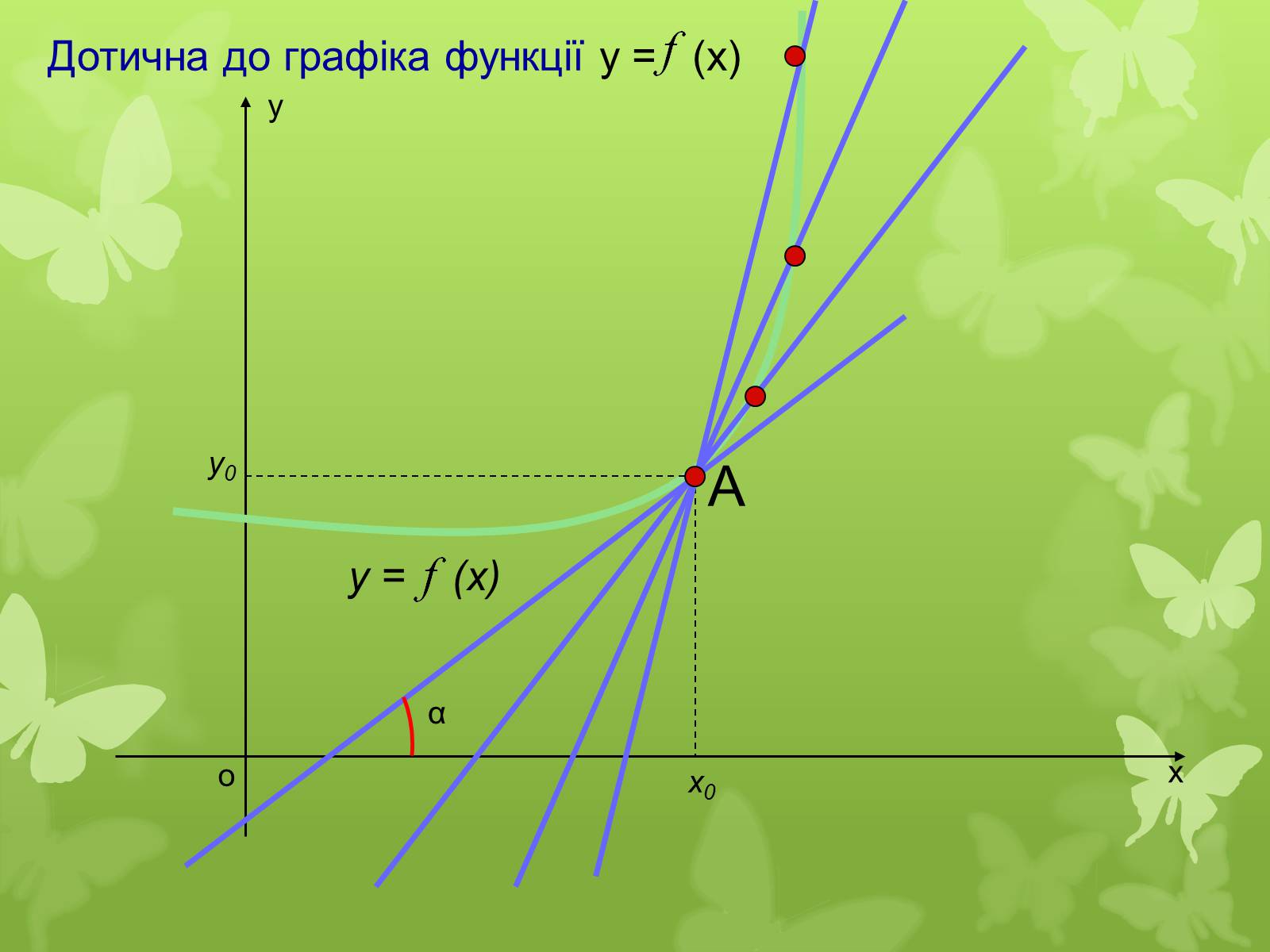
Дотична до графіка функції у = (х)
α
А
х
у
о
y = (x)
х0
у0
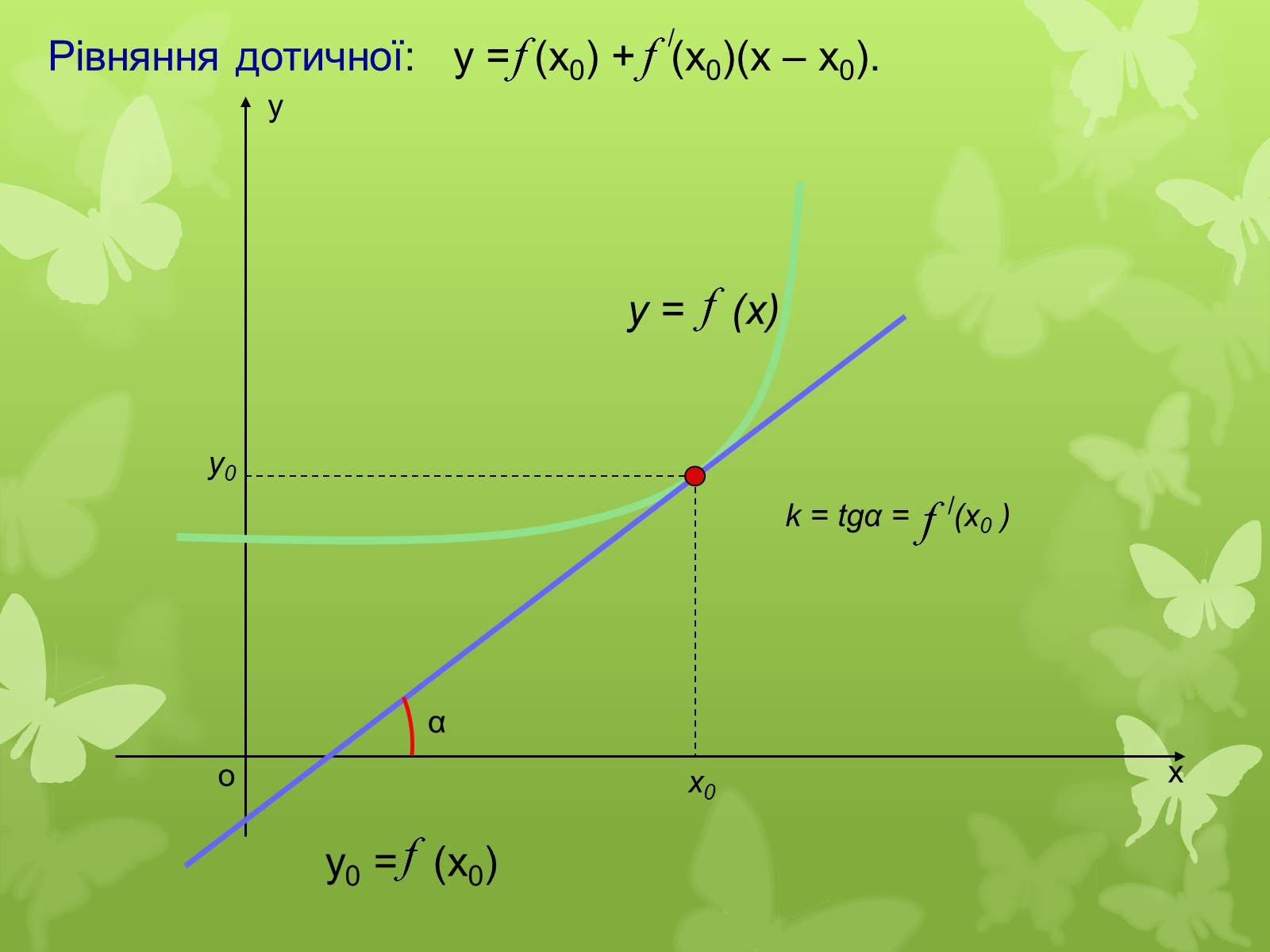
Рівняння дотичної: у = (х0) + (х0)(х – х0).
k = tgα = (x0 )
α
/
/
у0 = (х0)

Механічний зміст похідної:
х0 – координата точки
v(t0)- швидкість точки в момент
часу t0
а(t0) – прискорення точки
в момент часу t0
/
v(t0) = x (t0)
/
a(t0) = v (t0)

Похідна
Застосування похідної
х
у
о
y = (x)
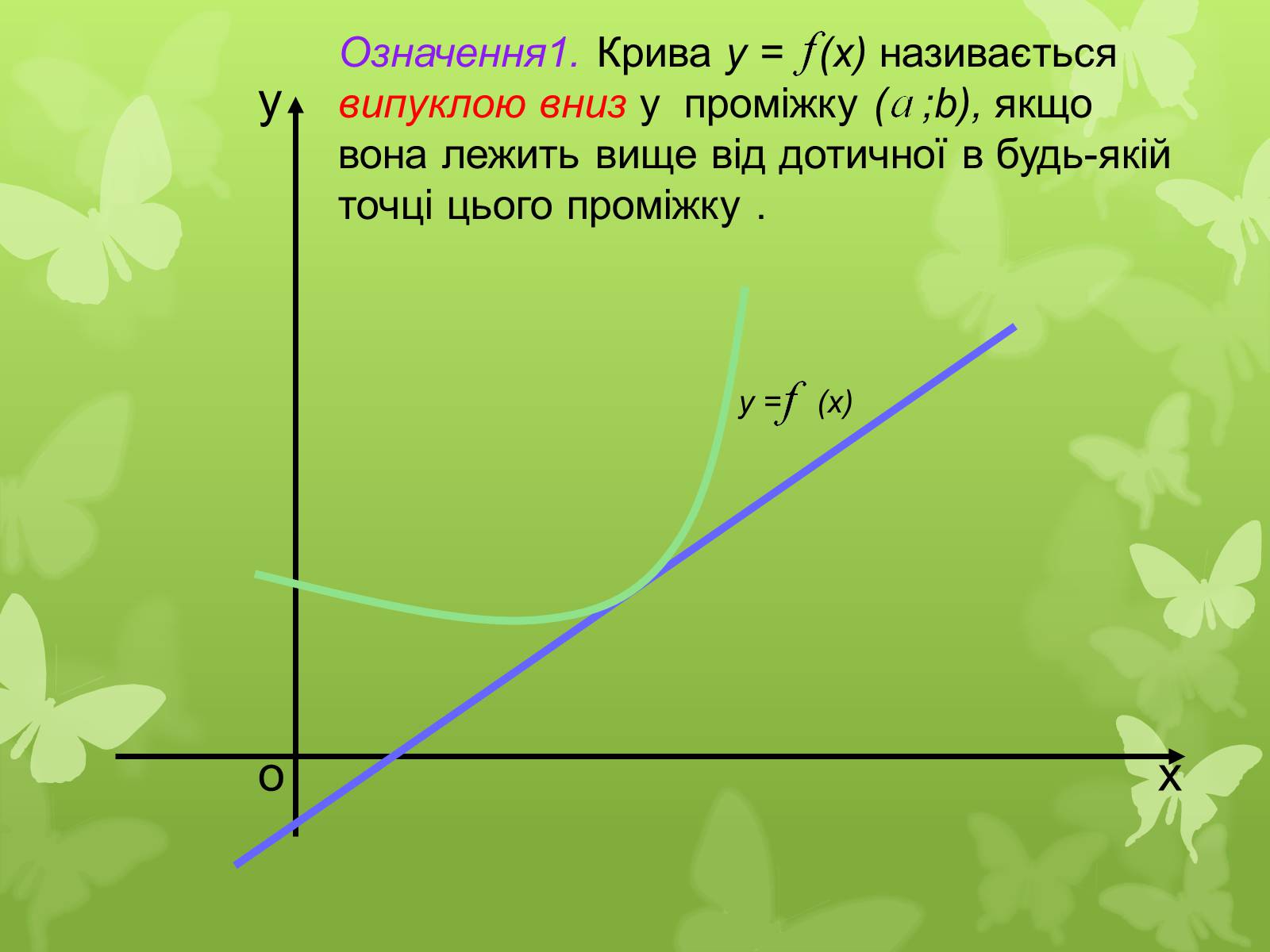
Означення1. Крива у = (x) називається випуклою вниз у проміжку ( ;b), якщо вона лежить вище від дотичної в будь-якій точці цього проміжку .
х
у
о
y = (x)
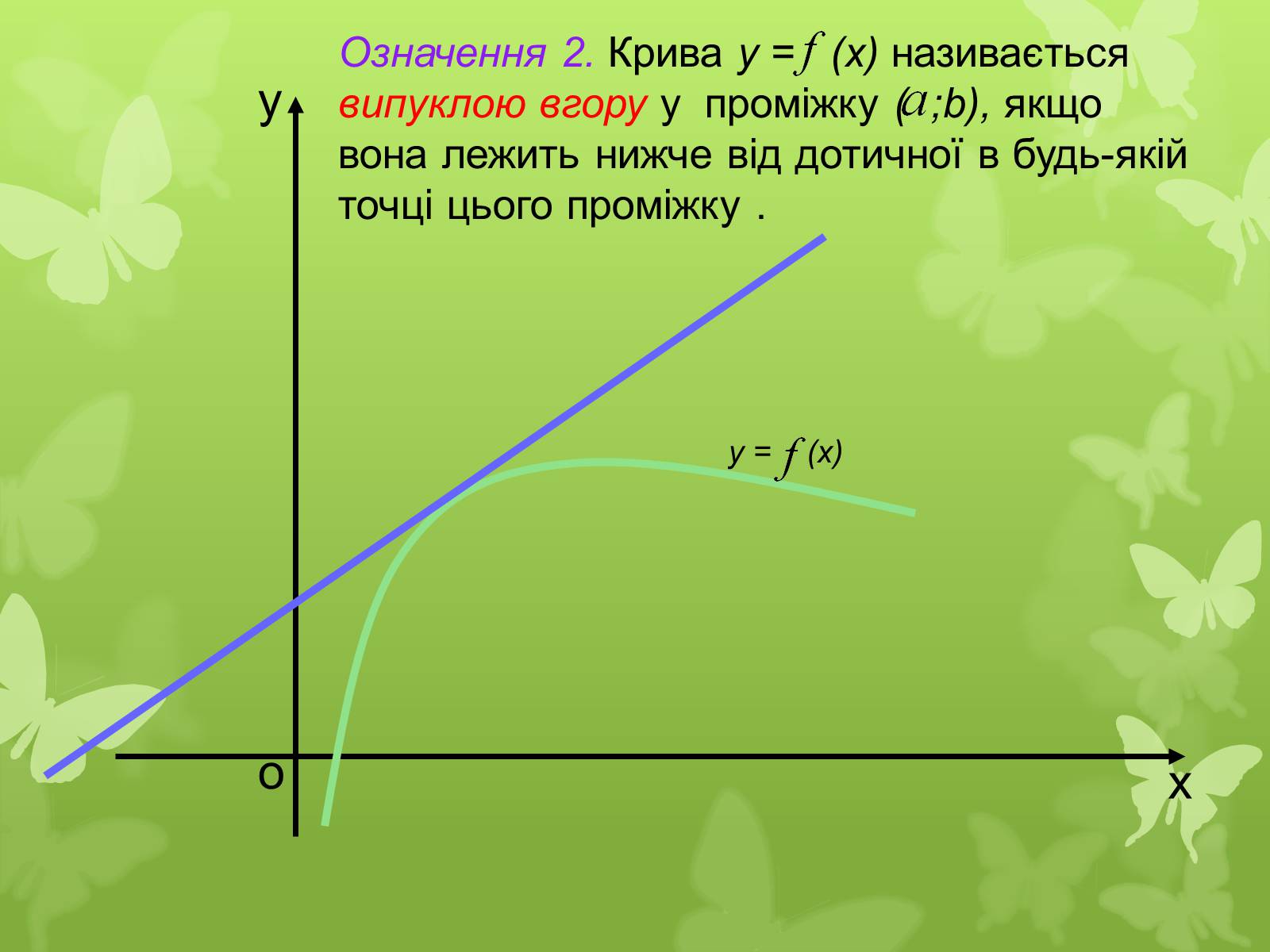
Означення 2. Крива у = (x) називається випуклою вгору у проміжку ( ;b), якщо вона лежить нижче від дотичної в будь-якій точці цього проміжку .
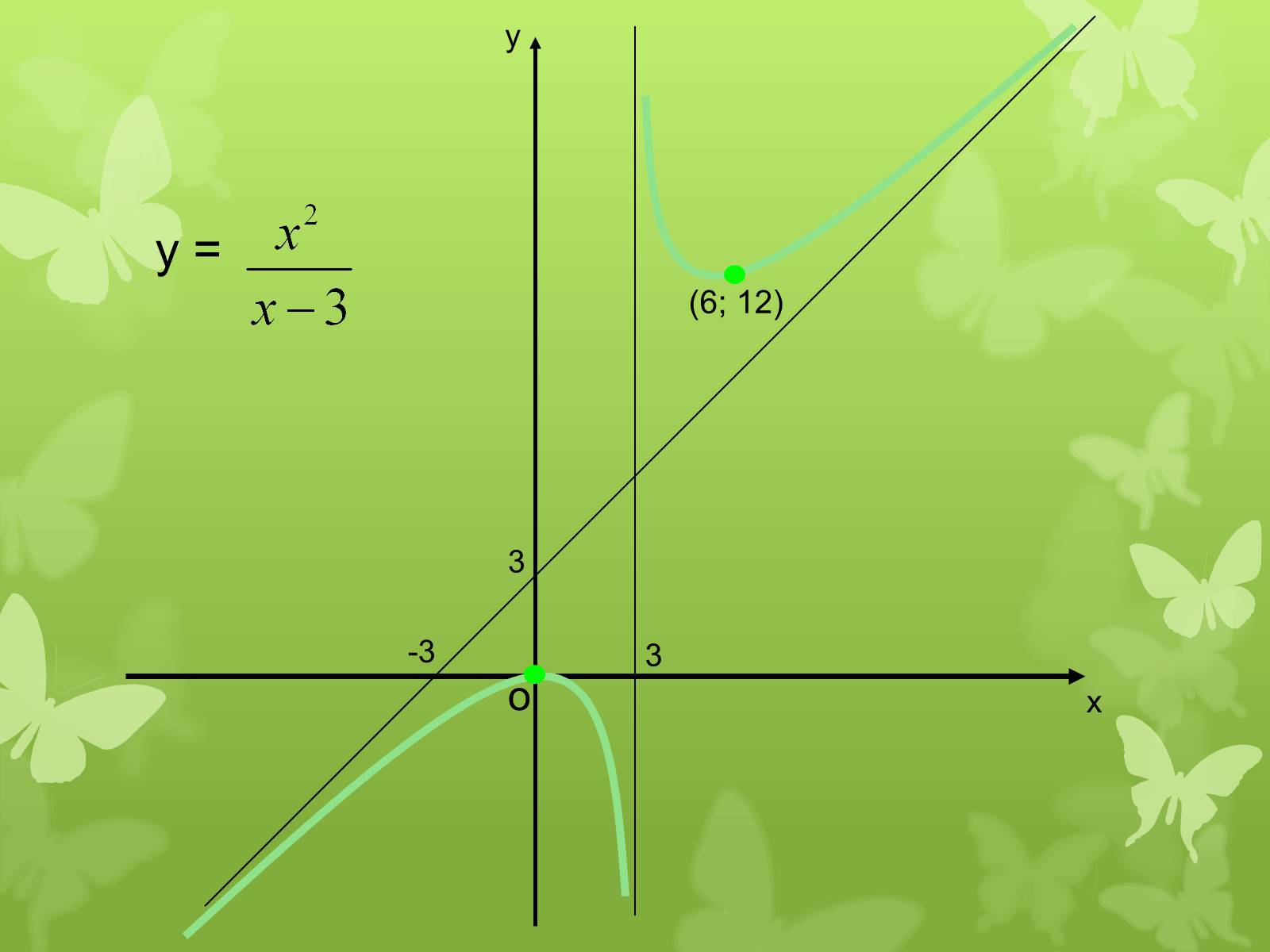
у
х
о
-3
3
3
у =
(6; 12)