Презентація на тему «Параллельность прямых и плоскостей в пространстве»

Параллельность прямых и плоскостей в пространстве.
Выполнила
ученица 10 класса
Нетребко Галина
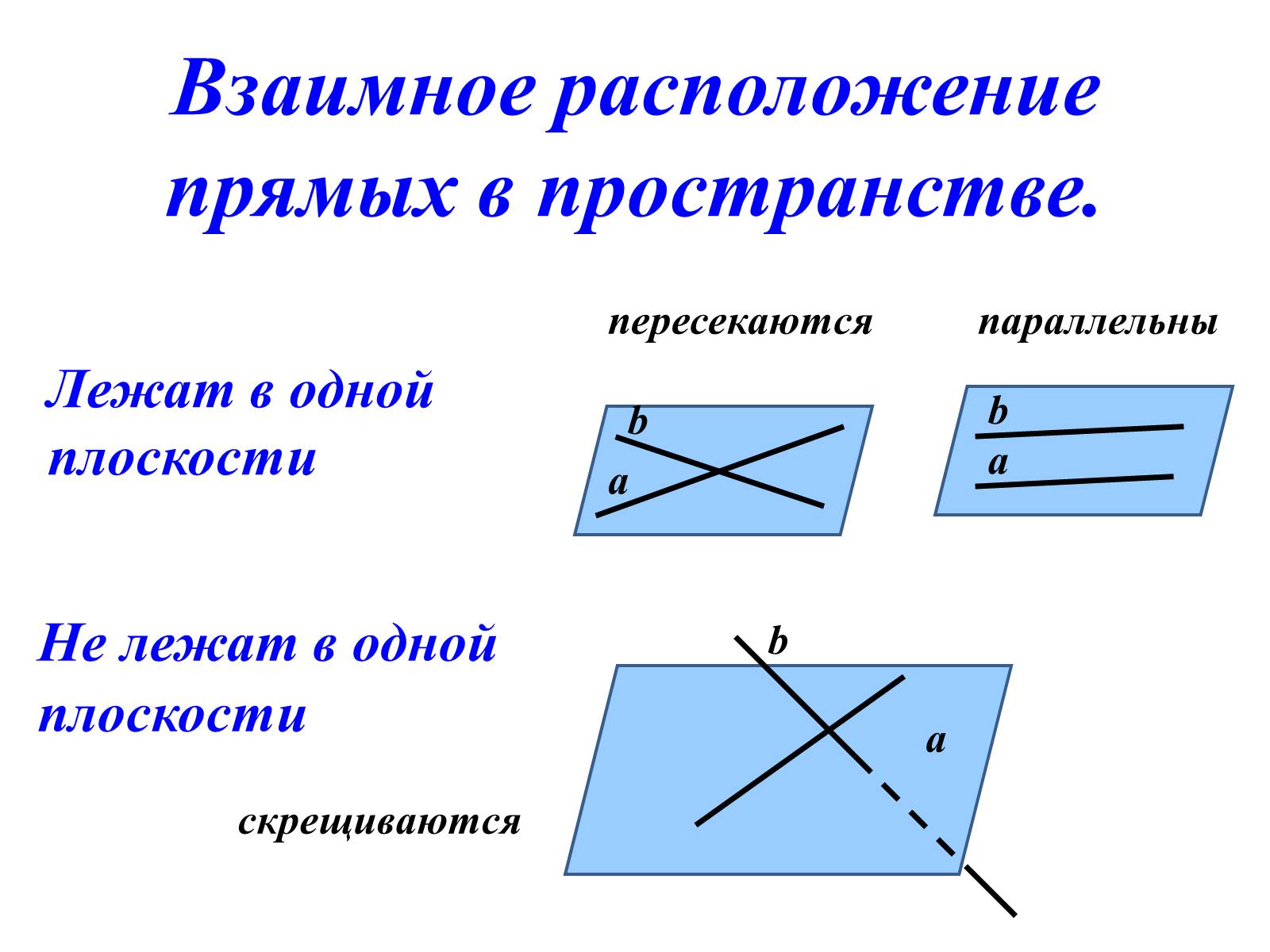
пересекаются
параллельны
а
а
а
b
b
b
скрещиваются
Лежат в одной плоскости
Не лежат в одной плоскости
Взаимное расположение прямых в пространстве.
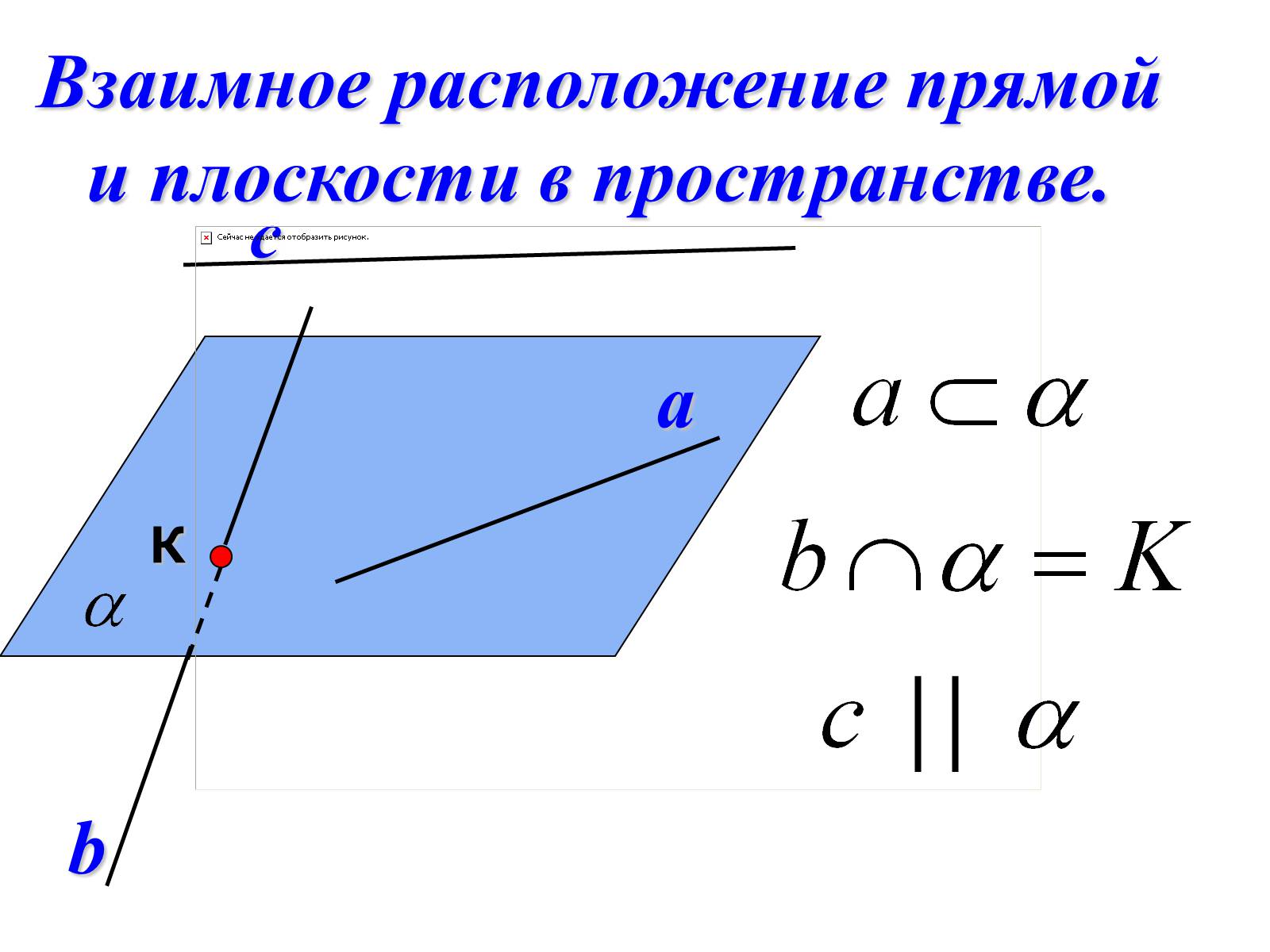
a
с
Взаимное расположение прямой и плоскости в пространстве.
b
К
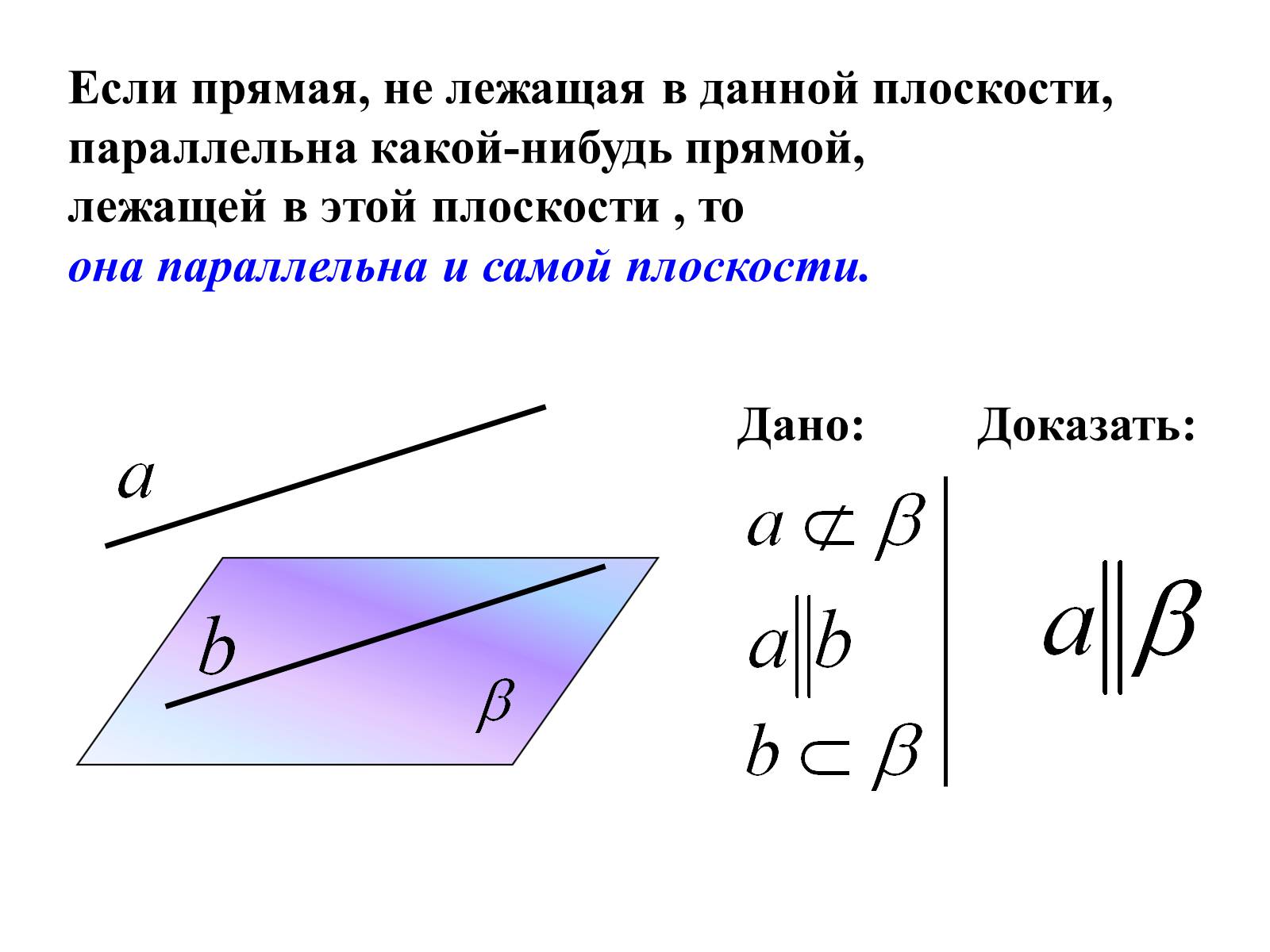
Если прямая, не лежащая в данной плоскости,
параллельна какой-нибудь прямой,
лежащей в этой плоскости , то
она параллельна и самой плоскости.
Дано:
Доказать:

1.Через прямые a и b проведем плоскость α
Пусть , ,
α
2. α β = b
Если a β = Х, то Х b, это невозможно, т.к. α b
a β
a β
Теорема доказана.
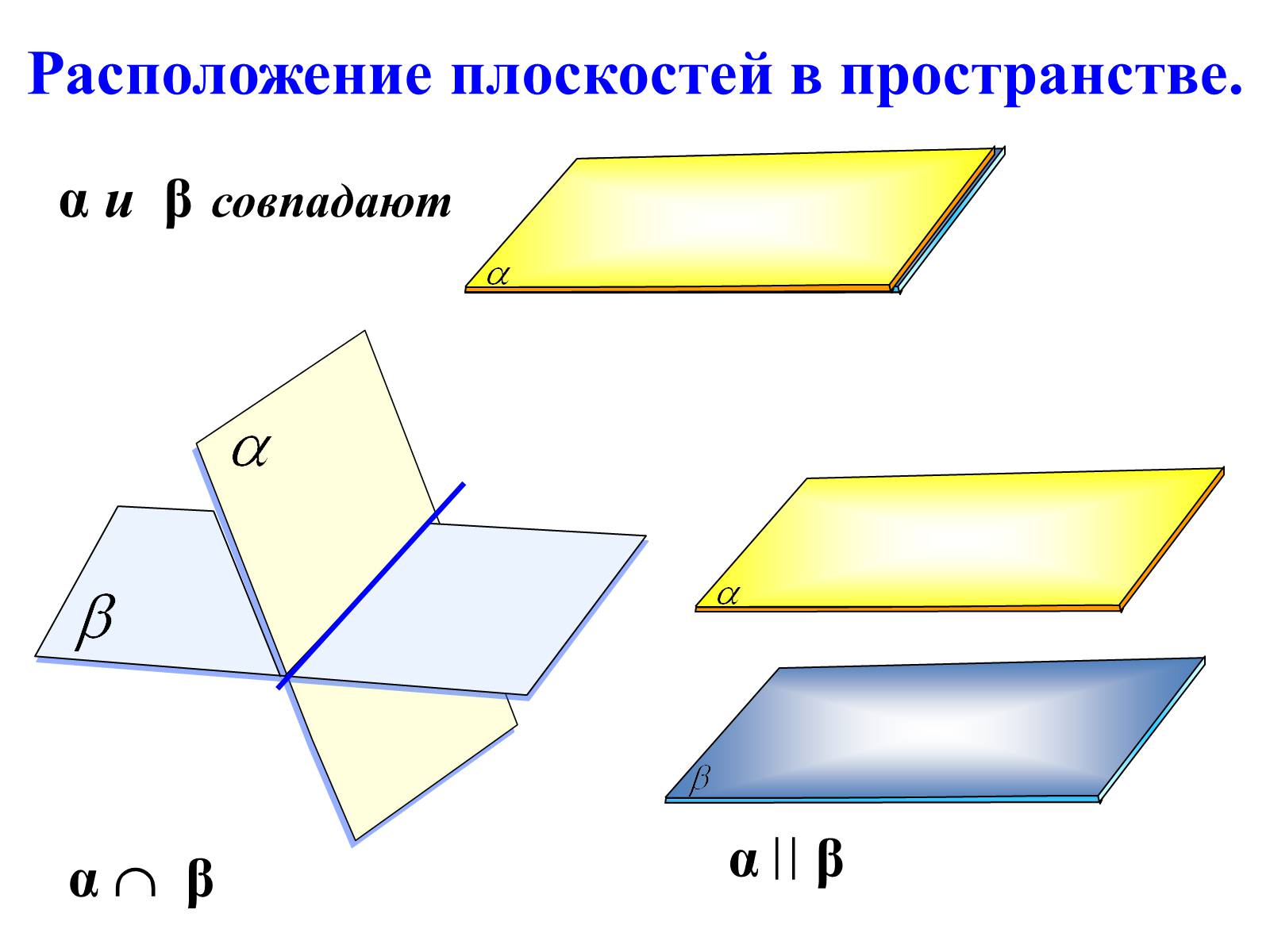
Расположение плоскостей в пространстве.
α β
α и β совпадают
α β

Признак параллельности двух плоскостей.
Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум
пересекающимся прямым другой плоскости, то эти
плоскости параллельны.
Дано: а b = M, a , b .
a₁ b₁, a₁ , b₁ . a a₁, b b₁.
Доказать:
а
а₁
b
b₁
M
c
Доказательство:
Тогда а , а , = с, значит а с.
2. b , b , = с, значит b с.
3. Имеем, что через точку М проходят две прямые а и b, параллельные прямой с, чего быть на может.
Значит .
1. Пусть = с.
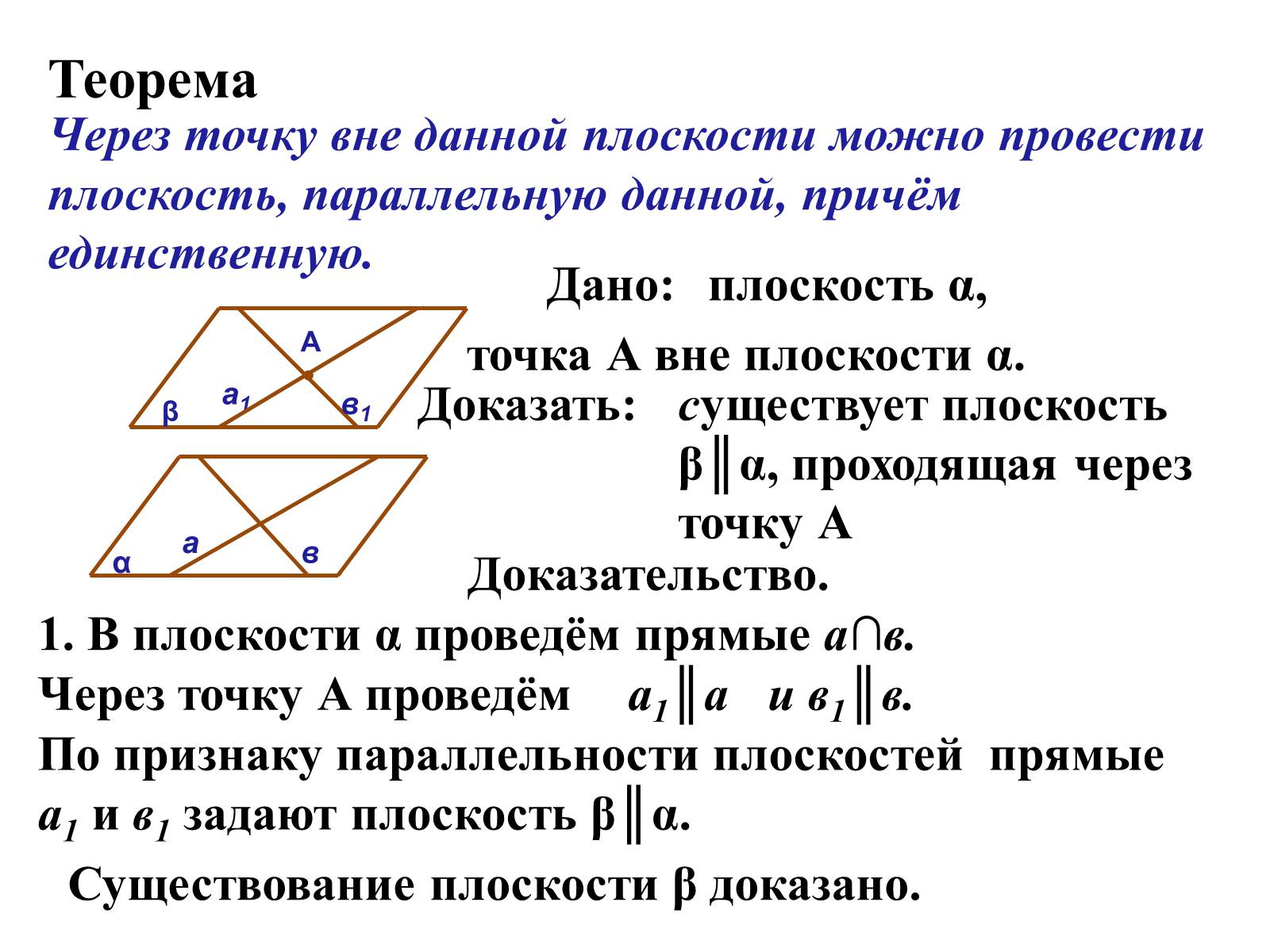
Теорема
Через точку вне данной плоскости можно провести плоскость, параллельную данной, причём единственную.
β
а1
•
А
α
плоскость α,
в1
в
а
Доказать:
Доказательство.
Дано:
точка А вне плоскости α.
существует плоскость β║α, проходящая через точку А
1. В плоскости α проведём прямые а∩в.
Через точку А проведём
а1║а
и в1║в.
По признаку параллельности плоскостей прямые а1 и в1 задают плоскость β║α.
Существование плоскости β доказано.

а
b
Если две параллельные плоскости
пересечены третьей, то линии их пересечения параллельны.
Свойство параллельных плоскостей.
Дано:
α β, α = a
β = b
Доказать: a b
Доказательство:
1. a , b
2. Пусть a b,
тогда a b = М
3. M α, M β
α β = с (А2)
Получили противоречие с условием.
Значит a b ч. т.д.
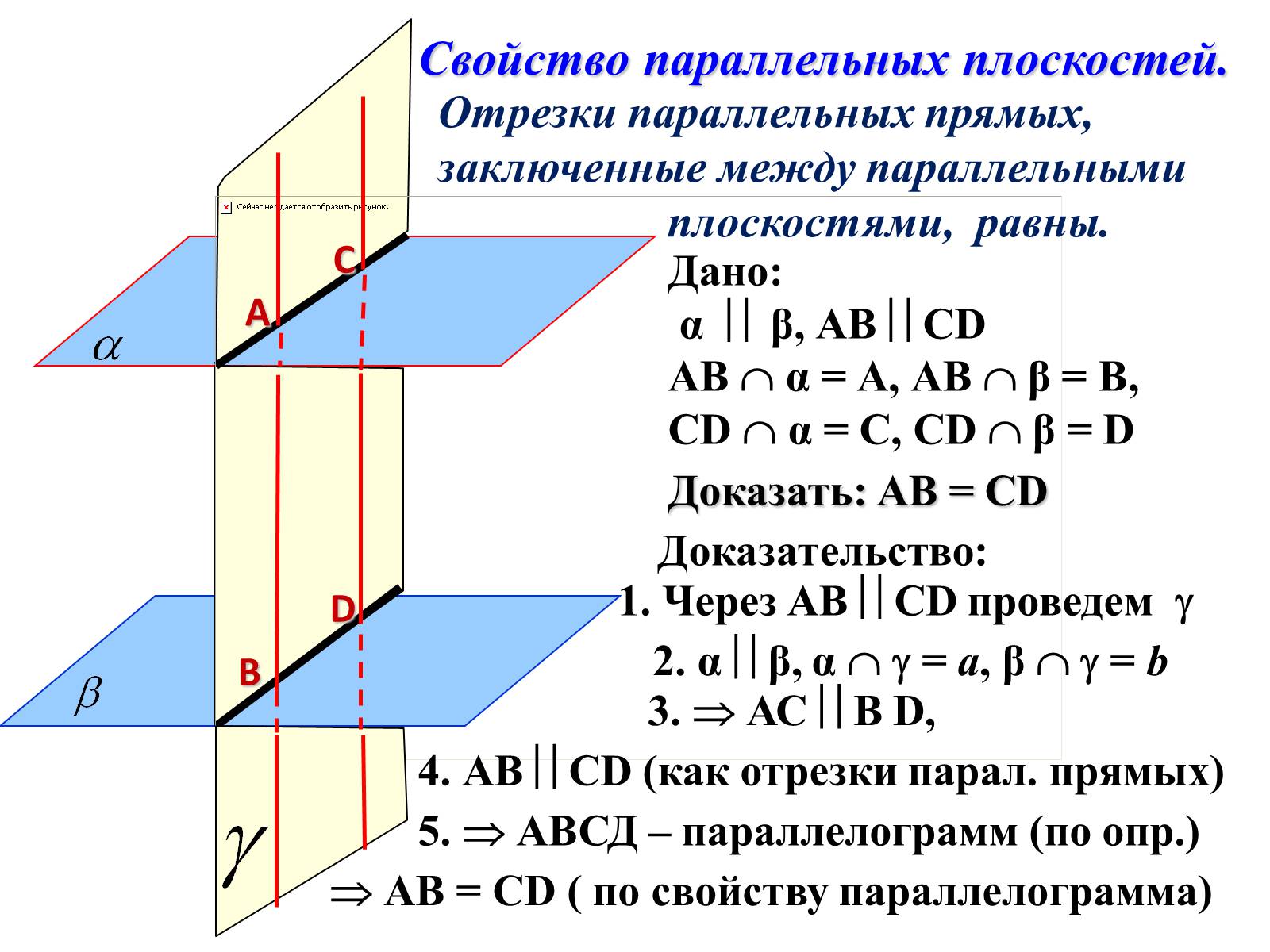
Отрезки параллельных прямых,
заключенные между параллельными
плоскостями, равны.
Свойство параллельных плоскостей.
А
В
С
D
Доказать: АВ = СD
Дано:
α β, АВ СD
АВ α = А, АВ β = В,
СD α = С, СD β = D
Доказательство:
1. Через АВ СD проведем
2. α β, α = a, β = b
3. АС В D,
4. АВ СD (как отрезки парал. прямых)
5. АВСД – параллелограмм (по опр.)
АВ = СD ( по свойству параллелограмма)
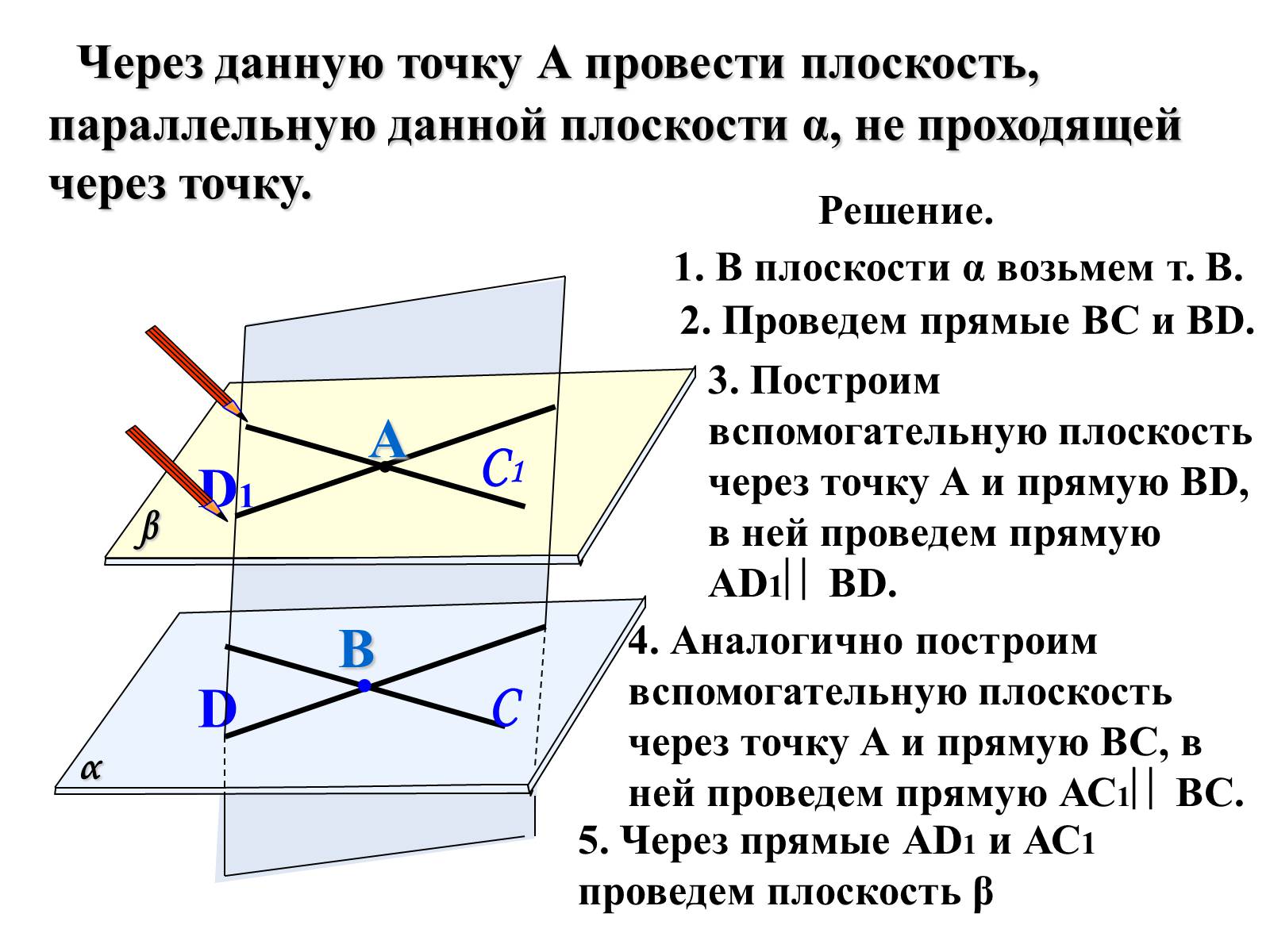
Через данную точку А провести плоскость, параллельную данной плоскости α, не проходящей через точку.
α
β
А
Решение.
1. В плоскости α возьмем т. В.
2. Проведем прямые ВС и ВD.
В
•
С1
D1
D
С
3. Построим вспомогательную плоскость через точку А и прямую ВD, в ней проведем прямую АD1 ВD.
4. Аналогично построим вспомогательную плоскость через точку А и прямую ВС, в ней проведем прямую АС1 ВС.
•
5. Через прямые АD1 и АС1 проведем плоскость β