Презентація на тему «Штучний інтелект та евристичний алгоритм А*»

Штучний інтелект та евристичний алгоритм А*
Підготувала
учениця 9-Б класу
ССЗШ № 37 м. Львова
Яричевська Я. І.
Керівник:
Галасюк А. В.

Штучний інтелект
Штучний інтелект – це наука, яка ставить своєю метою вивчення і моделювання атрибута людини, розділ комп'ютерної лінгвістики та інформатики, що займається формалізацією проблем та завдань, які нагадують завдання, виконувані людиною.
Будова нейронів людини.

Нейронні мережеві технології
ШНМ класифікують за:
1.t Типом вхідної інформації.
2.t Характером навчання.
3.t Характером налаштування
синапсів.
Штучні нейронні мережі (ШНМ) — математичні моделі, а також їхня програмна та апаратна реалізація, побудовані за принципом функціонування біологічних нейронних мереж — мереж нервових клітин живого організму. Системи, архітектура і принцип дії базується на аналогії з мозком живих істот. Ключовий елемент - штучний нейрон
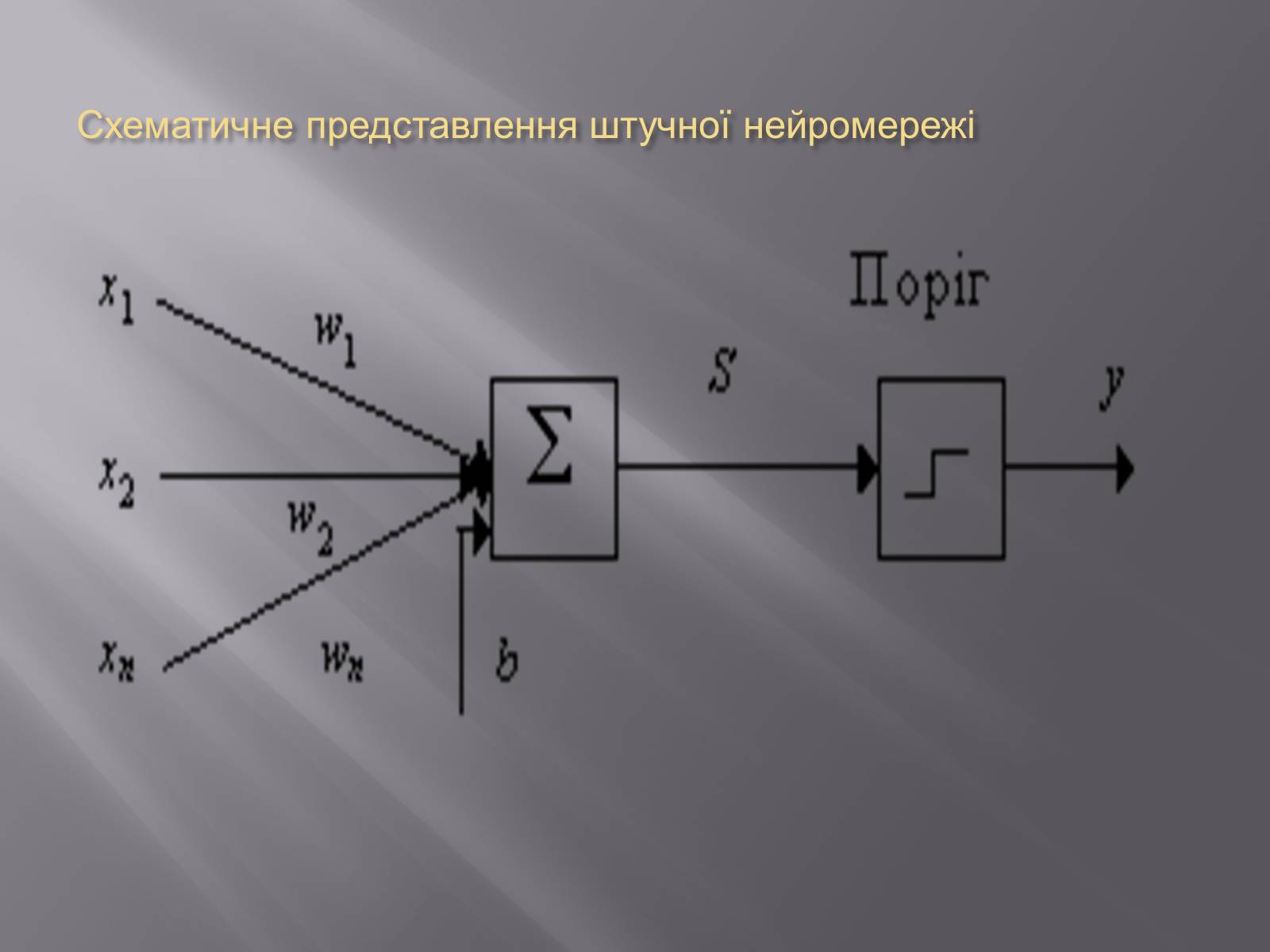
Схематичне представлення штучної нейромережі

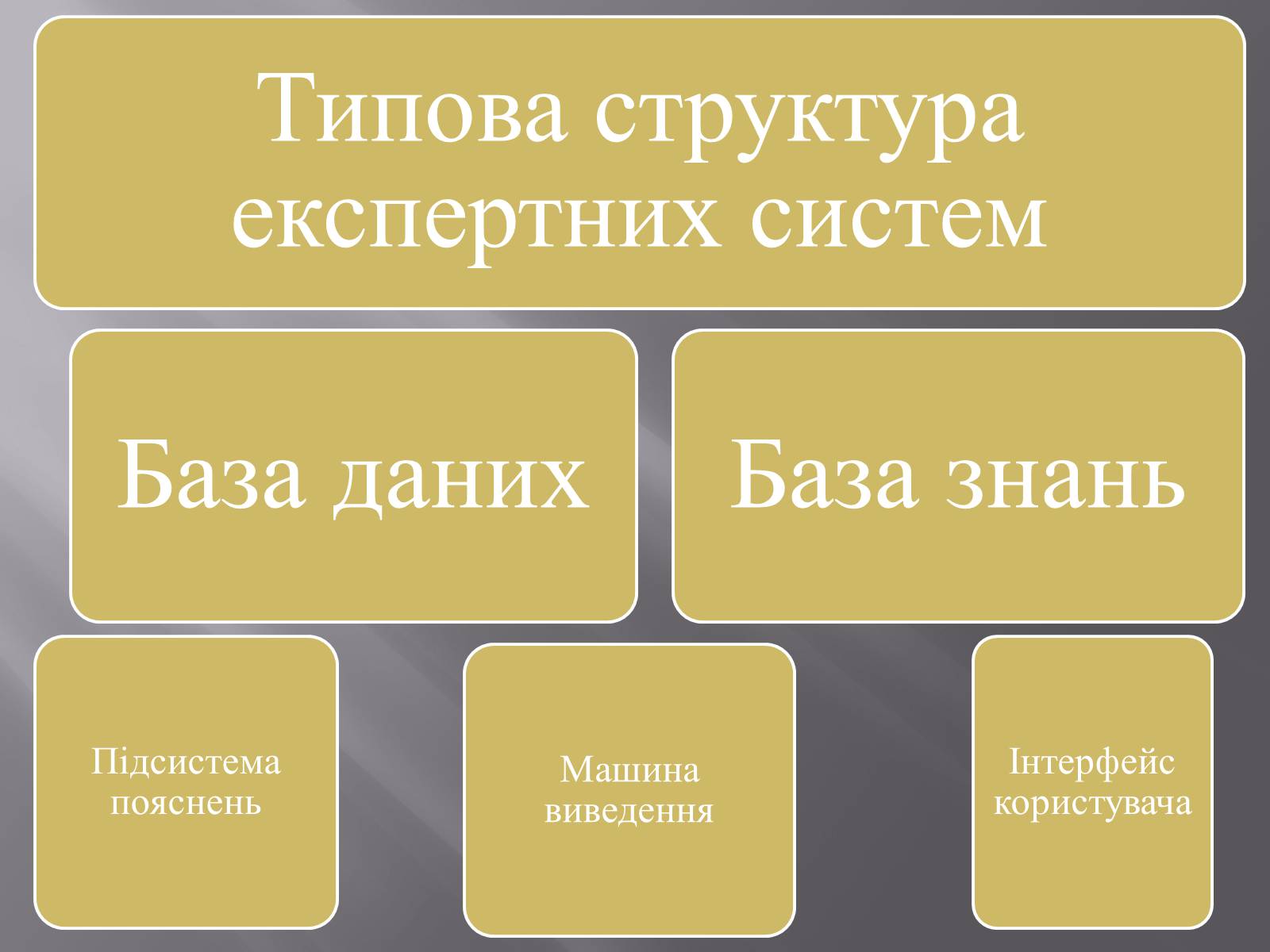
Інтелектуальні системи, засновані на знаннях
При опрацюванні на комп'ютері дані трансформуються і послідовно проходять такі етапи:
1.tДані, які існують як результат вимірів і спостережень.
2.tДані на матеріальних носіях інформації (таблицях, протоколах і т. д.)
3.tСтруктури даних у вигляді діаграм, графіків, функцій.
4.tДані, які містяться в комп'ютері і записані мовою опису даних.
5.tБази даних.

При опрацювання для комп'ютера знання трансформуються аналогічно до даних:
1.tЗнання, які існують в пам'яті людини як результат навчання, виховання, мислення.
2.tЗнання, поміщені на матеріальні носії (підручники, інструкції і т. д.)
3.tЗнання, описані мовами представлення знань.
4.tБази знань.
Етапи і технології розробки експертної системи
Експе́ртна систе́ма — це інтелектуальна комп'ютерна програма, що містить знання та аналітичні здібності одного або кількох експертів щодо деякої галузі застосування і здатна робити логічні висновки на основі цих знань, тим самим забезпечуючи вирішення специфічних завдань (консультування, навчання, діагностика, тестування, проектування тощо) без присутності експерта (спеціаліста в конкретній проблемній галузі).
Етапи і технології розробки експертної системи
Експе́ртна систе́ма — це інтелектуальна комп'ютерна програма, що містить знання та аналітичні здібності одного або кількох експертів щодо деякої галузі застосування і здатна робити логічні висновки на основі цих знань, тим самим забезпечуючи вирішення специфічних завдань (консультування, навчання, діагностика, тестування, проектування тощо) без присутності експерта (спеціаліста в конкретній проблемній галузі).
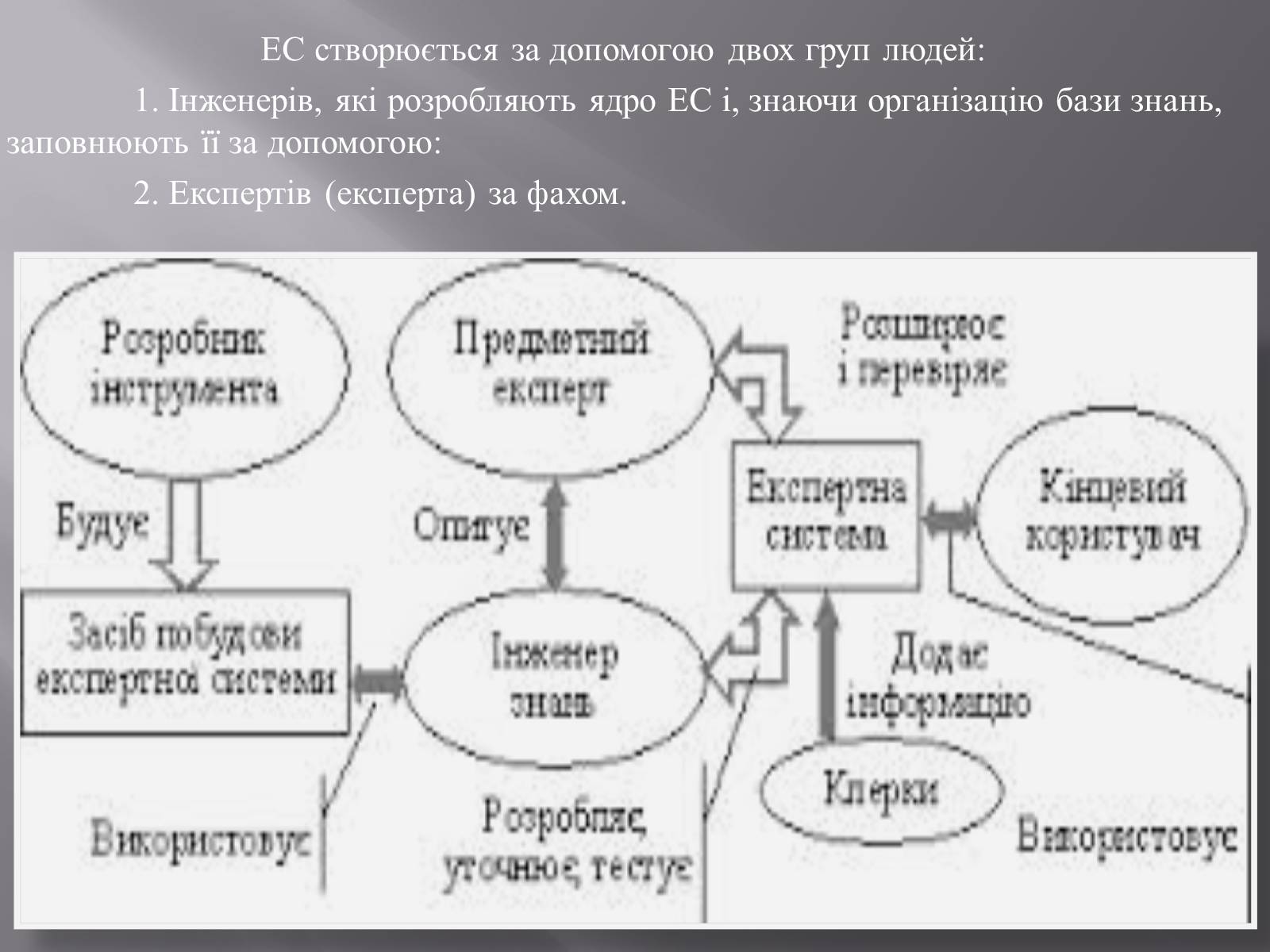
ЕС створюється за допомогою двох груп людей:
1. Інженерів, які розробляють ядро ЕС і, знаючи організацію бази знань, заповнюють її за допомогою:
2. Експертів (експерта) за фахом.

У процесі розробки експертні системи проходять певні стадії, урезультаті яких утворюються різні версії, які називаються прототипами:
•tДемонстраційний прототип
•tДослідницький прототип
•tДіючий прототип
•tПромислова експертна система
•tКомерційна експертна система
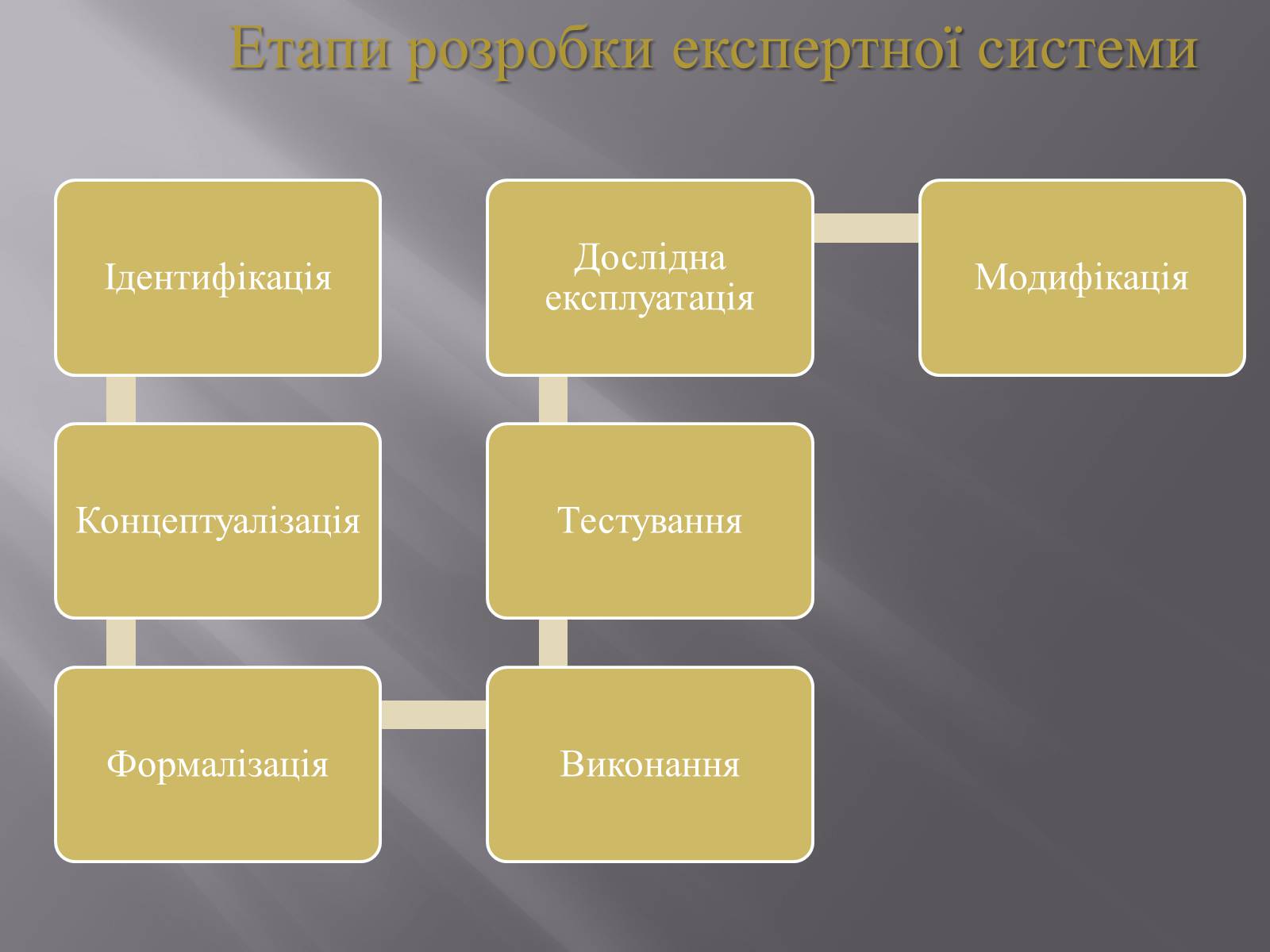
Етапи розробки експертної системи
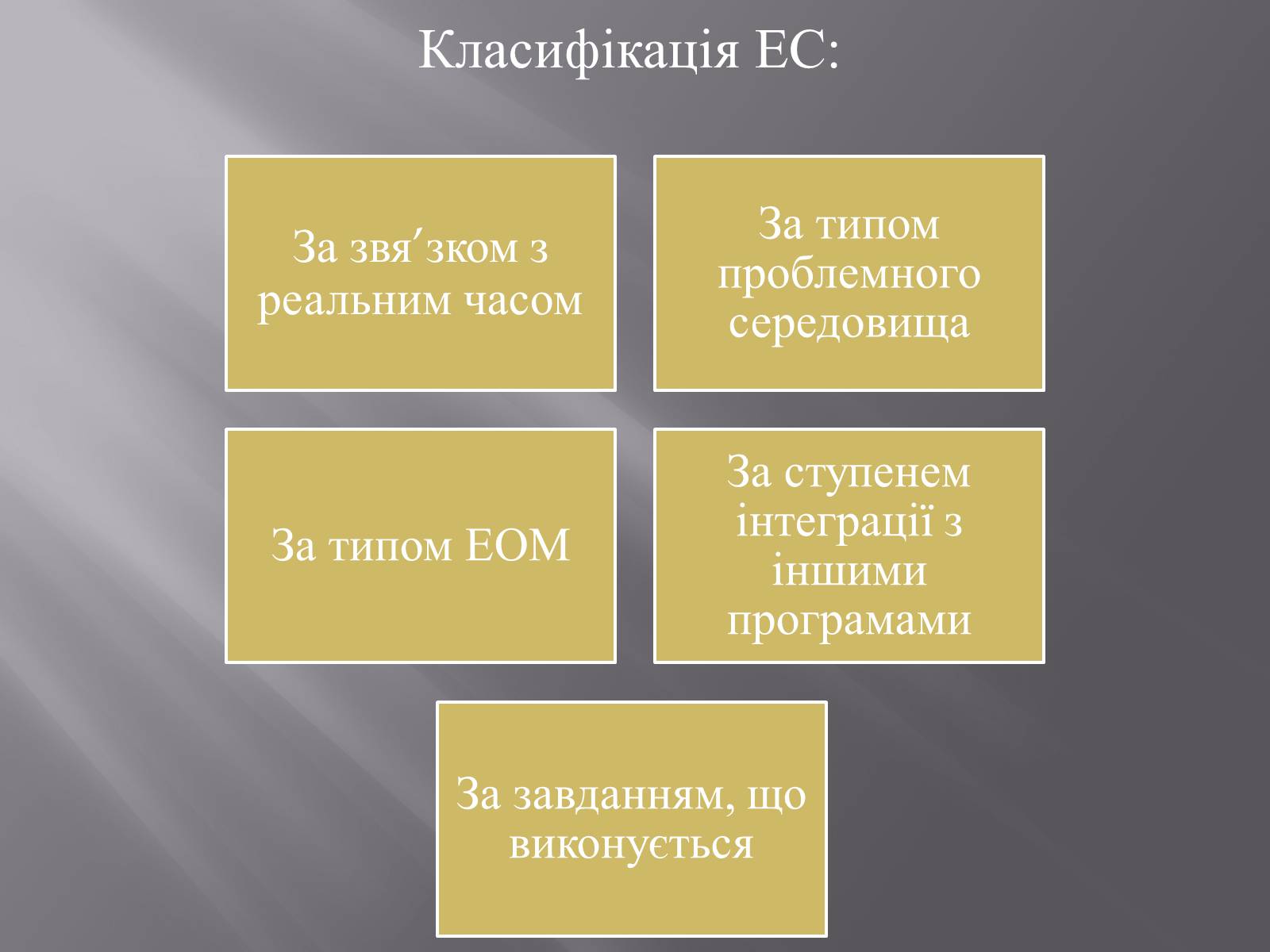
Класифікація ЕС:

Евристика. Евристичні моделі, методи та алгоритми
Евристика — наука, яка вивчає творчу діяльність, методи, які використовуються у відкритті нового і в навчанні. Евристичні методи (друга назва евристики) дозволяють пришвидшити процес розв'язання задачі. Метою евристики є побудова моделей процесу розв'язання якої-небудь нової задачі.

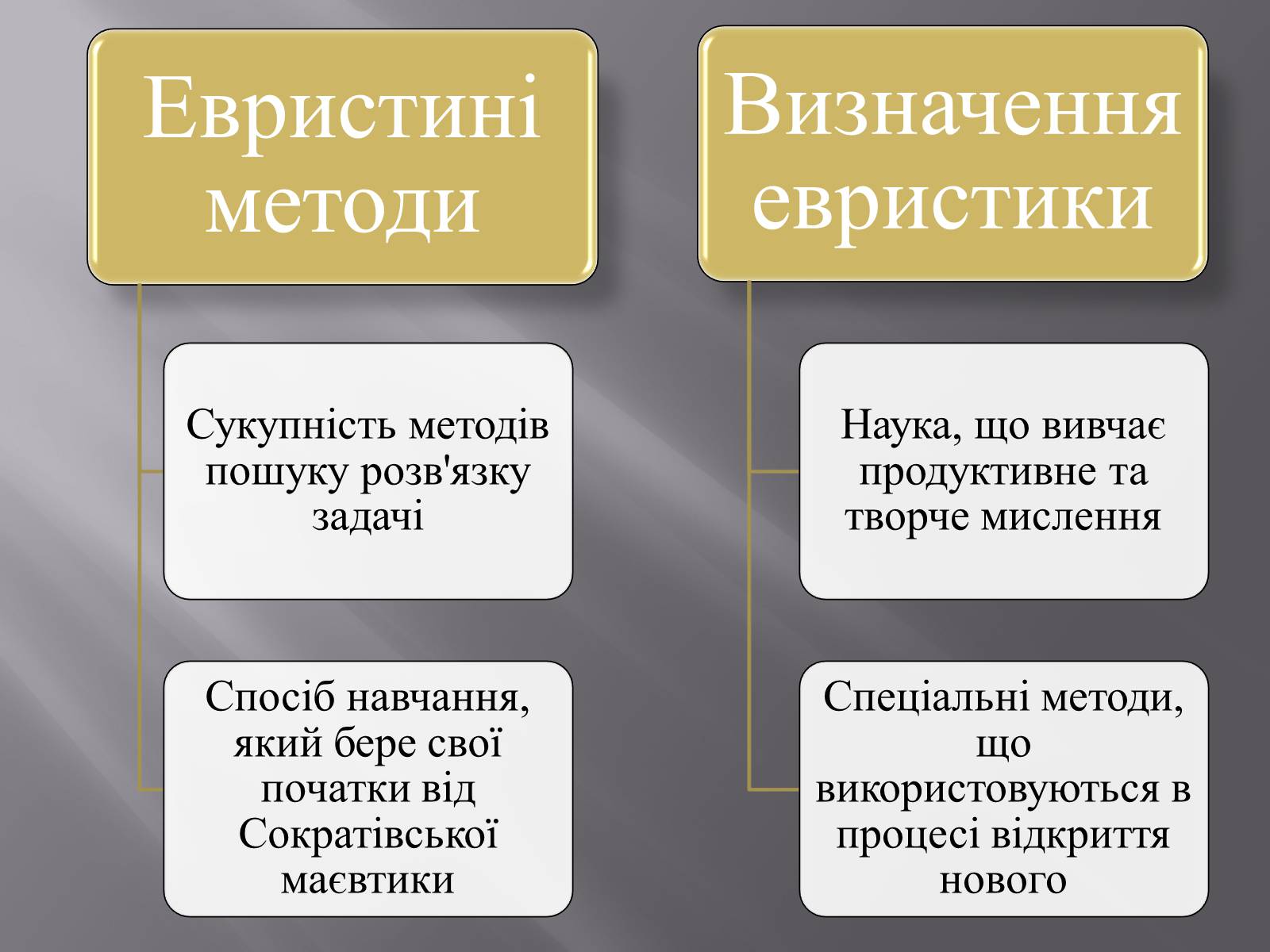
Також існують такі типи моделей:
•tМодель сліпого пошуку, яка спирається на так званий метод проб і помилок.
•tЛабіринтна модель, в якій задача розглядається як лабіринт, а процес пошуку розв'язку — як прохід лабіринтом.
•tСтруктурно-семантична модель, яка вважається в наш час найповнішою і яка відображає семантичні відношення між об'єктами, які складають область задачі.
Також існують такі типи моделей:
•tМодель сліпого пошуку, яка спирається на так званий метод проб і помилок.
•tЛабіринтна модель, в якій задача розглядається як лабіринт, а процес пошуку розв'язку — як прохід лабіринтом.
•tСтруктурно-семантична модель, яка вважається в наш час найповнішою і яка відображає семантичні відношення між об'єктами, які складають область задачі.
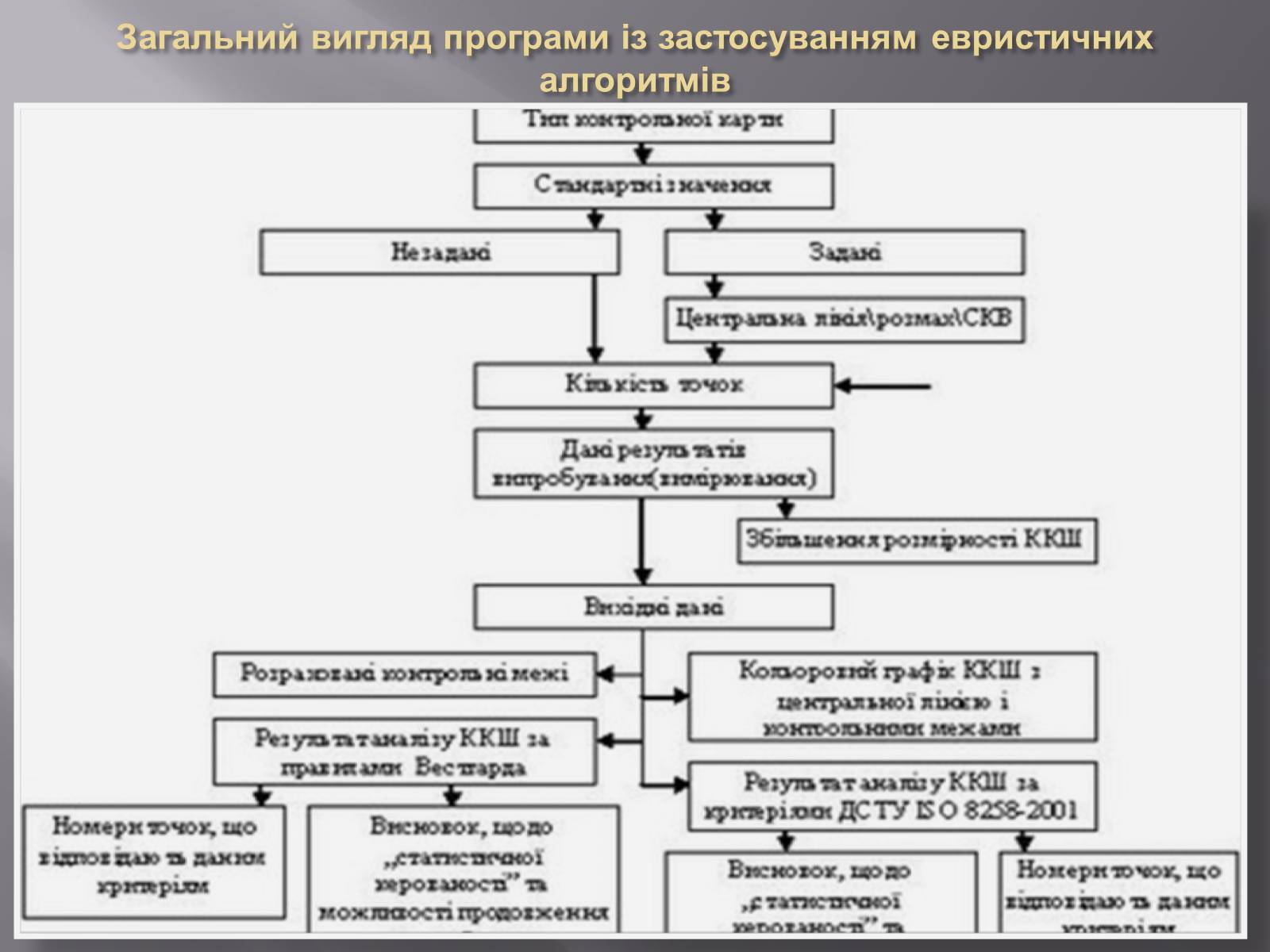
Загальний вигляд програми із застосуванням евристичних алгоритмів

Евристику використовують в багатьох сферах людського життя і, зокрема, в інформатиці. Чи, точніше, тут використовують евристичні алгоритми. В інформатиці — це алгоритми, спроможні видати прийнятне рішення проблеми серед багатьох рішень, але неспроможні гарантувати, що це рішення буде найкращим.
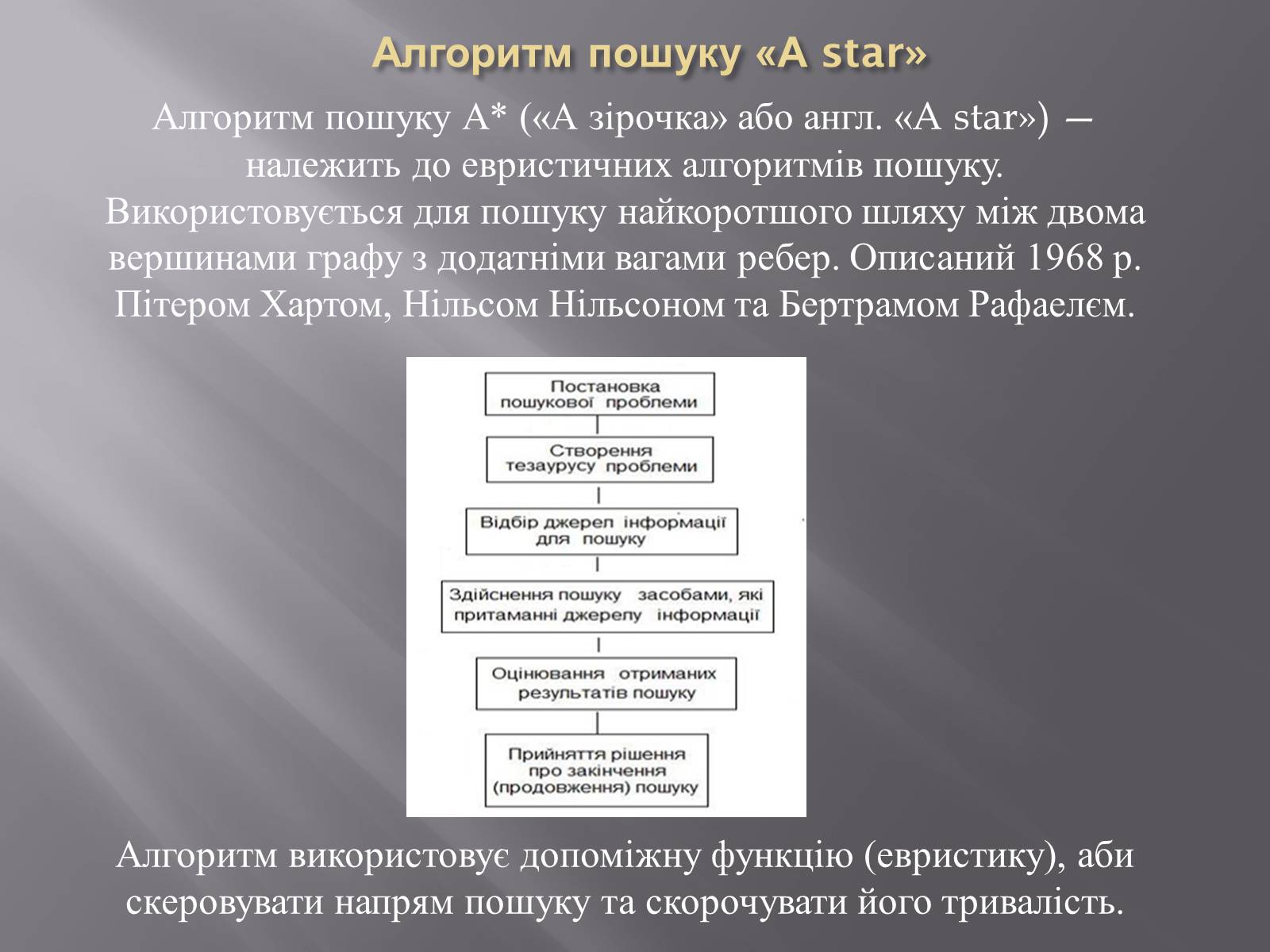
Алгоритм пошуку «А star»
Алгоритм пошуку А* («А зірочка» або англ. «A star») — належить до евристичних алгоритмів пошуку. Використовується для пошуку найкоротшого шляху між двома вершинами графу з додатніми вагами ребер. Описаний 1968 р. Пітером Хартом, Нільсом Нільсоном та Бертрамом Рафаелєм.
Алгоритм використовує допоміжну функцію (евристику), аби скеровувати напрям пошуку та скорочувати його тривалість.

Функція f(x) для вершини x визначається так:
f(x)=g(x)+h(x),
де g(x) функція, значення якої дорівнюють вартості шляху від початкової вершини до x,h(x) евристична функція, оцінює вартість шляху від вершини x до кінцевої.

Кожна відома або повністю досліджена вершина має вказівник на попередні вершини. Завдяки цьому вказівникові, можна пройти шляхом від цієї до початкової вершини. Коли вершину x буде повністю досліджено (або розкрито, релаксовано), суміжні з нею вершини додаються до списку відомих вершин, а сама вершина додається в список повністю досліджених. Вказівники на попередню вершину встановлюються на x. Алгоритм зупиняється коли кінцева вершина потрапляє до списку повністю досліджених вершин. Знайдений шлях відтворюється із допомогою вказівників на попередню вершину. Якщо список відомих вершин порожніє, то розв'язку задачі не існує і алгоритм припиняє пошук. Алгоритм пошуку А* знаходить оптимальний шлях між двома вершинами в графі. В залежності від функції вартості, яка задає кожному ребру його «вагу», оптимальність може означати найкоротший, найшвидший або навіть найпростіший шлях.
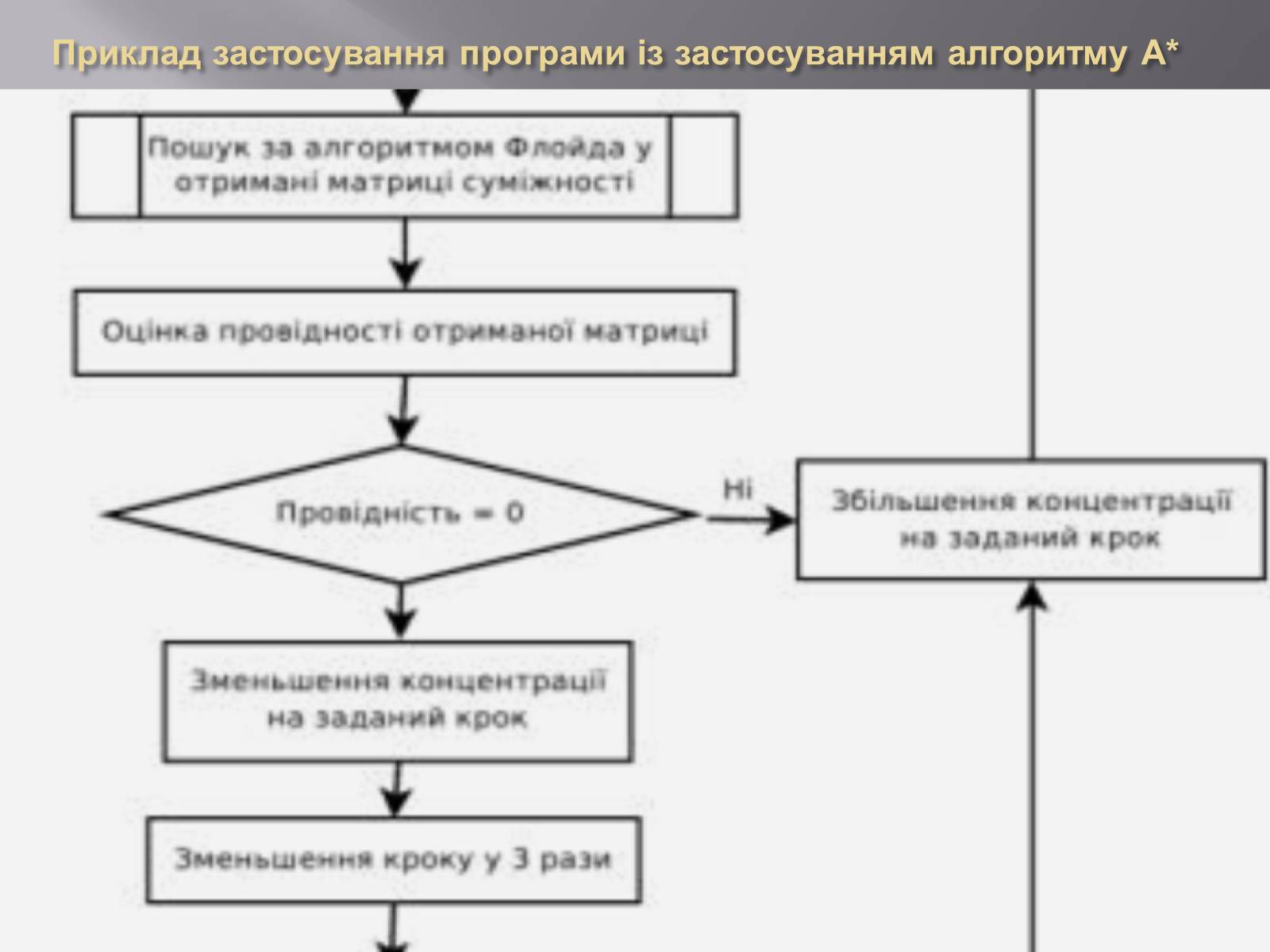
Приклад застосування програми із застосуванням алгоритму А*
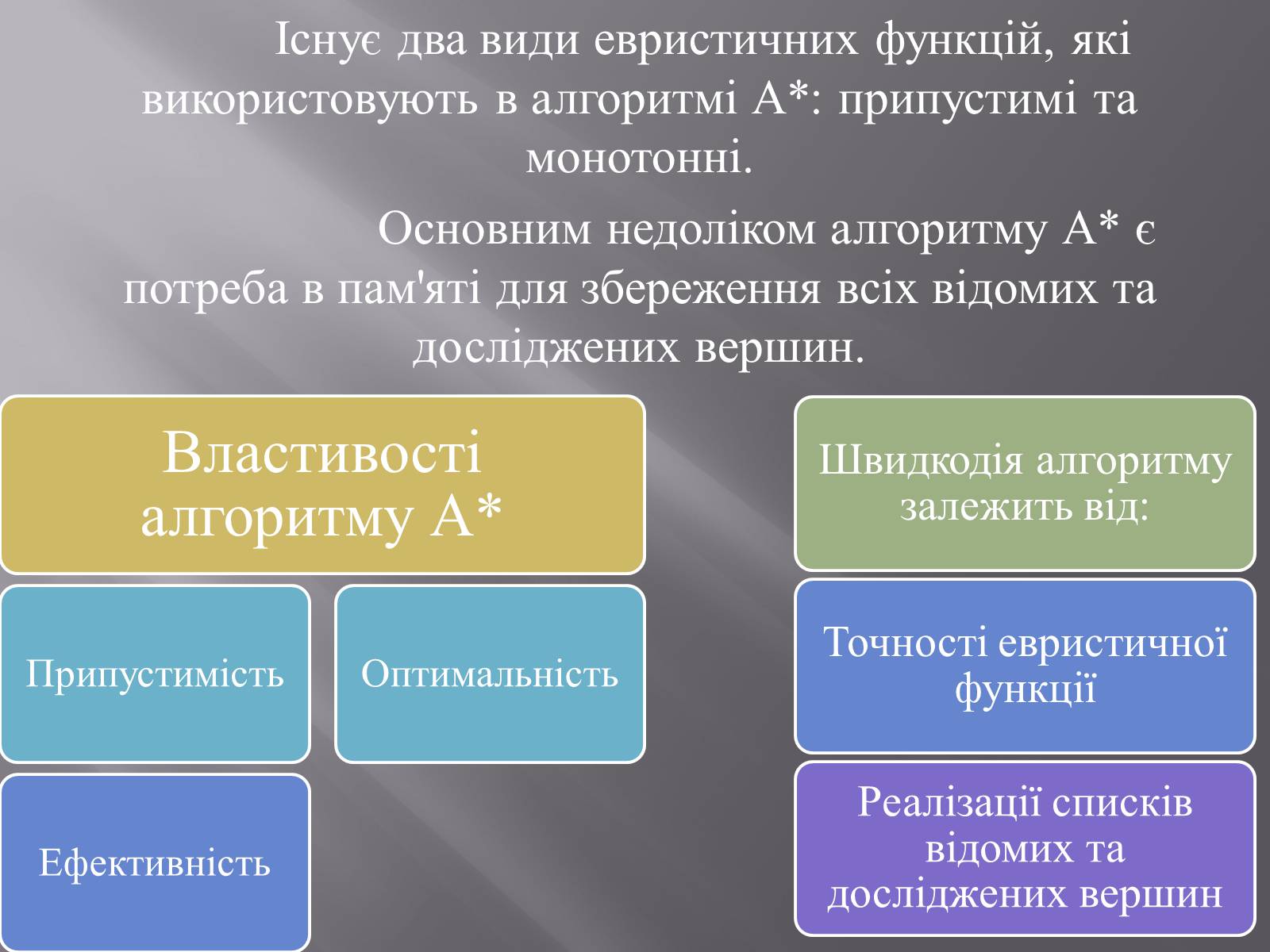
Існує два види евристичних функцій, які використовують в алгоритмі А*: припустимі та монотонні.
Основним недоліком алгоритму А* є потреба в пам'яті для збереження всіх відомих та досліджених вершин.

Принцип роботи алгоритму пошуку шляху А*
1. Поміщаємо в open-список стартовий вузол.
2. Основний цикл (доки open-список не пустий).
3. Беремо з open-списку верхній вузол.
4. Якщо цей вузол дорівнює кінцевому, то будуємо шлях і виходимо з основного циклу.
5. Обробляємо посилання вибраного вузла. Для кожного сусіда:
- перевіряємо його на проходимість, для конкретного юніта, якщо він непрохідний, то переходимо до наступного сусіда;
- обчислюємо оцінку шляху від початкового вузла через поточний до сусіда;
- шукаємо сусіда в open- і close-списках, якщо знайшли, то порівнюємо його оцінку шляху від стартового вузла з обчисленою, якщо його оцінка краща, то переходимо до наступного сусіда, у протилежному випадку видаляємо вузол із відповідного списку, перераховуємо оцінку шляху до кінцевого вузла і поміщаємо цього сусіда в open-список, у відповідне місце;
6. Поміщаємо поточний вузол у close-список.
7. Переходимо до пункту 3 (кінець основного циклу).

Способи оптимізації
1. Використання хеш-таблиць.
Найшвидшим пошуком володіють хеш-таблиці. Тому є доцільність застосувати їх до алгоритму А*. На жаль, стандартні списки (stl) неможливо використовувати з хеш-таблицею, тому необхідно написати свої. Основна ідея - зберігати в хеш-таблиці вказівник на ітератор списку.
2. SmartLOD.
Другий спосіб оптимізації – додаткові посилання або так званий "смартЛОД". Ідея в тому, щоб додати у вузол, окрім основних посилань, до безпосередніх сусідів додаткові. Якщо вузол знаходиться у деякій «вільній» зоні, у якій відсутні перешкоди, то з цього вузла можна зробити посилання до країв області. Розміри області можна варіювати в залежності від скласдності карти. Наприклад, для карт, що мають вигляд лабіринту, можна шукати області в радіусі від 8 до 4 клітинок. Ця оптимізація дала додатково до першої ще 10-15% приросту продуктивності.

Застосування алгоритму А*
Як приклад застосування алгоритму А* можна запропонувати популярну гру «П'ятнашки». Ціль гри — упорядкувати квадратики за цифрами, переміщаючи їх по коробці, бажано зробити якомога менше переміщень.
Увесь процес пошуку розв'язку в "П'ятнашках" можно представити як задачу пошуку на графі. Вершинами такого графа будуть позиції полів головоломки, отримані врезультаті переміщення квадратів. Пошук розв'язку можно звести до пошуку термінального стану ігрового поля. Нам уже відомо, що алгоритм A* передбачає наяність двох списків вершин графа: відкритого і закритого. У першому знаходяться вершини, які ще не перевірені алгоритмом, а в другому – ті, які вже зустрічалися в ході пошуку розв'язку.

На кожному новому кроці зі списку відкритих вершин обирається вершина з найменшою вагою. Вага f(x) кожної вершини обчислюється як сума відстаней від початкової до поточної вершини g(x) та евристичного припущення про відстань від поточної вершини до термінальної h(x). f(x) = g(x) + h(x), де x - поточна вершина (стан ігрового поля).
Для "П'ятнашок" можна зробити припущення, що для досягнення термінальної вершини необхідно виконати переміщень не менше, ніж кількість квадратиків, що знаходяться не на своїх місцях, а відстань від початкової до поточної вершини розраховувати як кількість здійснених перестановок.
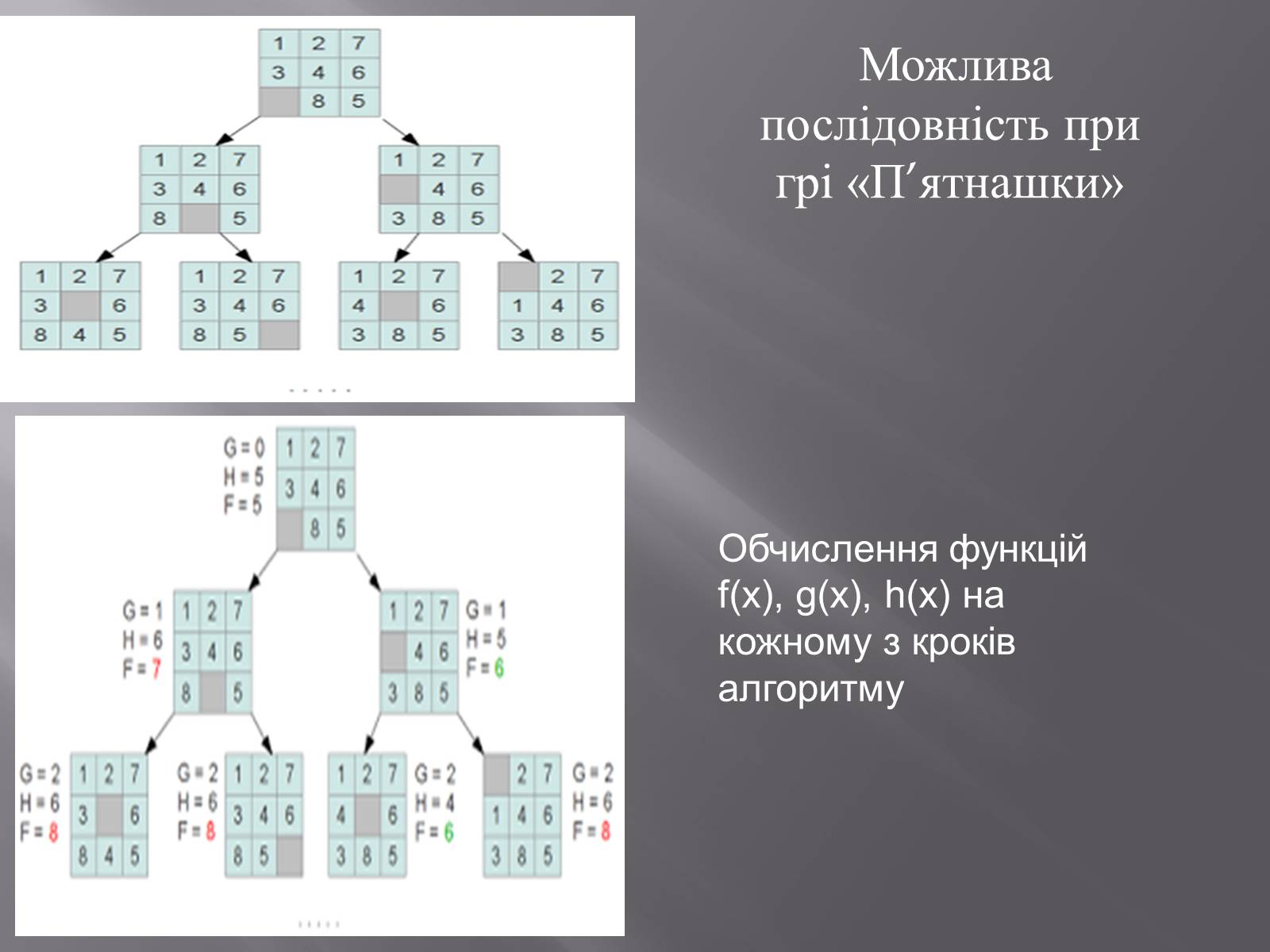
Обчислення функцій f(x), g(x), h(x) на кожному з кроків алгоритму
Можлива послідовність при грі «П'ятнашки»

Далі для вибраної вершини створюються дочірні вершини Кожна вершина має посилання на батьківську. Згодом виконується перебір дочірніх вершин. Кожна дочірня вершина перевіряється на предмет наявності у списку закритих. Якщо вершина не зустрічалася раніше, вона переміщається у список відкритих вершин. Для неї вираховують евристичну відстань до термінальної вершини і переобчислюють відстані від початкової вершини, адже є імовірність, що поточний шлях до цієї вершини виявиться коротшим, ніж знайдений раніше. Якщо шлях виявився коротшим, посилання на батьківську вершину змінюється. Послідовність дій повторюється, поки в списку відкритих вершин є хоча б одна вершина чи поки в ході виконання алгоритму не зустрінеться термінальна вершина.

Також вищезгадані задачі відрізняються правилами порождення дочірніх вершин, алгоритмом розрахунку відстані від початкової вершини і евристичною оцінкою відстані до термінальної вершини.
Алгоритм А* застосовується для розв'язання великого числа задач. Розглянемо загальну побудову алгоритму для кількох задач одночасно.
У першу чергу, задачі, що розв'язуються за допомогою алгоритму А*, відрізняються визначенням вершин графа (або станами). Уведемо абстрактний клас, інкапсулюючий загальну для будь-яких вершин, поведінку:

Даний розв'язок дещо не оптимальний. Інформація у списку закритих вершин надлишкова: нас ніколи не цікавлять деталі вершин із цього списку, а тільки факт приналежності деякої вершини до нього. Для цього достатньо зберігати не самі вершини, а значення їх хеш-функцій.
Що стосується реалізації безпосередньо «П'ятнашок», то, по-перше, саме ігрове поле зручно зображати одновимірним масивом - це дозволить уникнути зайвих вкладених циклів і в цілому спростить розв'язок. Алгоритм розкриття вершини (отримання її нащадків) у такому випадку виходить досить простим. Спочатку знаходиться індекс пустої клітинки, потім вираховується індекс квадратика, який буде переміщений на пусту клітинку. Її індекс вираховується як сума індекса пустої клітинки та індекса одного з її сусідів. Індекси сусідніх клітинок елементарні: для сусіда зліва це -1, для сусіда справа +1, для сусіда зверху -(розмір поля), для сусіда знизу +(розмір поля.
По-друге, для генерування початкового стану, перше, що зазвичай спадає на думку – це випадкове розташування клітинок на гральному полі. Але при такому підході є ризик згенерувати такий початковий стан, розв'язку для якого не існує взагалі чи пошук розв'язку затягнеться на досить довгий час. Можна піти іншим шляхом: виконувати N випадкових, коректованих перестановок квадратиків, починаючи з термінального стану.

Висновок
Повсякденна робота сучасного програміста рідко надає можливість розвитку творчого мислення. Найчастіше для вирішення задач достатньо застосувати уже відомий роз'язок: патерн чи бібліотеку. Знання загальноприйнятих підходів і практик, бібліотек і фреймворків, ось що сьогодні є ознакою кваліфікованого програміста. Між тим, краса і чарівність програмування для багатьох у повній мірі відкривається у вирішенні багатьох складних алгоритмічних задач, які так рідко зустрічаються в повсякденній практиці. Саме алгоритм А* допоміг мені вирішити декілька таких задач. А* належить до евристичних алгоритмів пошуку. Завдяки йому я краще зрозуміла штучний інтелект та сферу його застосування в цілому, гру «П'ятнашки» і показав мені наскільки цікавими є евристика, штучні нейронні мережі та штучний інтелект і, я гадаю, допоміг мені вибрати майбутню професію.