Презентація на тему «Прості механізми» (варіант 1)
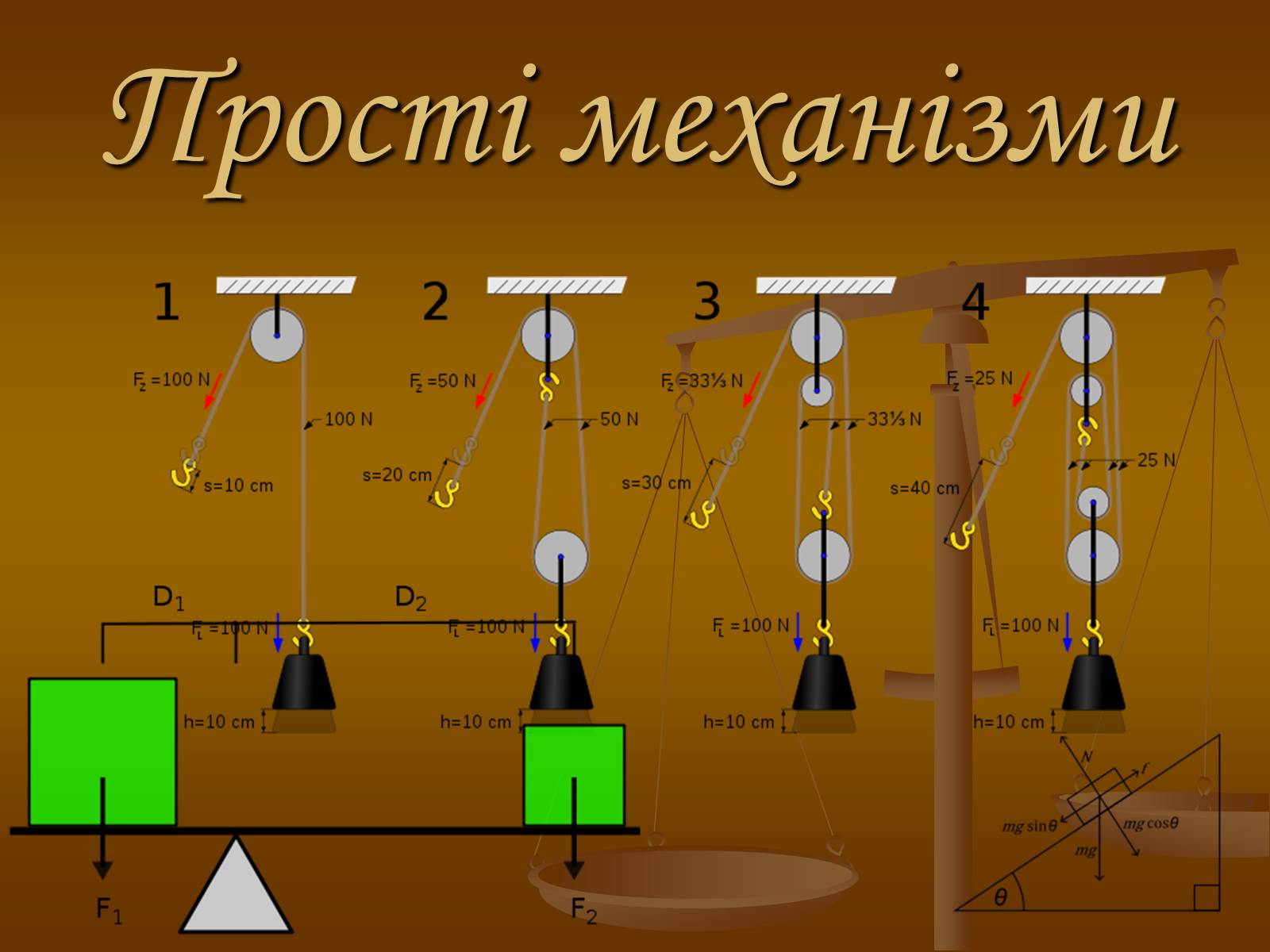
Прості механізми

Важіль
Простий механізм, тверде тіло, що може обертатися навколо певної точки, яка називається точкою опори. Застосовується для підйому вантажів.
Віддаль від точки опори до точки, в якій прикладена сила, називається плечем важеля. Зазвичай у важеля два різних плеча: до одного плеча прикладається зусилля, на інше діє вага вантажа.

Принцип дії
Принцип дії важеля оснований на основних законах статики. Статична рівновага досягається тоді, коли алгебраїчна сума добутків сили на плече дорівнює нулю.
де Fi — прикладена сила, Di — відповідне плече. Сили потрібно брати зі знаком плюс, якщо вони намагаються повернути важіль в один бік (наприклад, за годинниковою стрілкою), і зі знаком мінус, якщо вони намагаються повернути його в протилежний бік.

Типи важелів
1. У важелі першого типу точки прикладення сил лежать з різних боків від точки опори. Одна з сил намагається повернути важель за годинниковою стрілкою, інша — проти годинникової стрілки. Для того, щоб отримати виграш у силі, потрібно, щоб плече, до якого прикладена сила, було довшим за плече навантаження.

2. У важелі другого типу обидві точки прикладення сил лежать по один бік від точки опори і тягар має менше плече. Щоб підняти тягар, необхідно направити силу вгору. Приклади таких важелів — тачка, лом.
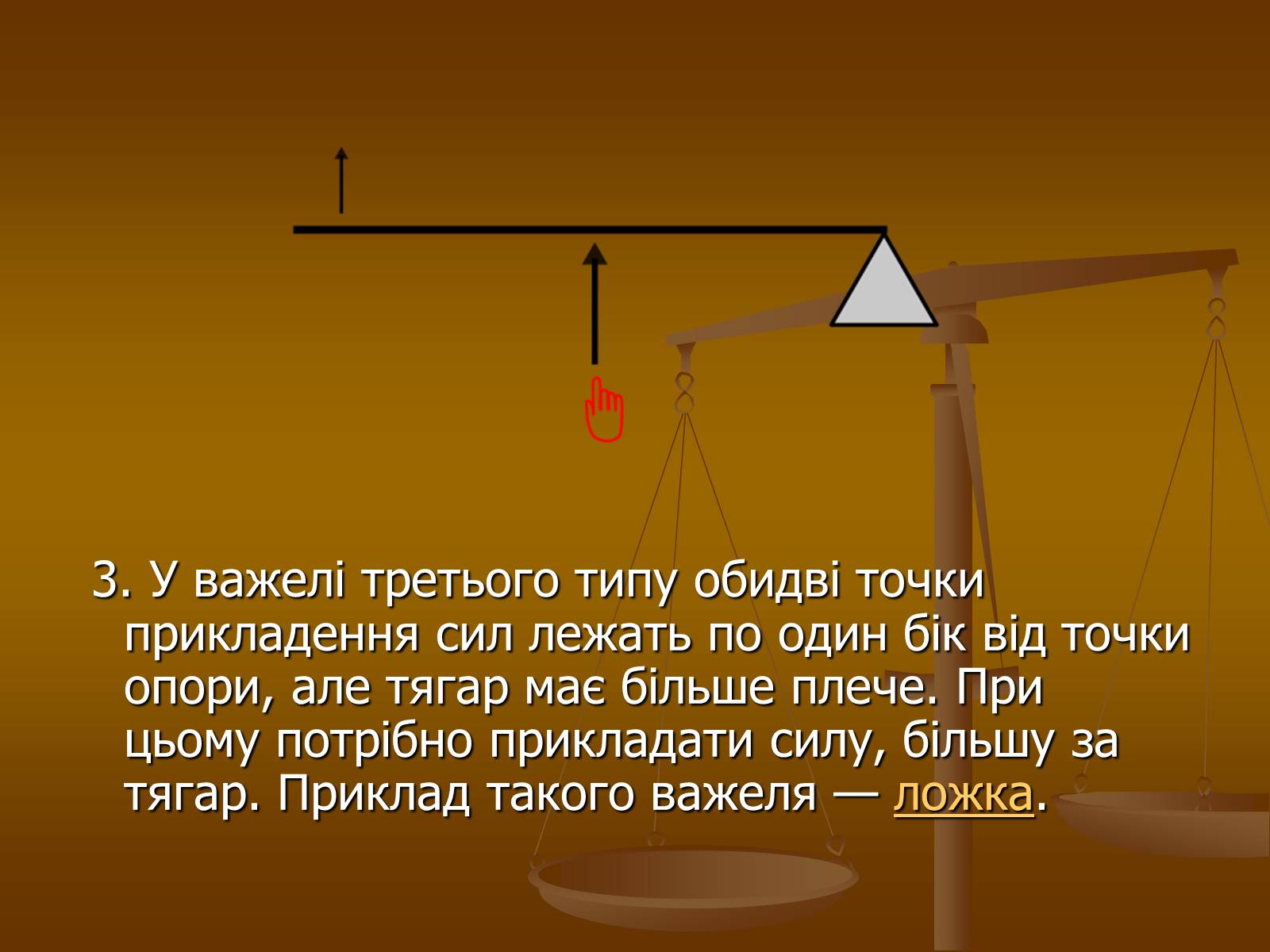
3. У важелі третього типу обидві точки прикладення сил лежать по один бік від точки опори, але тягар має більше плече. При цьому потрібно прикладати силу, більшу за тягар. Приклад такого важеля — ложка.

Виграш у швидкості
В метальних знаряддях,
наприклад, катапультах використовується виграш у
швидкості. Оскільки кут повороту обох пліч важеля
однаковий, то віддаль, яку проходить за певний час
довший кінець більша, ніж віддаль, яку проходить
коротший кінець. Математично це твердження можна
виразити формулою
Таким чином, приладаючи силу до коротшого кінця й
змушуючи його рухатися, можна водночас досягти
дуже високої швидкості довшого кінця, що потрібно для
метання снарядів.

Історія
Важіль використовувався людством з
древніх часів, а от повністю зрозумів і
зумів сформулювати принцип дії цього
простого механізму Архімед. Йому
належить крилатий вираз "Дайте меті
точку опори, і я переверну Землю" .

Блок
Блок - простий механічний пристрій, що дозволяє регулювати силу, вісь
якого закріплена при підйомі вантажів, не піднімається і не опускається.
Являє собою колесо з жолобом по колу, що обертається навколо своєї
осі. Жолоб призначений для каната, ланцюга, ременя і т. п. Вісь блоку
міститься в обіймах, прикріплених на балці або стіні, такий блок
називається нерухомим, коли ж до цих обойма прикріплюється вантаж, і
блок разом з ними може рухатися, то такий блок називається рухомим.

Нерухомий блок
Нерухомий блок вживається для підйому невеликих вантажів або для зміни напрямку сили.
Умова рівноваги блоку:
, де
F - додаваєме зовнішнє зусилля, m - маса вантажу, g - прискорення сили тяжіння, f - коефіцієнт опору в блоці (для ланцюгів приблизно 1.05, а для мотузок - 1.1). При відсутності тертя для підйому потрібна сила, рівна вазі вантажу.

Рухомий блок
Рухомий блок має вільну вісь і призначений для зміни величини прикладених зусиль. Якщо кінці мотузки, охоплюючий блок, складають з горизонтом рівні між собою кути, то діюча на вантаж сила належить до його вагою, як радіус блоку до хорди дуги, обхопленной канатом; звідси, якщо мотузки паралельні (тобто коли дуга, охоплює мотузкою, дорівнює напівокружності), то для підйому вантажу сили буде потрібно вдвічі менше, ніж вагу вантажу, тобто:
При цьому вантаж пройде відстань, удвічі менше пройденого точкою прикладання сили F, відповідно, виграш у силі рухомого блоку дорівнює 2.

Похила площина
Похи́ла площина́ — один із простих механізмів, призначений для зменшення сили, за допомогою якої можна підняти вантаж на висоту.

Сили, які діють на тіло
Баланс сил, що діють на тіло на похилій
площині зображено на рисунку праворуч.
Силу тяжіння, направлена вертикально
вниз, можна розкласти на дві складові:
складову паралельну похилій площині, й
складову, перперндикулярну похилій
площині. Складова сили, яка перпендикулярна
до похилої площини, урівноважується силою
реакції N, а та складова, що тягне тіло вниз
дорівнює , де m —
маса тіла, а g — прискорення вільного падіння.
Оскільки sinθ < 1, то для того, що урівноважити
цю силу, потрібно прикласти силу меншу за вагу
тіла в умовах, коли воно лежить на
горизонтальній опорі (mg). Чим менший кут θ —
тим меншу потрібно прикладати силу, і тим
більший шлях повинно пройти тіло.

При русі тіла вгору, навіть у випадку, коли цей рух
рівномірний, руху перешкоджає також сила тертя , яку
можна оцінити за формулою
В цьому випадку для рівномірного руху тіла вгору
необхідно прикласти силу
Ця сила все ж менша за mg.
Щодо роботи, яку необхідно виконати для підйому тіла,
то похила площина не дає жодного виграшу. Навпаки,
частина затрачених зусиль йде на подолання сили
тертя.

Рівновага тіла на похилій площині
Якщо до тіла не прикладати жодної зовнішньоїсили, то воно може
залишатися на похилій площині в стані спокою, або скотитися вниз.
Оскільки потенційний чи дійсний рух тіла втакому випадку спрямований
вниз, то сила тертя діє проти паралельної до площини складової
сили тяжіння. Умовою рівноваги стає вираз
або, спрощуючи
Якщо коефіцієнт тертя менший за тангенс кута θ, то тіло зісковзуватиме
вниз. Якщо більший, то тіло залишатиметься на похилій площині. Ця
умова не залежить від маси тіла.
Якщо коефіцієнт тертя менший за тангенс кута θ, то тіло зісковзуватиме
вниз. Якщо більший, то тіло залишатиметься на похилій площині. Ця умова
не залежить від маси тіла.

Похилу площину можна
використати для
Дослідження
рівноприскореного руху.
Рівнодійна сил, які діють
на тіло на похилій
площині, направлена
паралельно площині і
дорівнює, якщо знехтувати силами
тертя,
Тіло, що скочується з похилої
площини матиме прискорення
.
При малих кутах при
основі похилої площини,
це прискорення можна
зробити малим, що
дозволяє спостерігати, як тіло
набирає швидкість, тобто які
відрізки воно проходить за рівні
проміжки часу. Такі
дослідження провів Галілео
Галілей, визначивши, що
прискорення тіла не залежить
від його маси.
Прискорення тіла, що скочується похилою площиною

Похила площина в природі й техніці
Похилі площини часто
зустрічаються в повсякденному
житті. Наприклад, для пійому
вантажів
використовуються пандуси. Завдяки
нахилу пандуса сила, необхідна для
збільшення висоти менша, хоча шлях,
який потрібно подолати, збільшується.
Менш очевидно те, що на принципі
похилої площини ґрунтується дія інших
простих механізмів: клину і гвинта. У
випадку клину використовується
похила площина з дуже гострим кутом.
У випадку гвинта різь теж є
викривленою похилою площиною.
Київський фунікулер у 1910 р.