Презентація на тему «Правильні многогранники» (варіант 5)

Правильні многогранники
Корєшкова А. В.
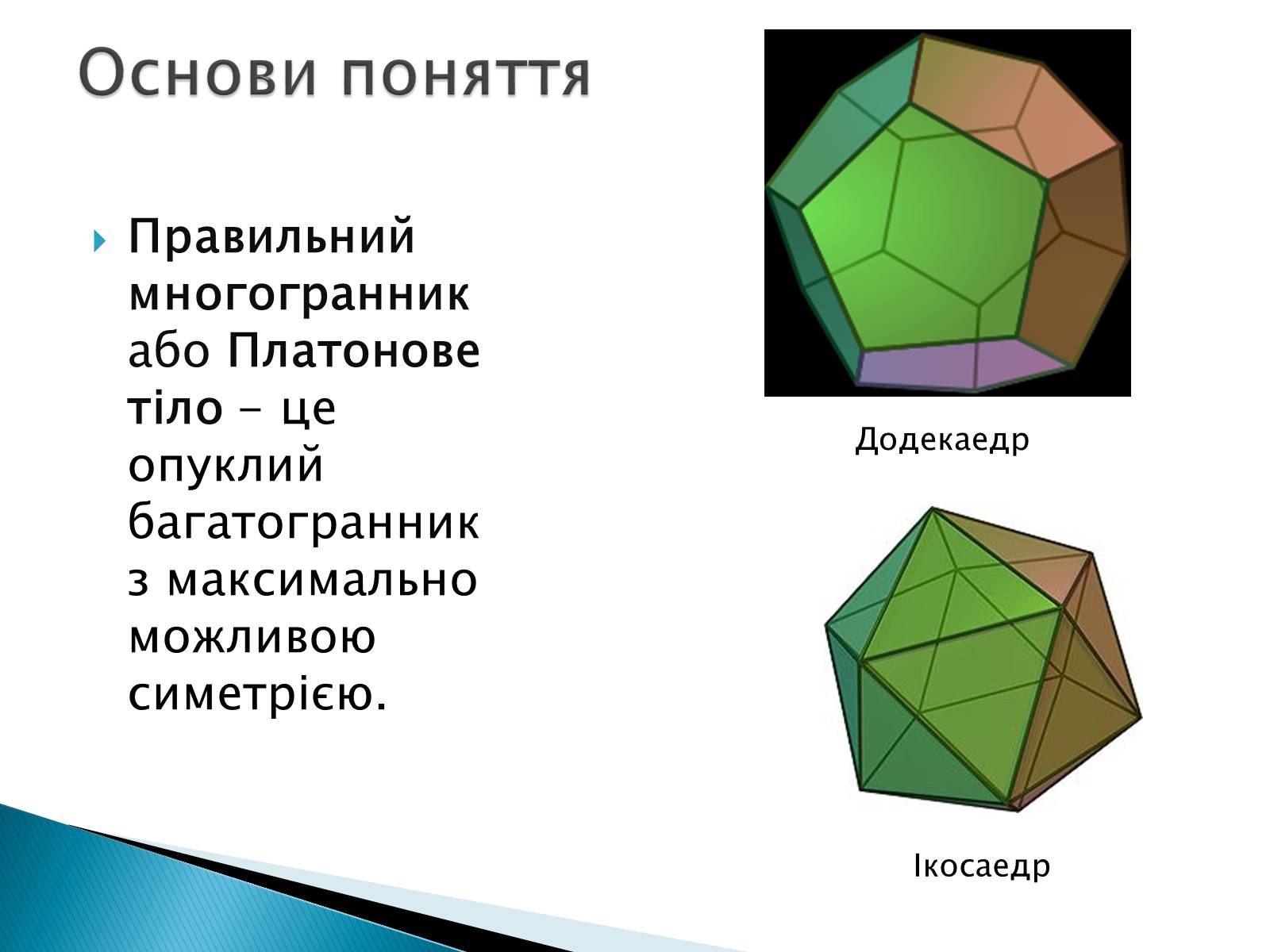
Правильний многогранник або Платонове тіло - це опуклий багатогранник з максимально можливою симетрією.
Основи поняття
Додекаедр
Ікосаедр

Багатогранник називається правильним, якщо:
він опуклий;
всі його грані є рівними правильними багатокутниками;
в кожній його вершині сходиться однакове число граней;
всі його двогранні кути рівні.
Основні ознаки
Розгортка ікосаедра
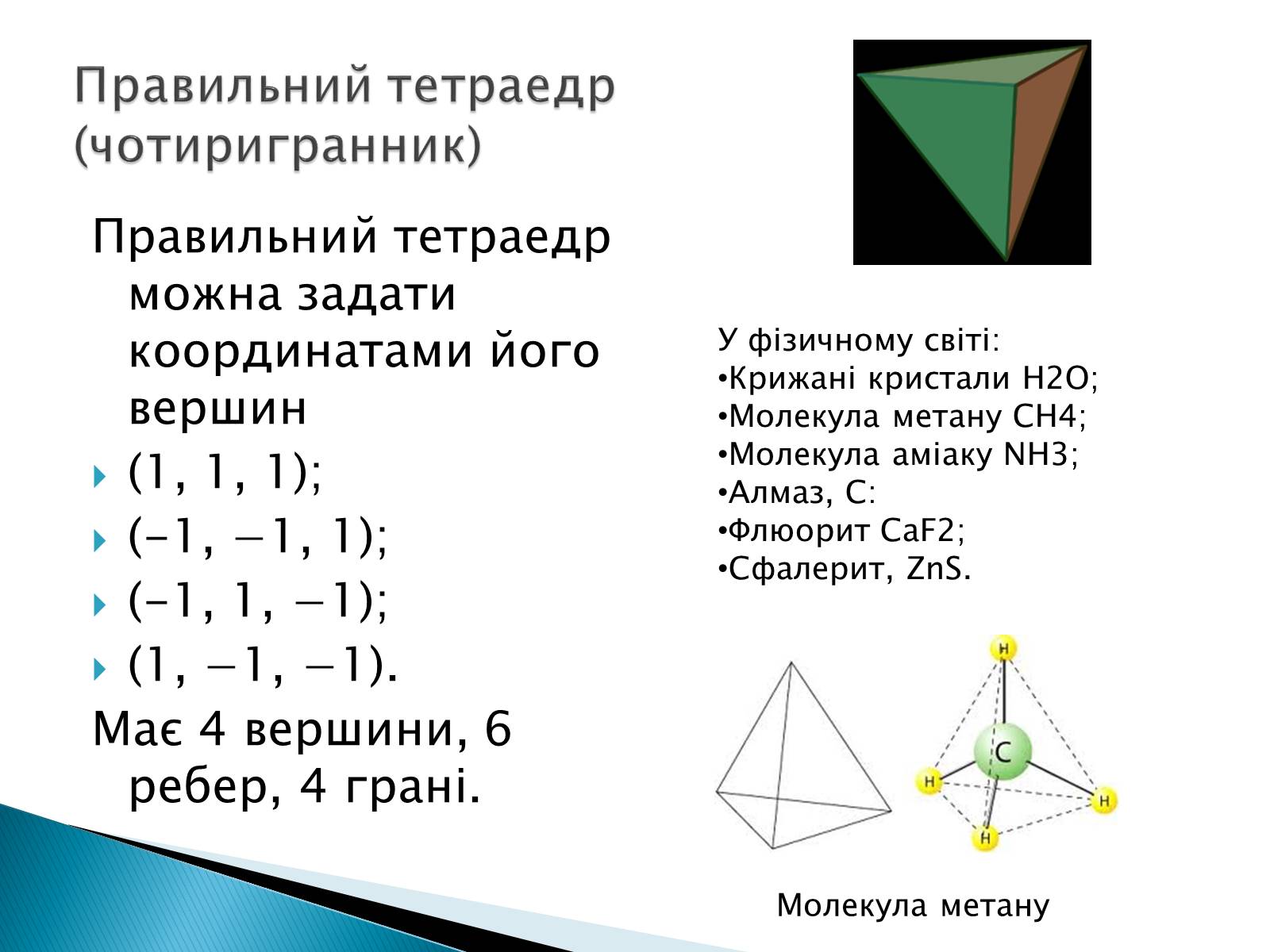
Правильний тетраедр можна задати координатами його вершин
(1, 1, 1);
(-1, −1, 1);
(-1, 1, −1);
(1, −1, −1).
Має 4 вершини, 6 ребер, 4 грані.
Правильний тетраедр (чотиригранник)
У фізичному світі:
Крижані кристали H2O;
Молекула метану CH4;
Молекула аміаку NH3;
Алмаз, C:
Флюорит CaF2;
Сфалерит, ZnS.
Молекула метану

Куб або гексаедр — правильний багатогранник, кожна грань якого є квадратом. Має 8 кутів, 12 ребер, 6 граней.
Куб
Властивості куба:
В куб можна вписати тетраедр двома способами, притому чотири вершини тетраедра будуть суміщено з чотирма вершинамі куба. Всі шість ребер тетраедра лежатимуть на всіх шести гранях куба і дорівнюватимуть діагоналі грані-квадрата.
Чотири перетини куба є правильними шестикутниками — ці перетини проходять через центр куба перпендикулярно чотирьом його діагоналям.

Октаедр має 8 граней (трикутних), 12 ребер, 6 вершин (у кожній вершині сходяться 4 ребра).
Октаедр
У формі октаедра кристалізуються мідь, срібло, алмаз, магнетит, флюорит тощо.

Додекаедр (від грец. dodeka — дванадцять і грец. hedra — грань) — правильний багатогранник, об'ємна геометрична фігура, складена з дванадцяти правильних п'ятикутників. Кожна вершина додекаедра є вершиною трьох правильних п'ятикутників. Таким чином, додекаедр має 12 граней (п'ятикутних), 30 ребер і 20 вершин (у кожній сходяться 3 ребра). Сума плоских кутів при кожній з 20 вершин рівна 324°.
Додекаедр
Кристал піриту
Додекаедр
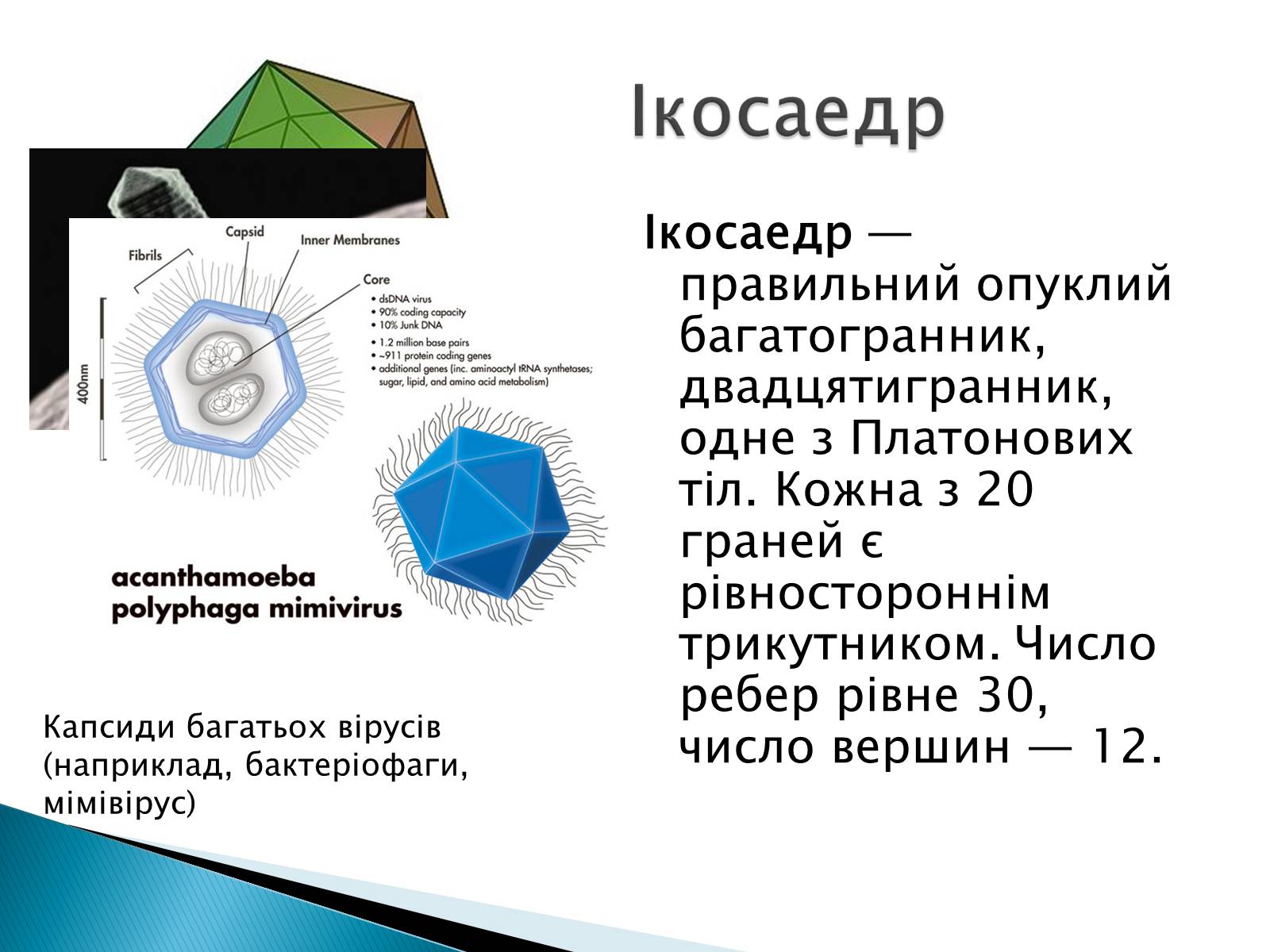
Ікосаедр — правильний опуклий багатогранник, двадцятигранник, одне з Платонових тіл. Кожна з 20 граней є рівностороннім трикутником. Число ребер рівне 30, число вершин — 12.
Ікосаедр
Капсиди багатьох вірусів (наприклад, бактеріофаги, мімівірус)

Правильні багатогранники названі по імені Платона, який в творі «Тімей» (нібито IV століття до н. е.) давав їм містичний смисл, але вони були відомі і до Платона;
Кеплер намагався побудувати модель Сонячної системи вписуючи і описуючи правильні багатогранники в сфери. Це вдалося йому не повністю, але послужило поштовхом до розробки Законів Кеплера.
Історія
Платон
Йоганн Кеплер

http://www.georgehart.com/virtual-polyhedra/vp.html
http://www.korthalsaltes.com/
http://www.mathconsult.ch/showroom/unipoly/
http://mathworld.wolfram.com/Octahedron.html
http://www.flickr.com/photos/pascalin/sets/72157594234292561/
Джерела