Презентація на тему «Призма» (варіант 2)
Призма
Пошукова робота
Виконав учень 11-го класу –
Петрунецький В.Д.
Парище - 2014
Призма
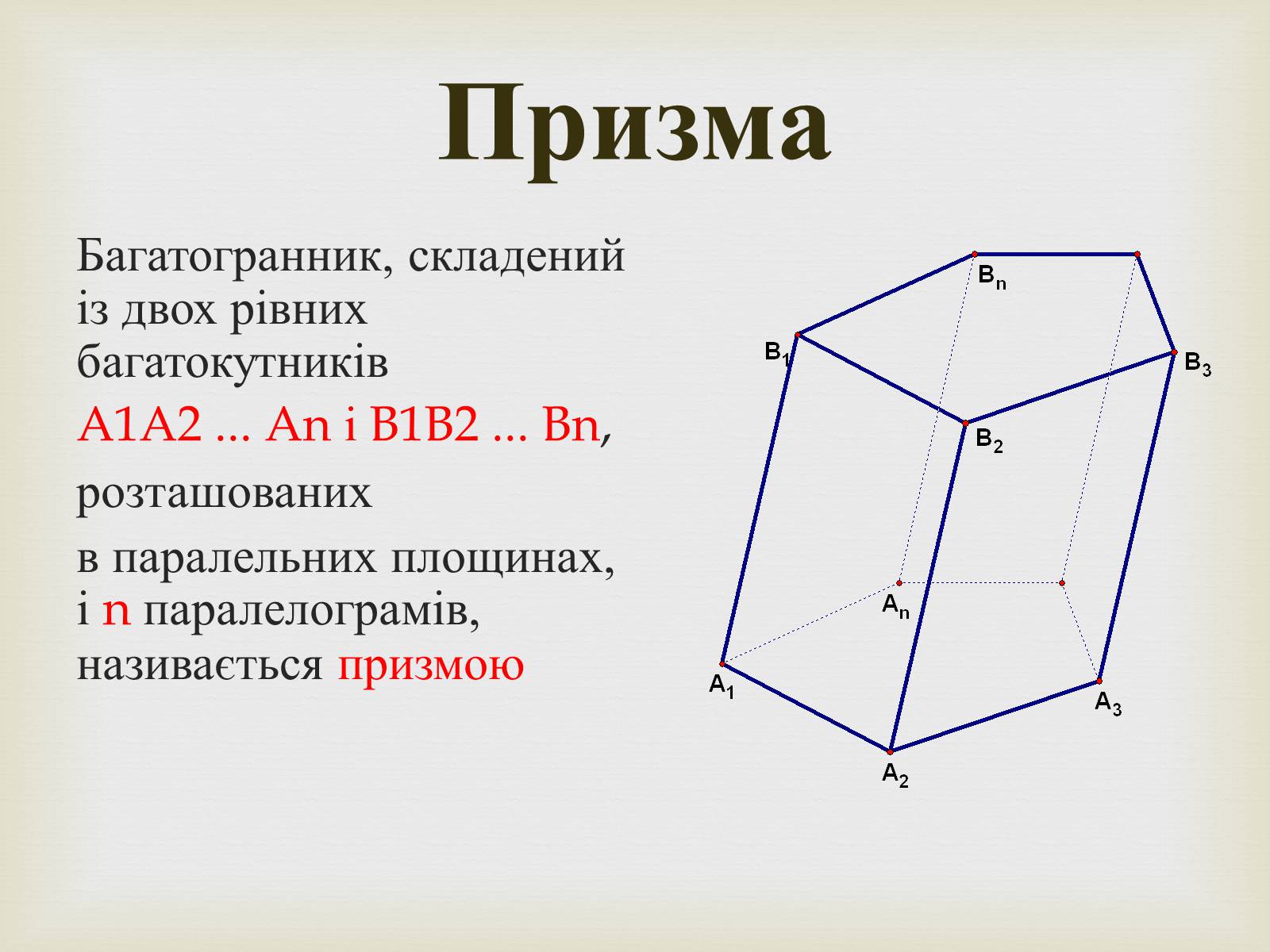
Багатогранник, складений із двох рівних багатокутників
A1A2 ... An і B1B2 ... Bn,
розташованих
в паралельних площинах, і n паралелограмів, називається призмою
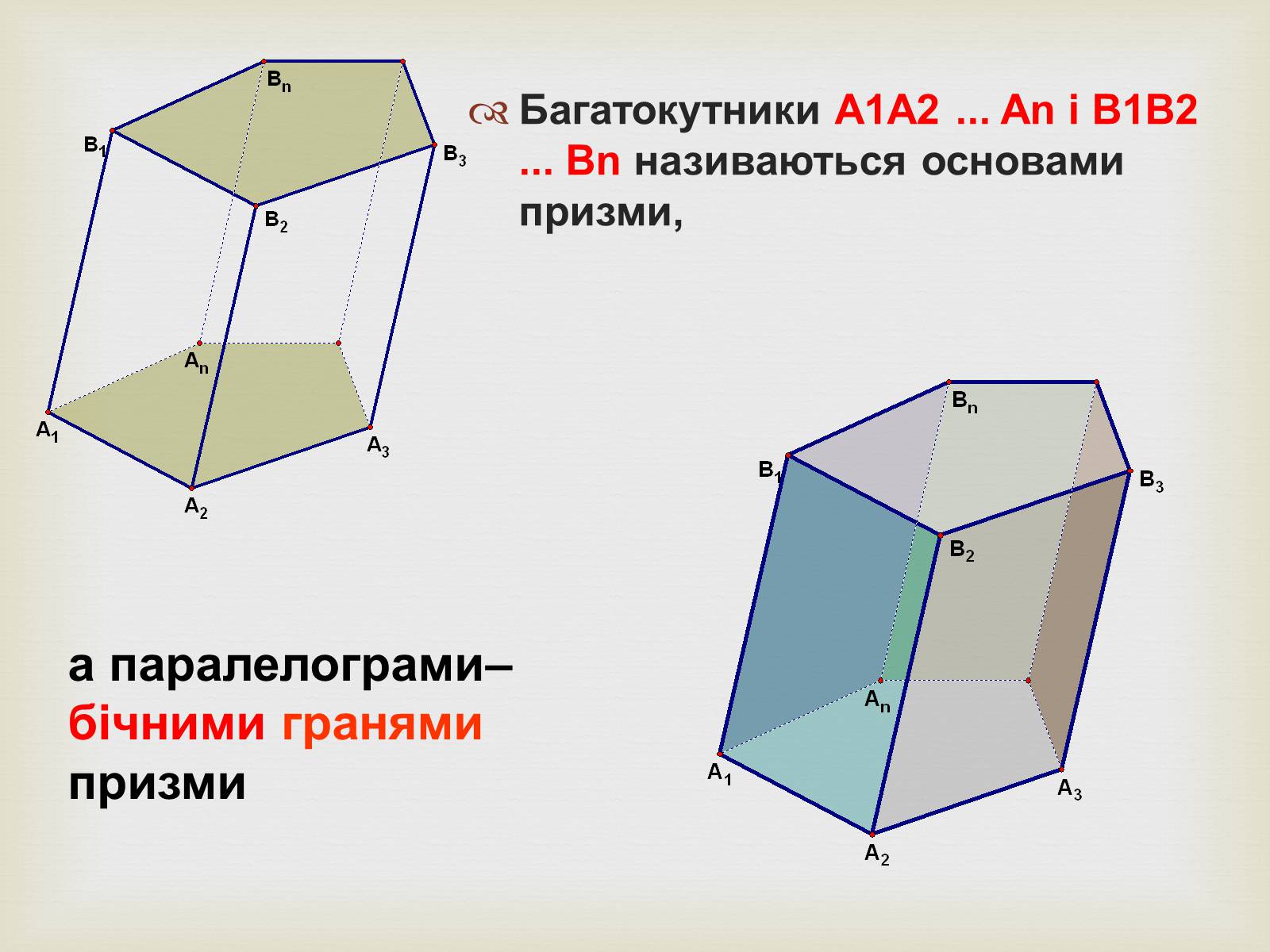
Багатокутники A1A2 ... An і B1B2 ... Bn називаються основами призми,
а паралелограми– бічними гранями призми
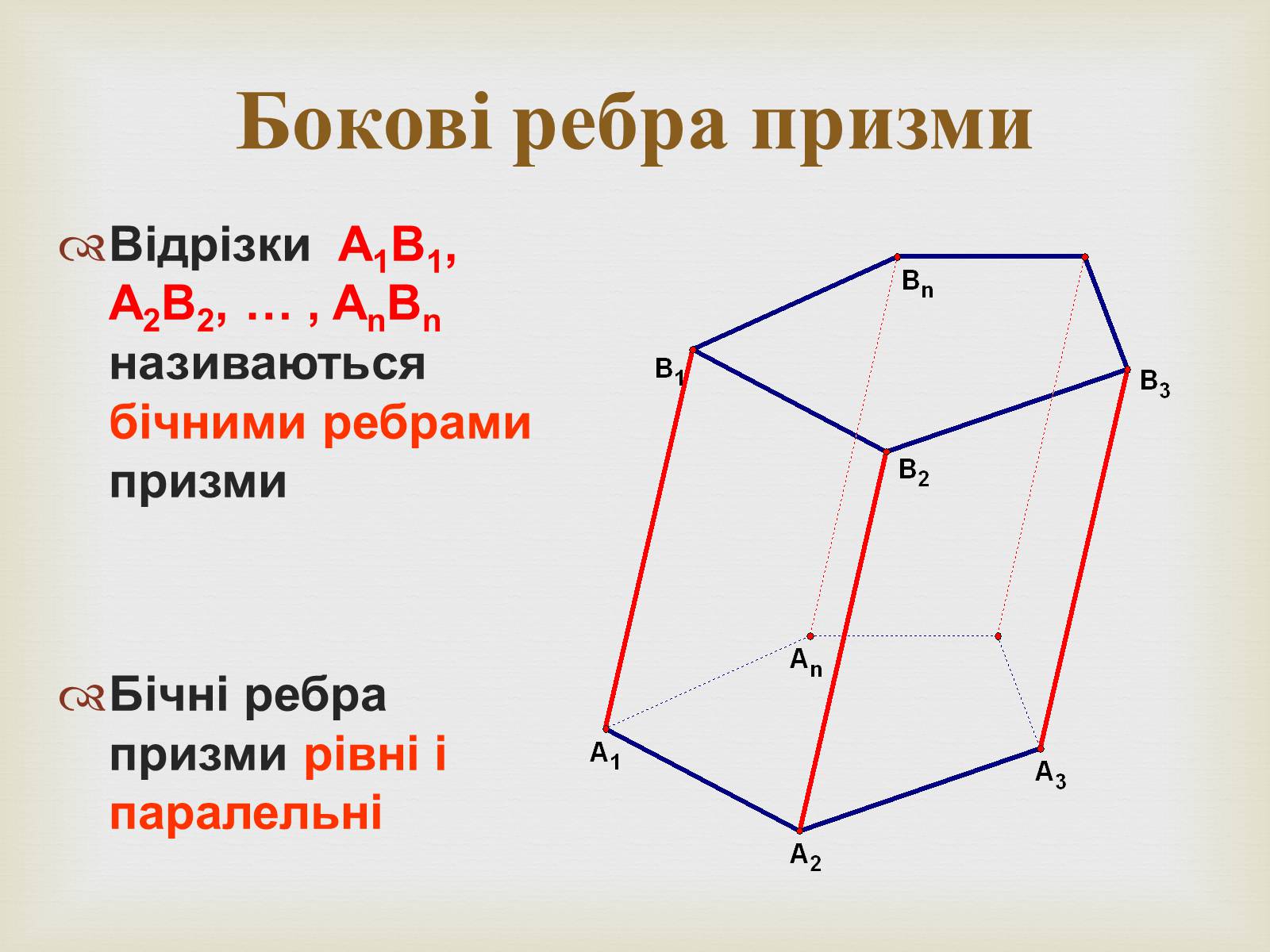
Бокові ребра призми
Відрізки A1B1, A2B2, … , AnBn називаються бічними ребрами призми
Бічні ребра призми рівні і паралельні
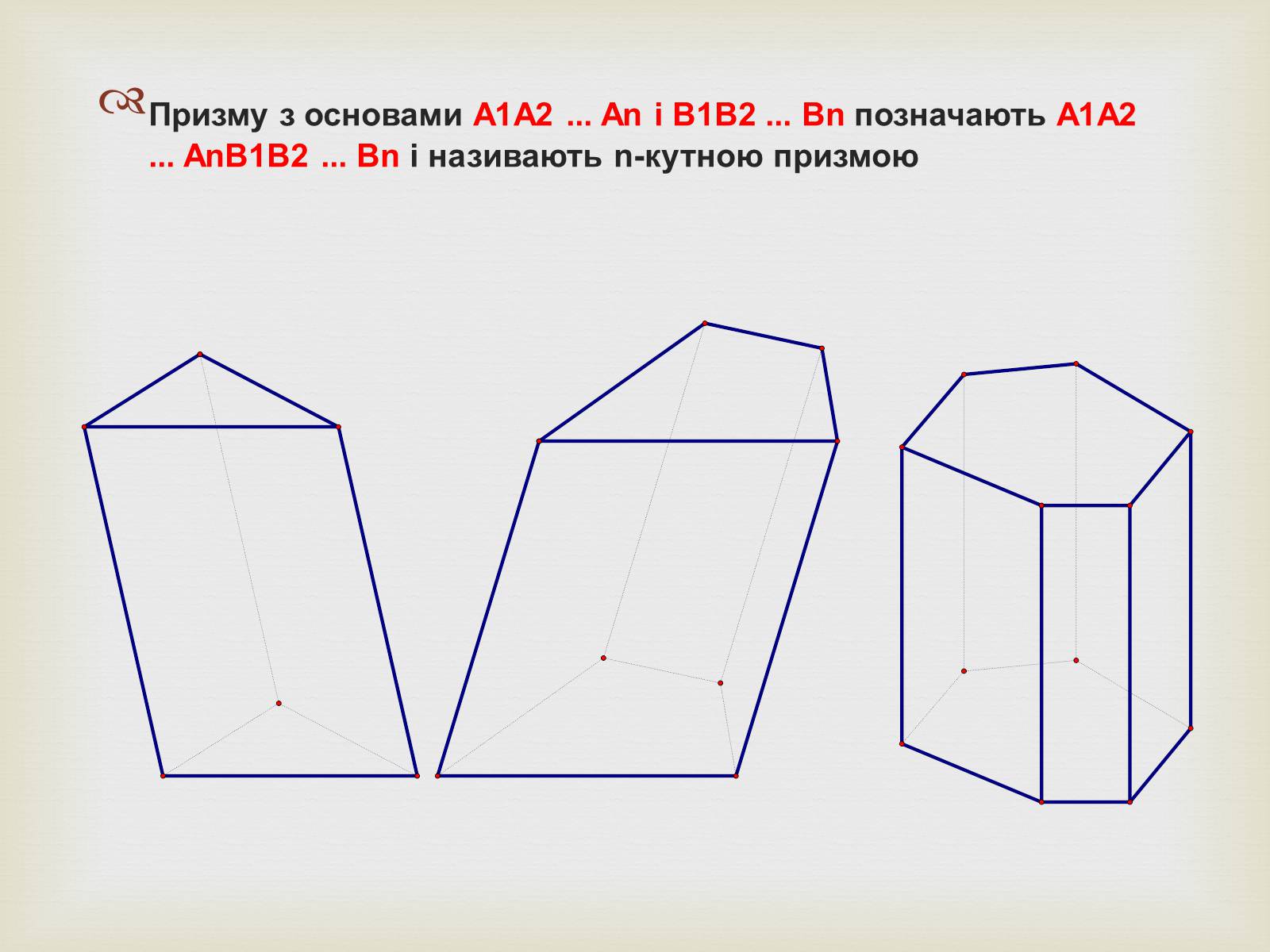
Призму з основами A1A2 ... An і B1B2 ... Bn позначають A1A2 ... AnB1B2 ... Bn і називають n-кутною призмою
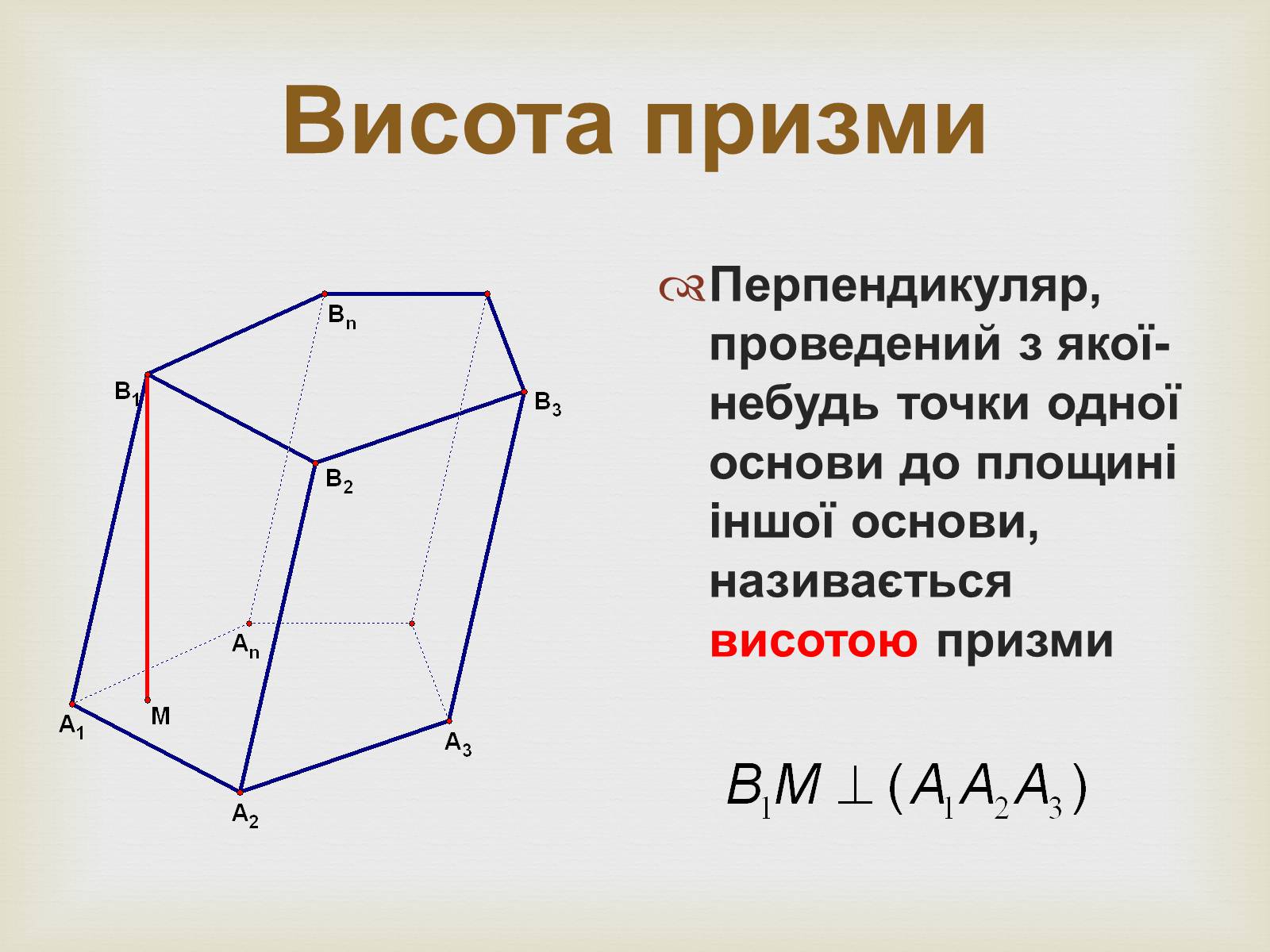
Висота призми
Перпендикуляр, проведений з якої-небудь точки одної основи до площині іншої основи, називається висотою призми

Пряма і похила призми
Якщо бічні ребра призми перпендикулярні до основи, то призма називається прямою,
в іншому випадку - похилою
Висота прямої призми дорівнює її бічному ребру

Правильна призма
Пряма призма називається правильною, якщо в її основі - правильні багатокутники
У правильної призми всі бічні грані - рівні прямокутники

Правильні призми
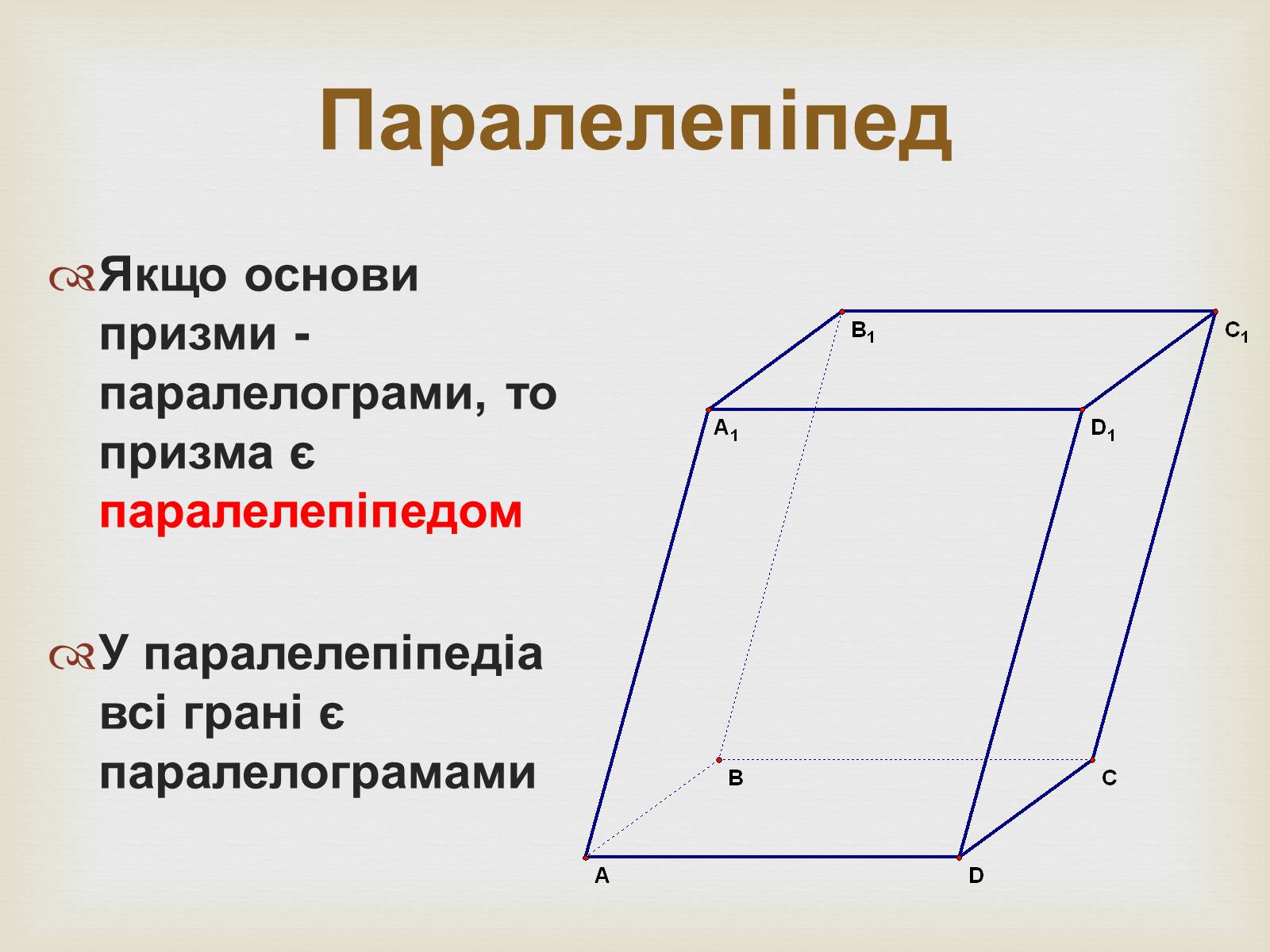
Паралелепіпед
Якщо основи призми - паралелограми, то призма є паралелепіпедом
У паралелепіпедіа всі грані є паралелограмами
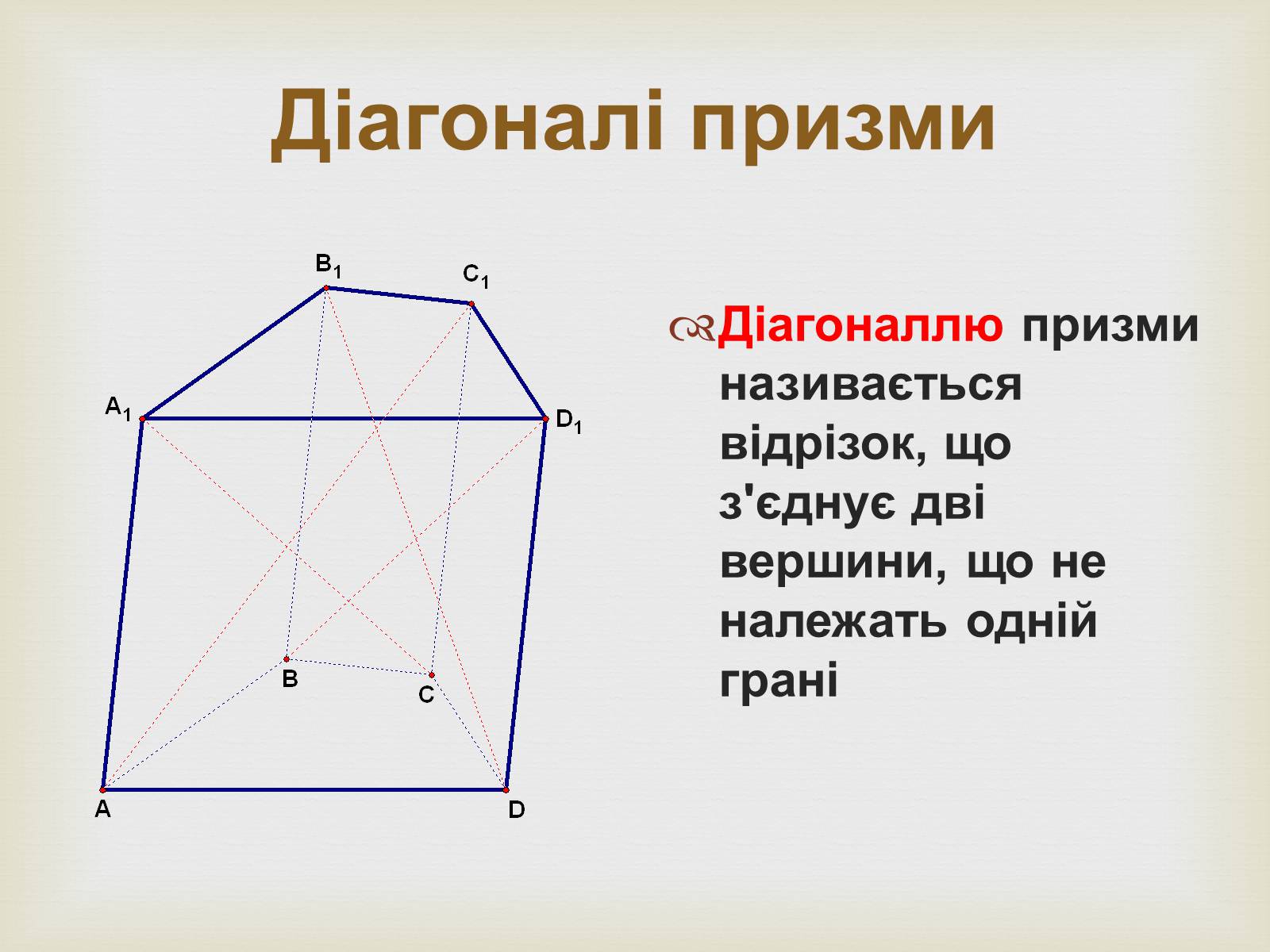
Діагоналі призми
Діагоналлю призми називається відрізок, що з'єднує дві вершини, що не належать одній грані
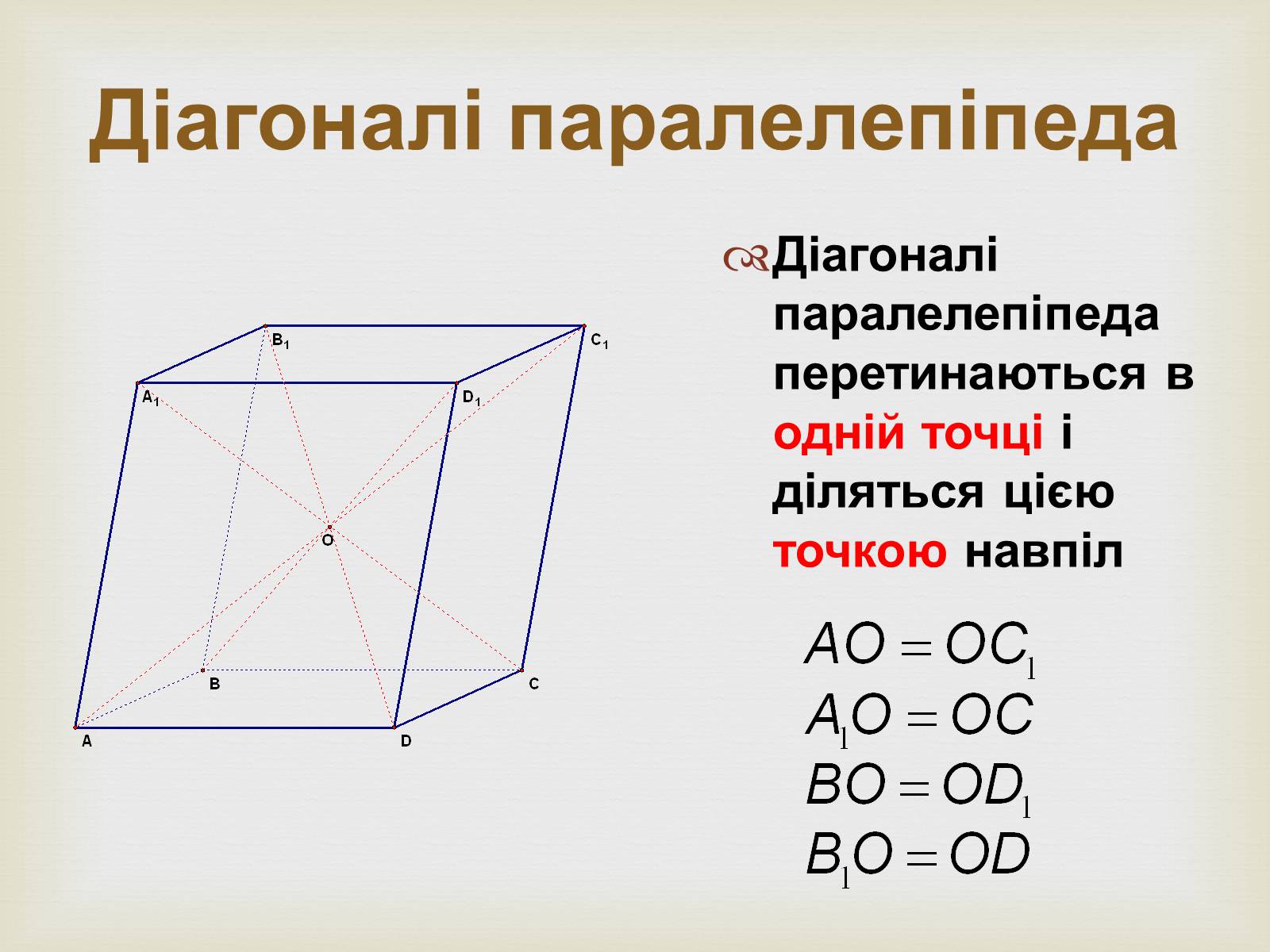
Діагоналі паралелепіпеда
Діагоналі паралелепіпеда перетинаються в одній точці і діляться цією точкою навпіл
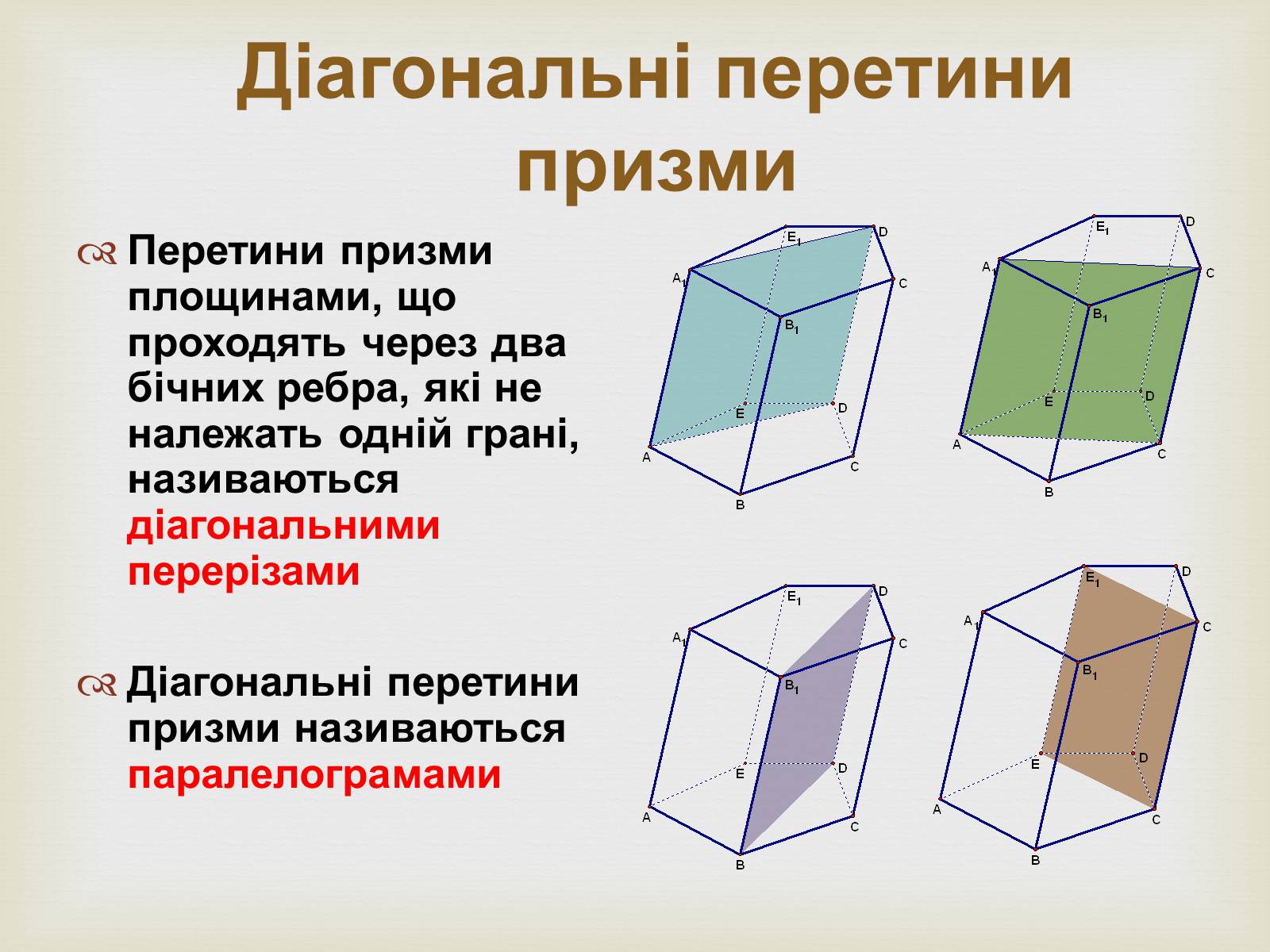
Діагональні перетини призми
Перетини призми площинами, що проходять через два бічних ребра, які не належать одній грані, називаються діагональними перерізами
Діагональні перетини призми називаються паралелограмами
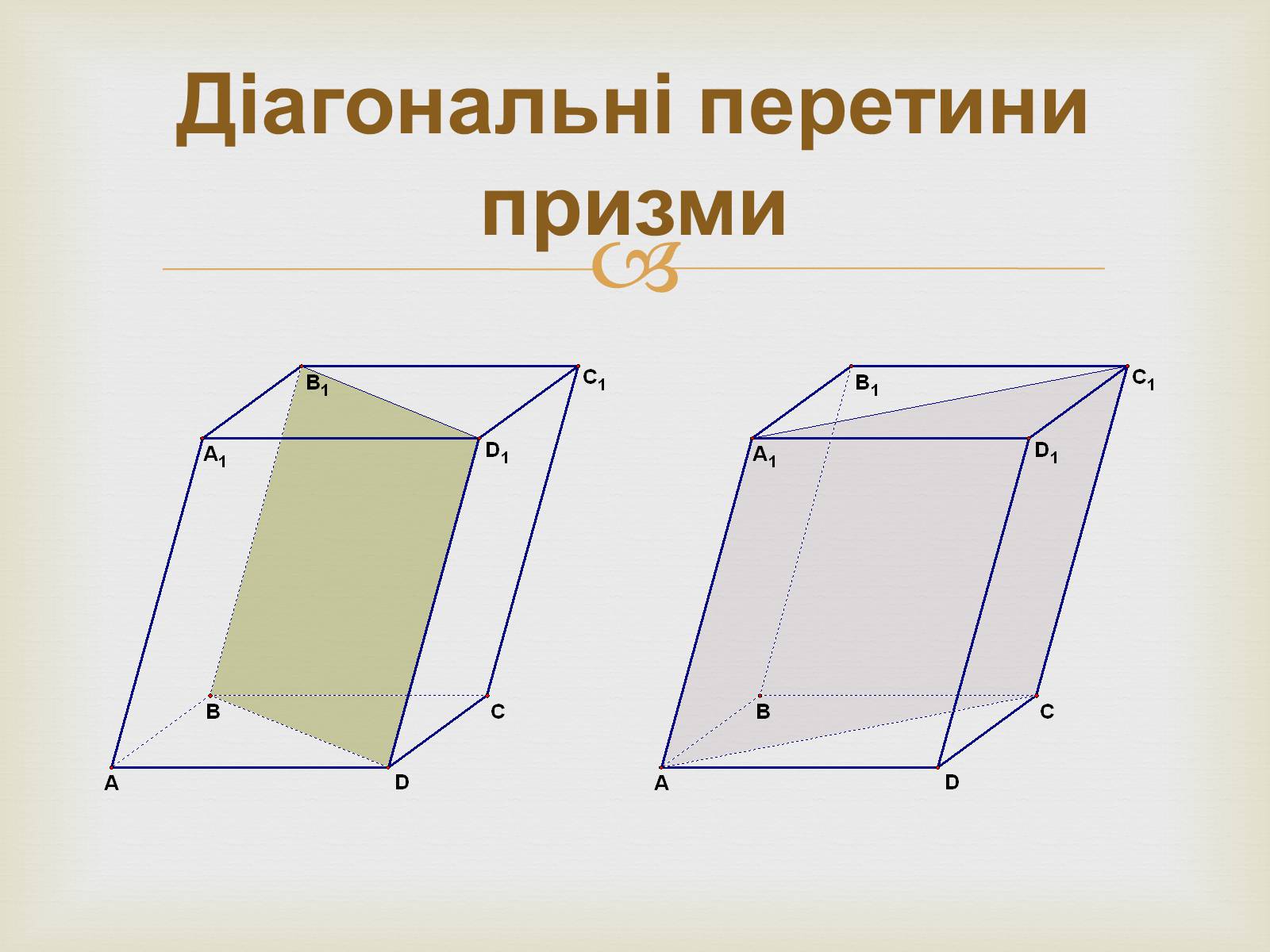
Діагональні перетини призми

Площею повної поверхні призми називається сума площ всіх її граней
Площею бічної поверхні призми називається сума площ її бічних граней
Площа поверхні призми

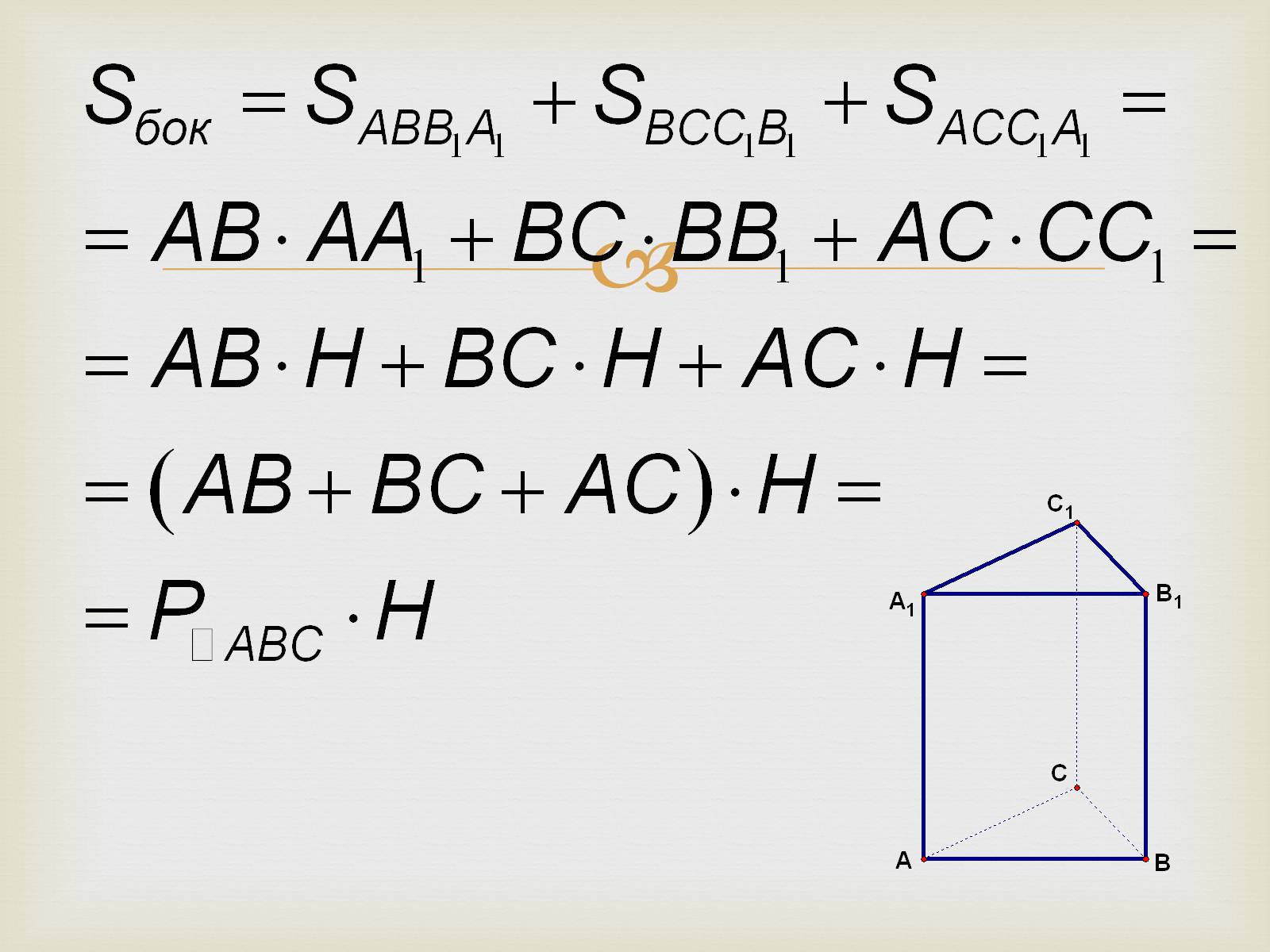
Теорема про площу бічної поверхні прямої призми
Теорема.
Площа бічної поверхні прямої призми дорівнює добутку периметра основи на висоту призми