Презентація на тему «Об’єми і площі поверхонь геометричних тіл»

Автор: Ананьєва Поліна
ГЕОМЕТРІЯ
11
Об'єми і площі поверхонь геометричних тіл
МІНІ-підручник
Об'єм та площа прямої призми і циліндра
Об'єм та площа піраміди
Об'єм та площа конуса
Об'єм та площа кулі

Зміст
Поняття об'єму
Об'єм та площа
прямої призми і циліндра
Об'єм та площа
прямої піраміди і зрізаної піраміди
Об'єм та площа
прямої конуса і зрізного конуса
Об'єм та площа
прямої кулі і їїчастин
Об'ємом геометричного тіла називається додатне число, яке характеризує частину простору, що займає геометричне тіло, і задовольняє таким умовам:

Формула для об 'єму прямокутного паралелепіпеда
Теорема
Об'єм прямокутного паралелепіпеда
дорівнює добутку трьох його вимірів,
тобто якщо а, b, с — лінійні виміри
прямокутного паралелепіпеда, то
його об'єм V обчислюється за формулою
V = аbс .

Циліндром називається тіло, утворене обертанням прямокутника навколо його сторони.
Циліндр

Призма – многогранник,
дві грані якого – рівні
n-кутники з
відповідно паралельними
сторонами, а всі інші
грані – паралелограми
Призма

Піраміда
P – вершина піраміди;
ABCD – основа піраміди;
∆PAB, ∆PBC, ∆PCD,
∆PDA – бічні грані;
PA, PB, PC, PD – бічні ребра;
AB, BC, CD, AD – ребра основи;
PO – висота, PO┴ABCD.
Піраміда – це многогранник, одна грань якого – довільний n-кутник, а всі інші – n граней трикутники, що мають спільну вершину.
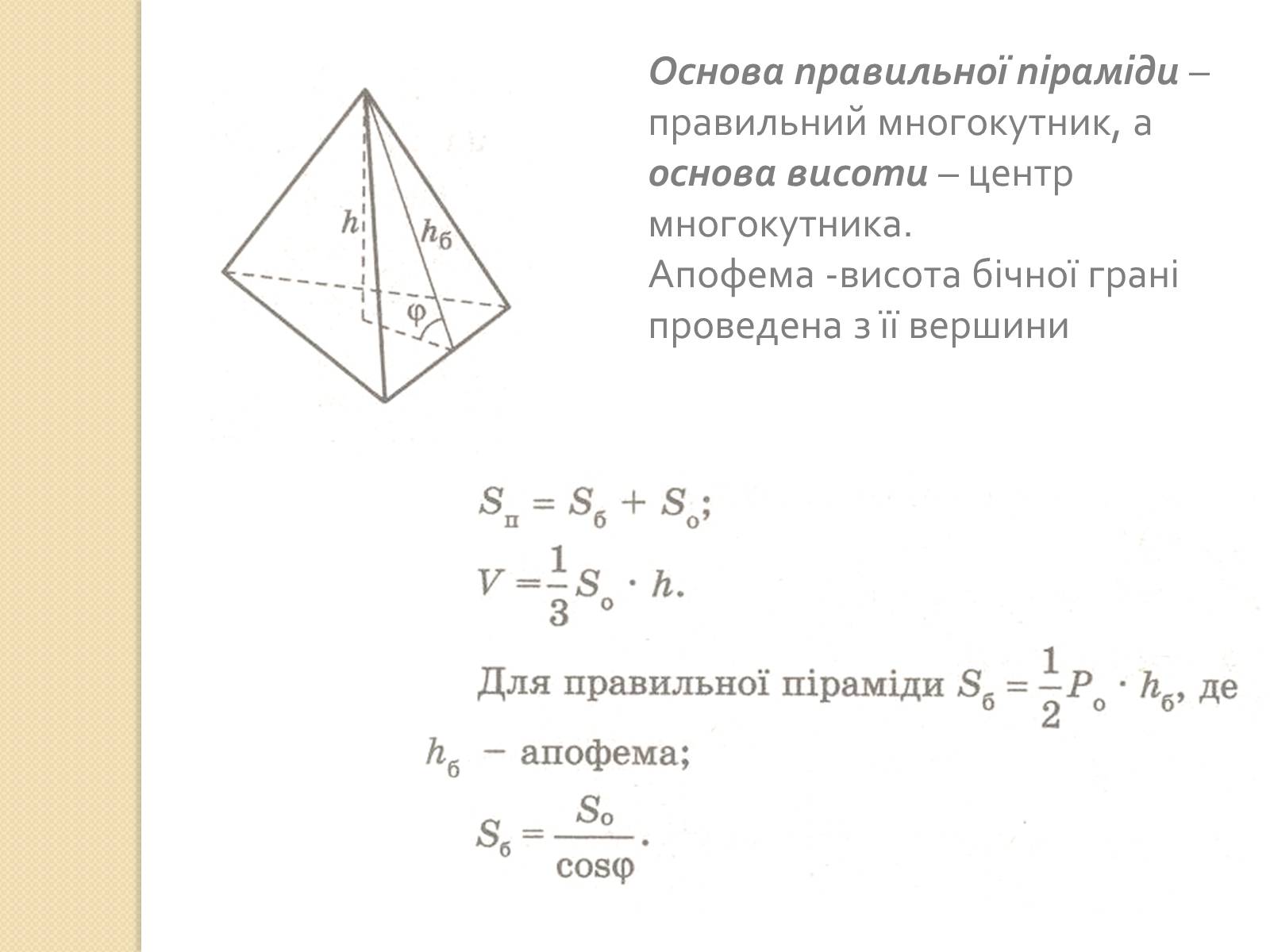
Основа правильної піраміди – правильний многокутник, а основа висоти – центр многокутника.
Апофема -висота бічної грані проведена з її вершини
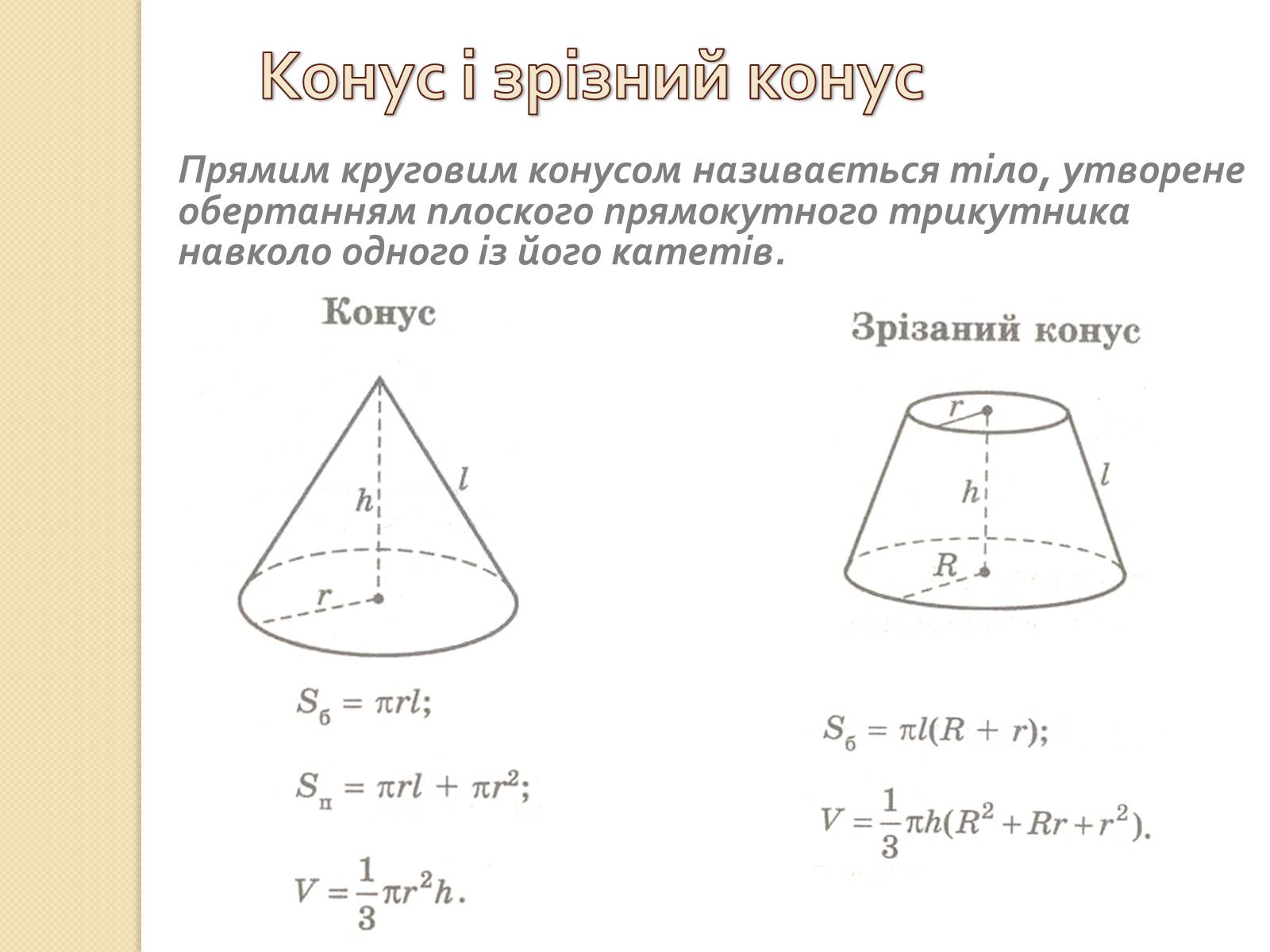
Конус і зрізний конус
Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів.
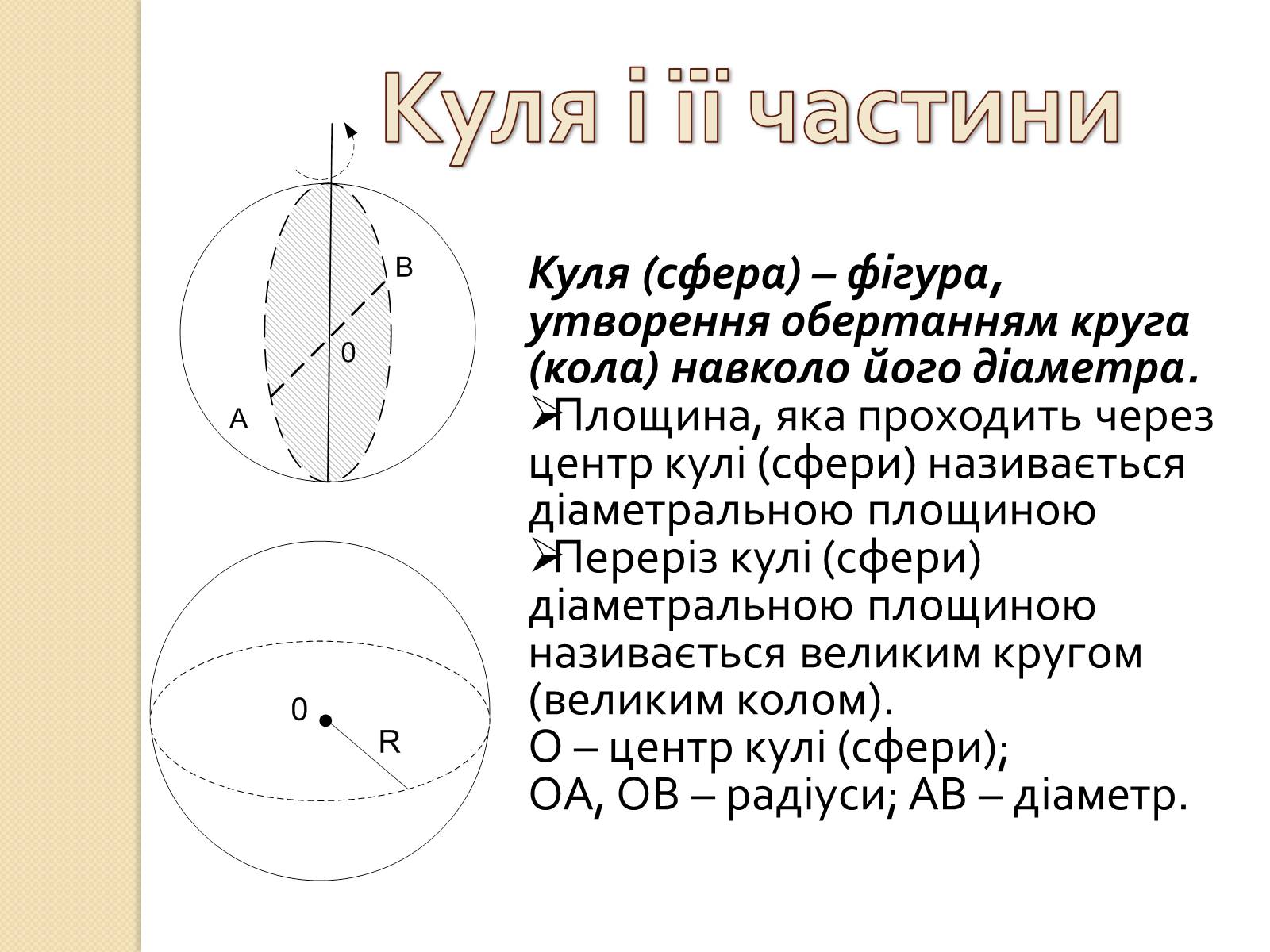
Куля і її частини
Куля (сфера) – фігура, утворення обертанням круга (кола) навколо його діаметра.
Площина, яка проходить через центр кулі (сфери) називається діаметральною площиною
Переріз кулі (сфери) діаметральною площиною називається великим кругом (великим колом).
О – центр кулі (сфери);
ОА, ОВ – радіуси; АВ – діаметр.
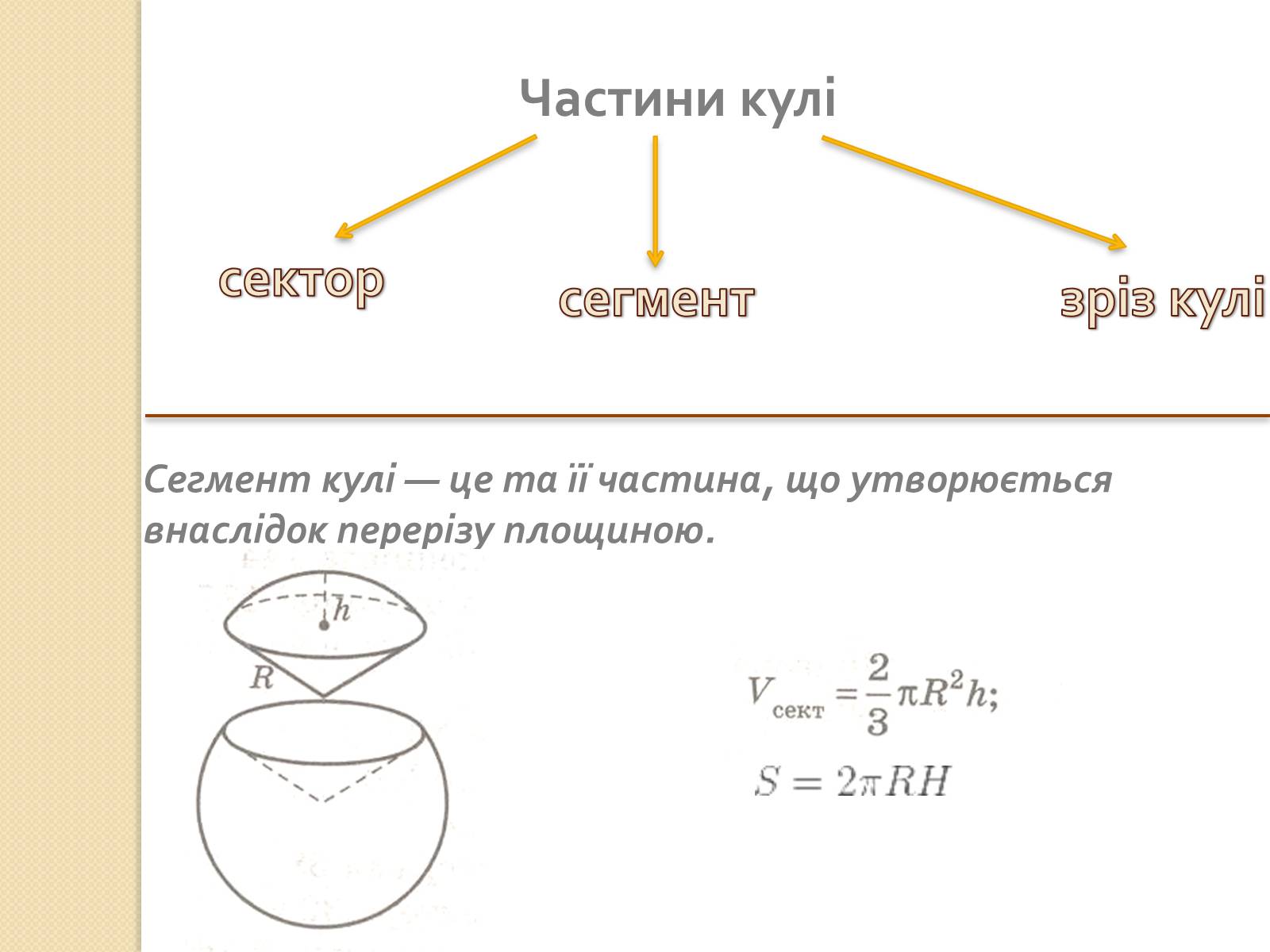
Частини кулі
Сегмент кулі — це та її частина, що утворюється внаслідок перерізу площиною.
сектор
сегмент
зріз кулі
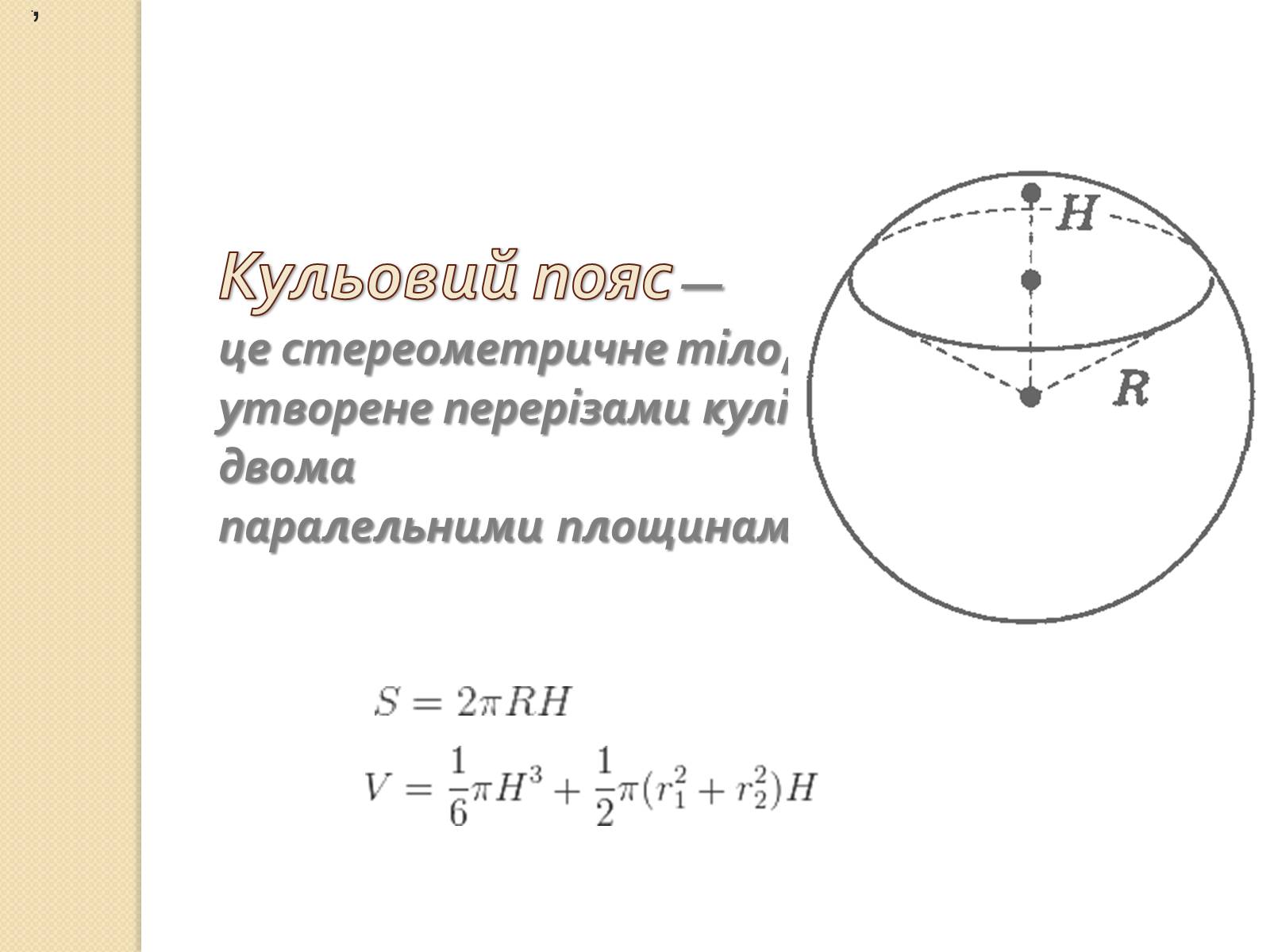
Кульовий пояс — це стереометричне тіло, утворене перерізами кулі двома паралельними площинами
,
.

Сектор складається з кульового сегмента та конуса, основа якого збігається з основою сегмента, а вершина — з центром кулі.
.
S=
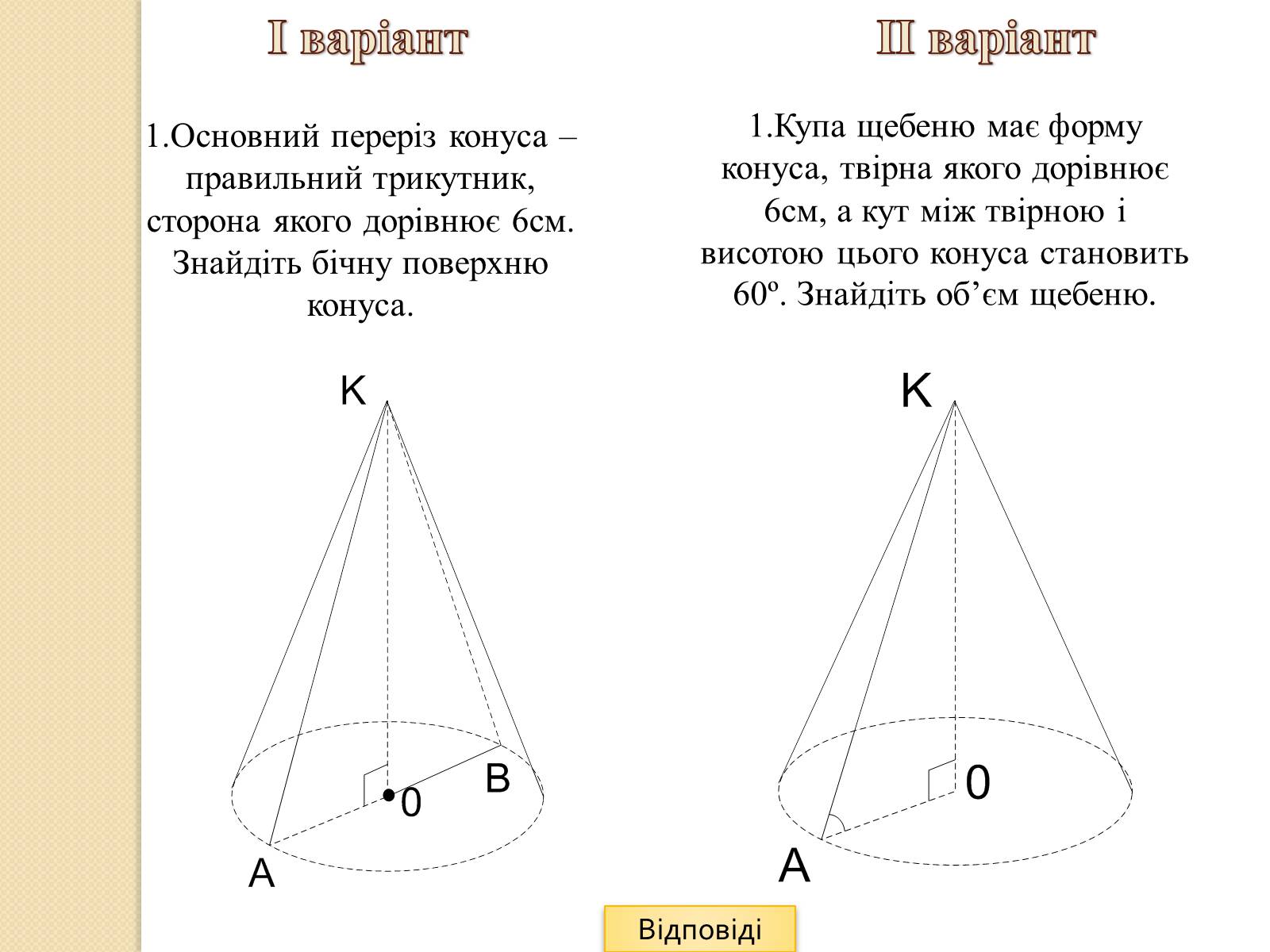
1.Основний переріз конуса – правильний трикутник, сторона якого дорівнює 6см. Знайдіть бічну поверхню конуса.
1.Купа щебеню має форму конуса, твірна якого дорівнює 6см, а кут між твірною і висотою цього конуса становить 60º. Знайдіть об'єм щебеню.
Відповіді
І варіант ІІ варіант
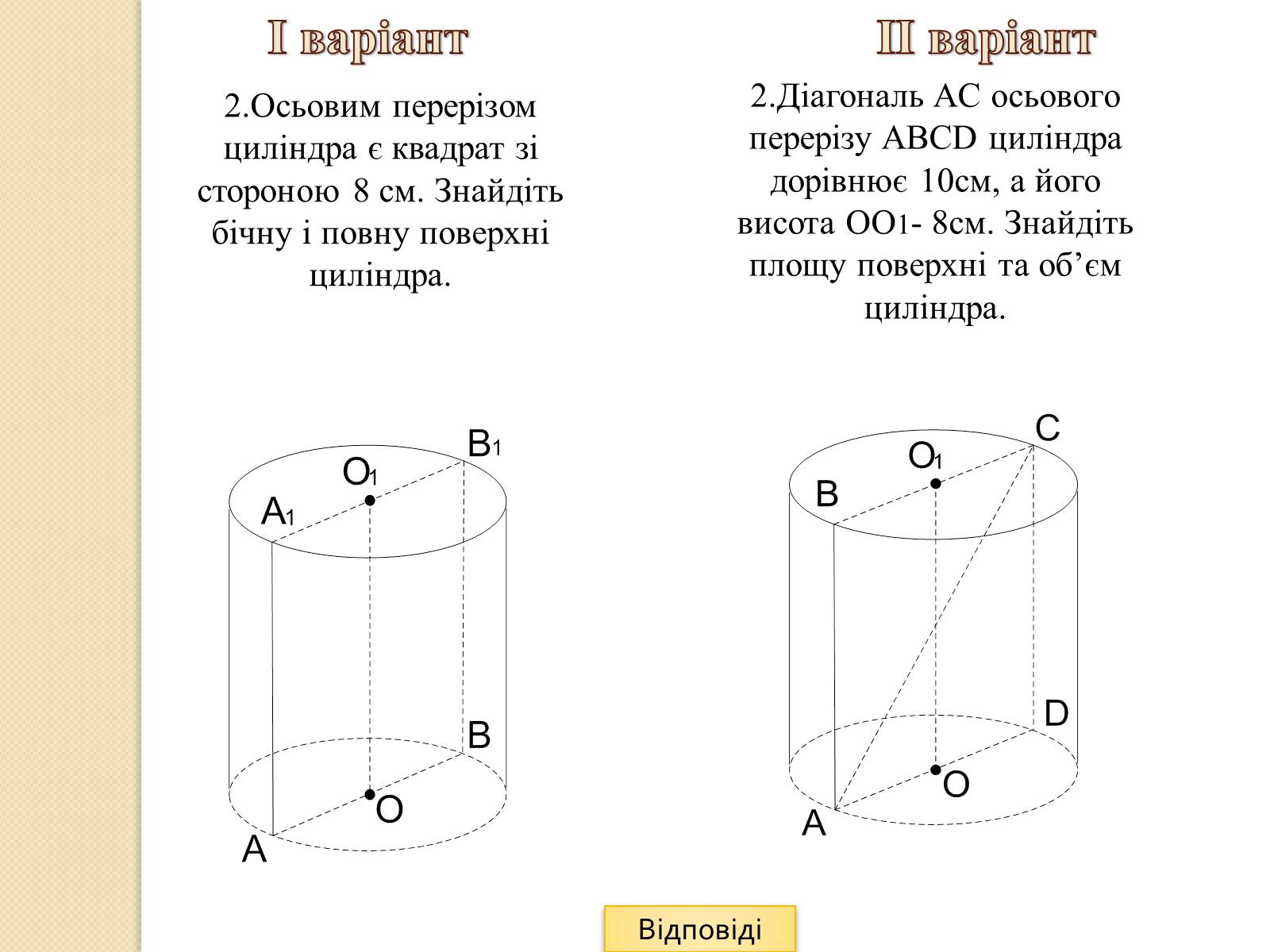
2.Діагональ AC осьового перерізу ABCD циліндра дорівнює 10см, а його висота ОО1- 8см. Знайдіть площу поверхні та об'єм циліндра.
2.Осьовим перерізом циліндра є квадрат зі стороною 8 см. Знайдіть бічну і повну поверхні циліндра.
Відповіді
І варіант ІІ варіант
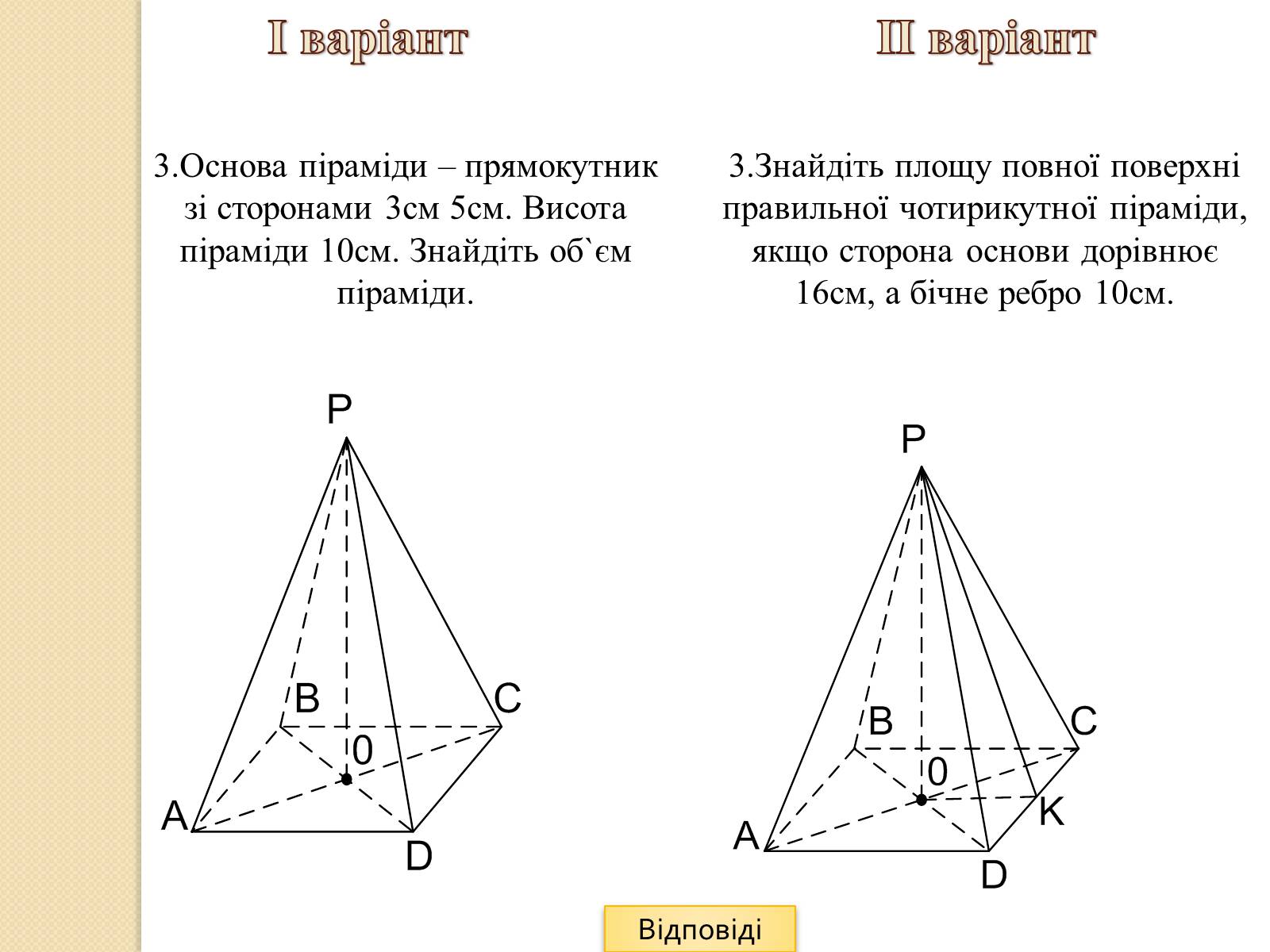
3.Основа піраміди – прямокутник зі сторонами 3см 5см. Висота піраміди 10см. Знайдіть об`єм піраміди.
3.Знайдіть площу повної поверхні правильної чотирикутної піраміди, якщо сторона основи дорівнює 16см, а бічне ребро 10см.
Відповіді
І варіант ІІ варіант
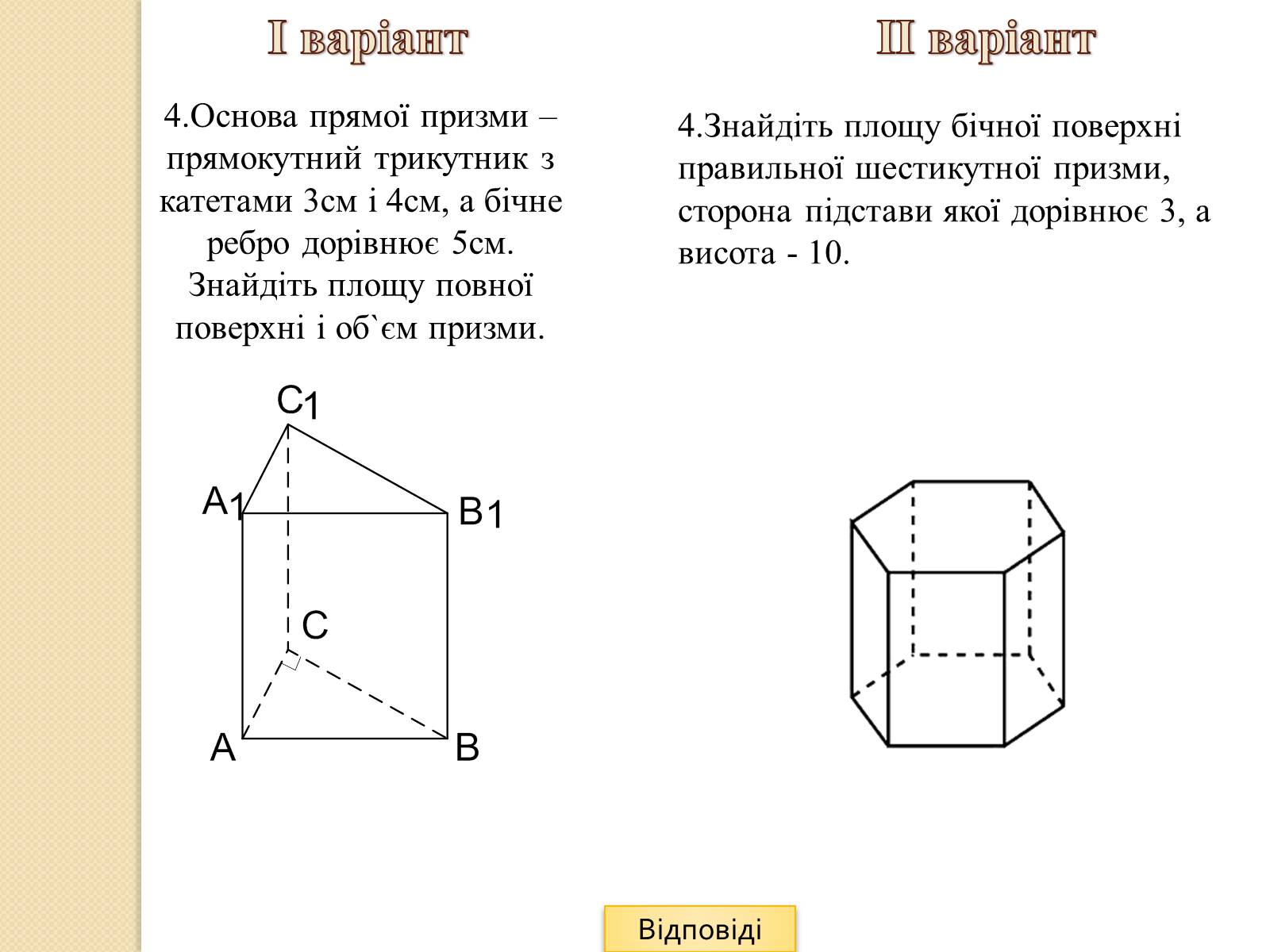
4.Основа прямої призми – прямокутний трикутник з катетами 3см і 4см, а бічне ребро дорівнює 5см. Знайдіть площу повної поверхні і об`єм призми.
4.Знайдіть площу бічної поверхні правильної шестикутної призми, сторона підстави якої дорівнює 3, а висота - 10.
Відповіді
І варіант ІІ варіант

Дано: конус, ΔАКВ – правильний АК=КВ=АВ=6см.
Знайти: Sбічн.
Розв'язання
Sбічн.=πRL; L=KB=6см.
ΔАКВ – правильний, то КО – висота і медіана АО=ОВ=3см, R=3см.
Sбічн.=πRL=π*3*6=18π (см²)
Відповідь: 18π см²
Дано: конус, АК – твірна,
АО – висота.
ےАКО=60º, АК=6см.
Знайти: Vкон.
Розв'язання
V=1/3 πR²H
ΔАКО – прямокутний, ےАКО=60º, то ےКАО=30º.
КО=1/2*6=3(см) (катет, що лежить проти кута 30º)
За теоремою Піфагора з ΔАКО КО=√АК² – АО²=√6²-3²=√27=3√3
V=1/3πR²H=1/3π*(3√3)²*3=27π(см³)
Відповідь: 27π см³
До завдань
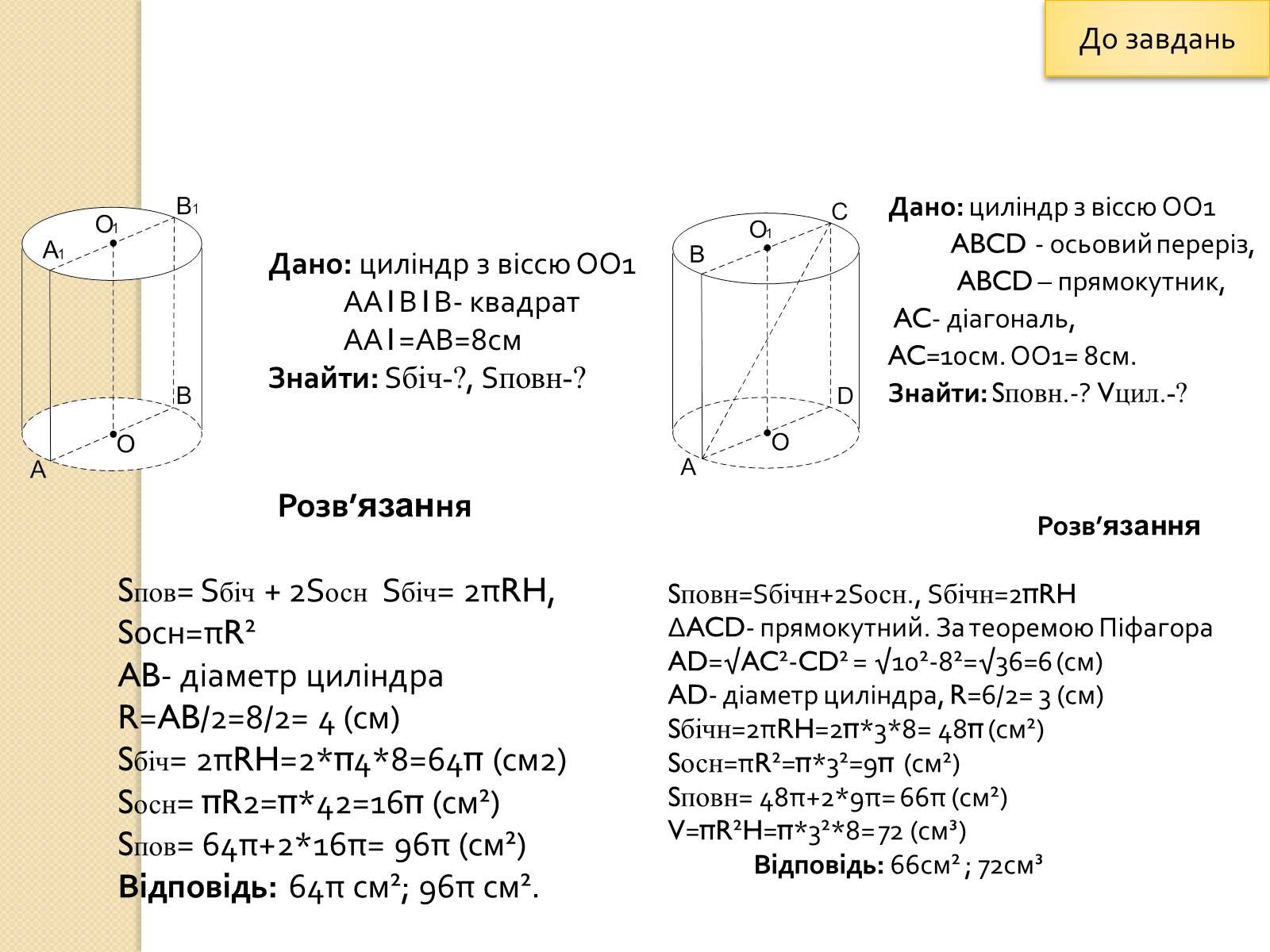
Дано: циліндр з віссю ОО1
АА1В1В- квадрат
АА1=АВ=8см
Знайти: Sбіч-?, Sповн-?
Розв'язання
Sпов= Sбіч + 2Sосн Sбіч= 2πRH, Sосн=πR²
AB- діаметр циліндра R=AB/2=8/2= 4 (см)
Sбіч= 2πRH=2*π4*8=64π (см2)
Sосн= πR2=π*42=16π (см²)
Sпов= 64π+2*16π= 96π (см²)
Відповідь: 64π см²; 96π см².
Дано: циліндр з віссю ОО1
ABCD - осьовий переріз,
ABCD – прямокутник,
AC- діагональ,
AC=10см. ОО1= 8см.
Знайти: Sповн.-? Vцил.-?
Розв'язання
Sповн=Sбічн+2Sосн., Sбічн=2πRH
∆ACD- прямокутний. За теоремою Піфагора
AD=√AC²-CD² = √10²-8²=√36=6 (см)
AD- діаметр циліндра, R=6/2= 3 (см)
Sбічн=2πRH=2π*3*8= 48π (см²)
Sосн=πR²=π*3²=9π (см²)
Sповн= 48π+2*9π= 66π (см²)
V=πR²H=π*3²*8= 72 (см³)
Відповідь: 66см² ; 72см³
До завдань
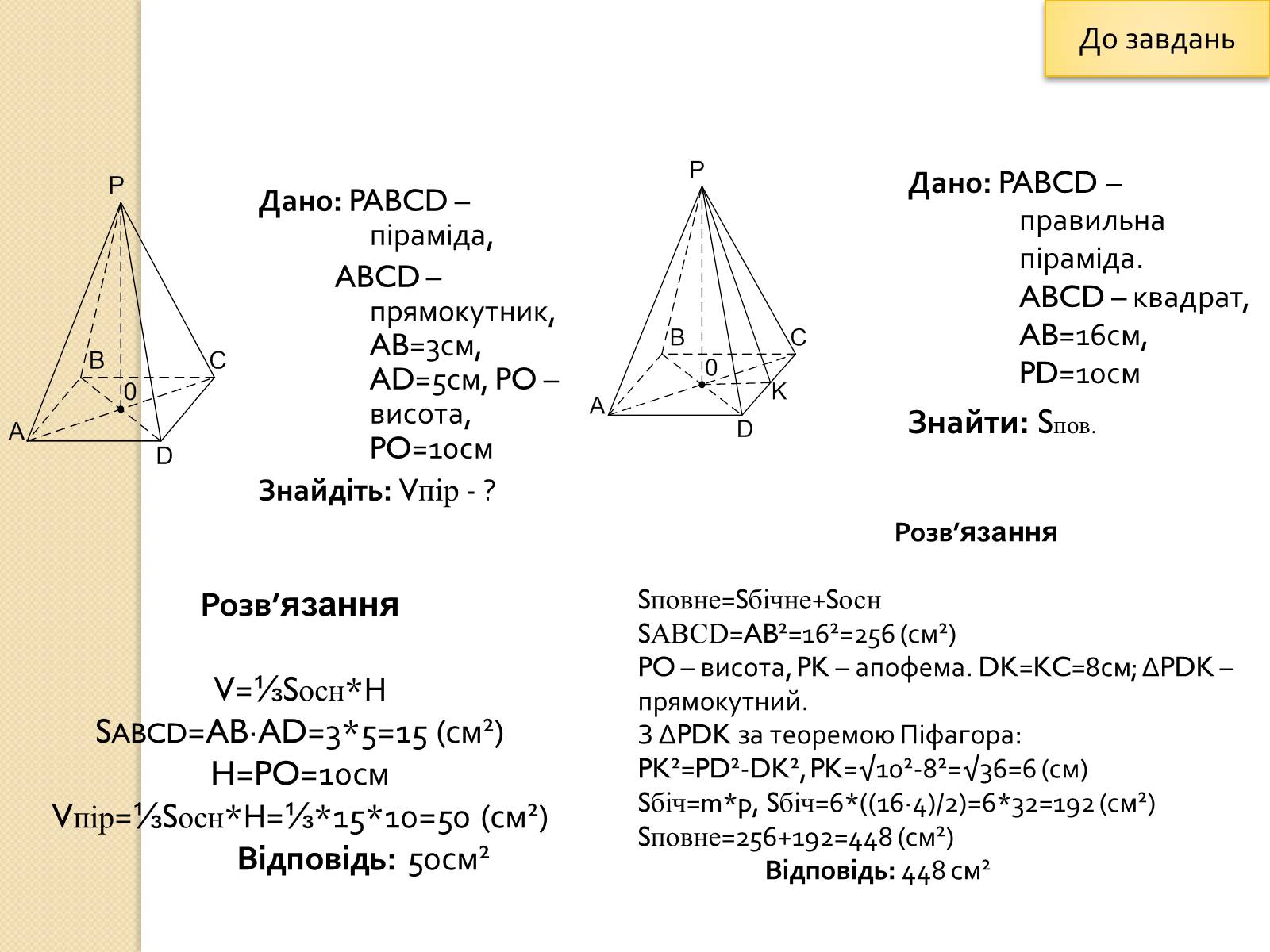
Дано: PABCD – піраміда,
ABCD – прямокутник, AB=3см, AD=5см, PO – висота, PO=10см
Знайдіть: Vпір - ?
Розв'язання
V=⅓Sосн*Н
SABCD=AB∙AD=3*5=15 (см²)
H=PO=10см
Vпір=⅓Sосн*Н=⅓*15*10=50 (см²)
Відповідь: 50см²
Дано: PABCD – правильна піраміда. ABCD – квадрат, AB=16см, PD=10см
Знайти: Sпов.
Розв'язання
Sповне=Sбічне+Sосн
SABCD=AB²=16²=256 (см²)
PO – висота, PK – апофема. DK=KC=8см; ∆PDK – прямокутний.
З ∆PDK за теоремою Піфагора:
PK²=PD²-DK², PK=√10²-8²=√36=6 (см)
Sбіч=m*p, Sбіч=6*((16∙4)/2)=6*32=192 (см²)
Sповне=256+192=448 (см²)
Відповідь: 448 см²
До завдань
Дано: ABCA1B1C1 – пряма призма
∆ACB – прямокутний, кут C=90º
AC=3см, CB=4см, АА1=5см
Знайти: Sповн; Vпризми - ?
Розв'язання
З ∆ACB за теоремою Піфагора AB²=AC²+CB²;
AB=√3²+4²=5 (см)
Sбічн=P*h=(3+4+5)*5=60 (см²)
Sосн=1/2AC*CB=1/2*3*4=6 (см²)
Sповн=60+2*6=72 (см²)
Vпризми= Sосн∙h=6*5=30 (см³)
Відповідь: 72см², 30см³
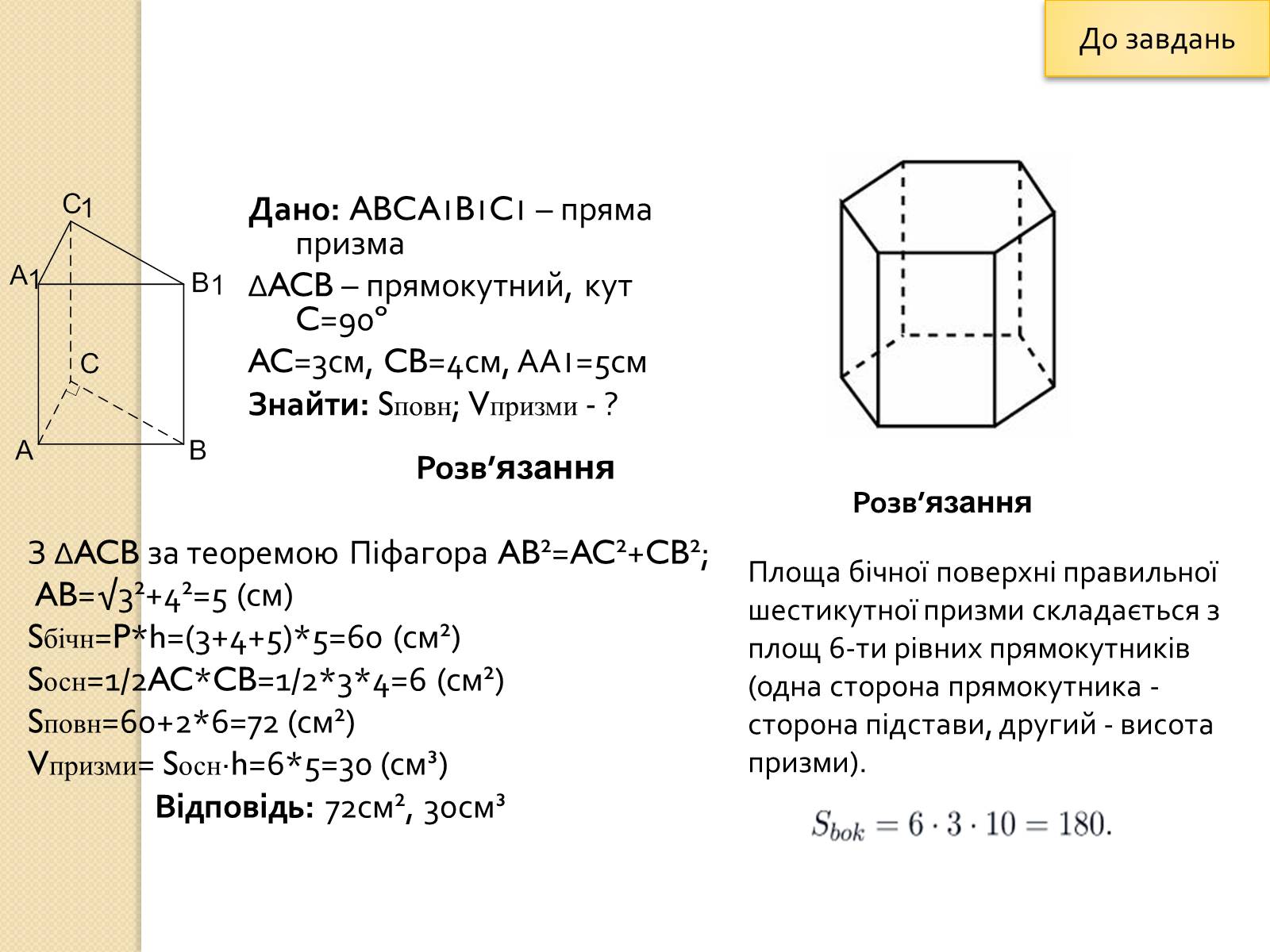
Розв'язання
Площа бічної поверхні правильної шестикутної призми складається з площ 6-ти рівних прямокутників (одна сторона прямокутника - сторона підстави, другий - висота призми).
До завдань