Презентація на тему «Геометричні перетворення» (варіант 1)

Геометричні перетворення
Виконали:Павлова Марина і Перевертайло Олександра
учениці 9-ІТ класу

Перетворення
Означення:
Перетворенням фігури F фігуру F' називається така відповідність, при якій:
1) кожній точці фігури F відповідає єдина точка фігури F';
2)кожній точці фігури F' відповідає деяка точка фігури F;
3)різним точкам фігури F відповідають різні точки фігури F';
Фігура F' називається образом фігури F для даного перетворення.

Симетрія – це узгодженість розмірів, однаковість у розміщенні частин.
Види симетрії:
1)Центральна симетрія
2)Осьова симетрія
3)Паралельне перенесення
4)Поворот
5) Гомотетія

А
А`
B
B`
O
C
C`
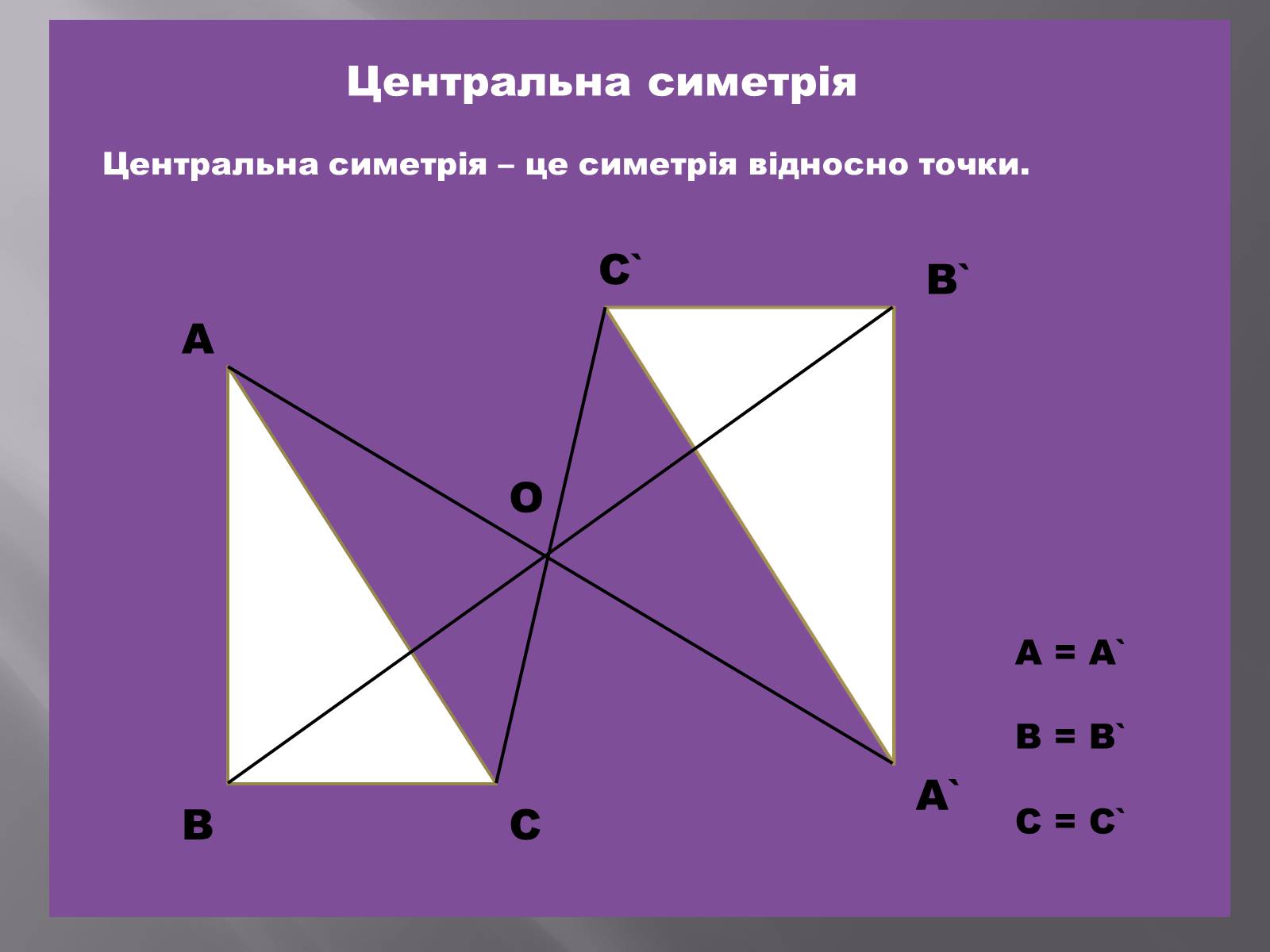
Центральна симетрія
А = А`
B = B`
C = C`
Центральна симетрія – це симетрія відносно точки.

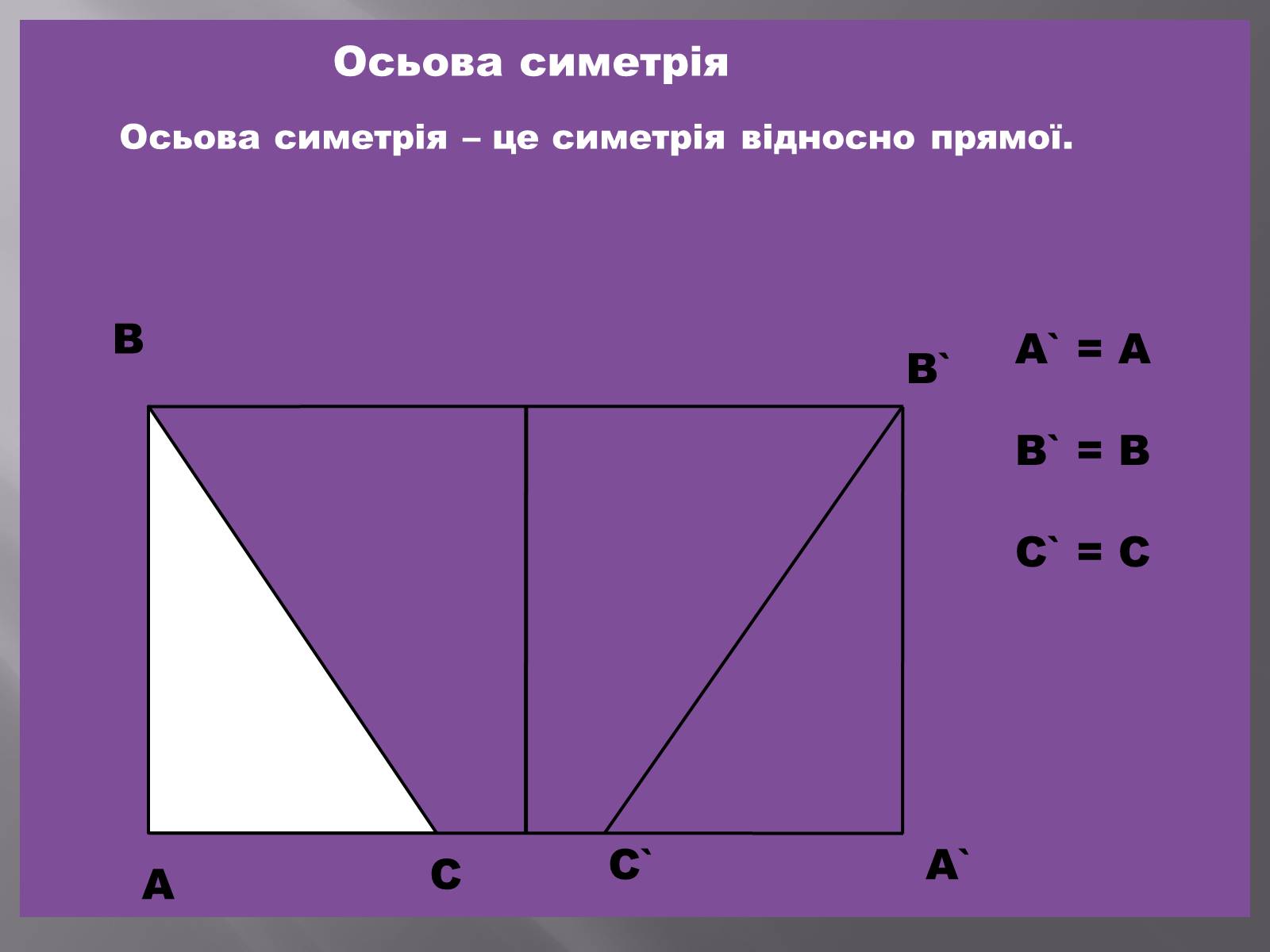
Осьова симетрія
Осьова симетрія – це симетрія відносно прямої.
А
В
С
С`
B`
A`
A` = A
B` = B
C` = C

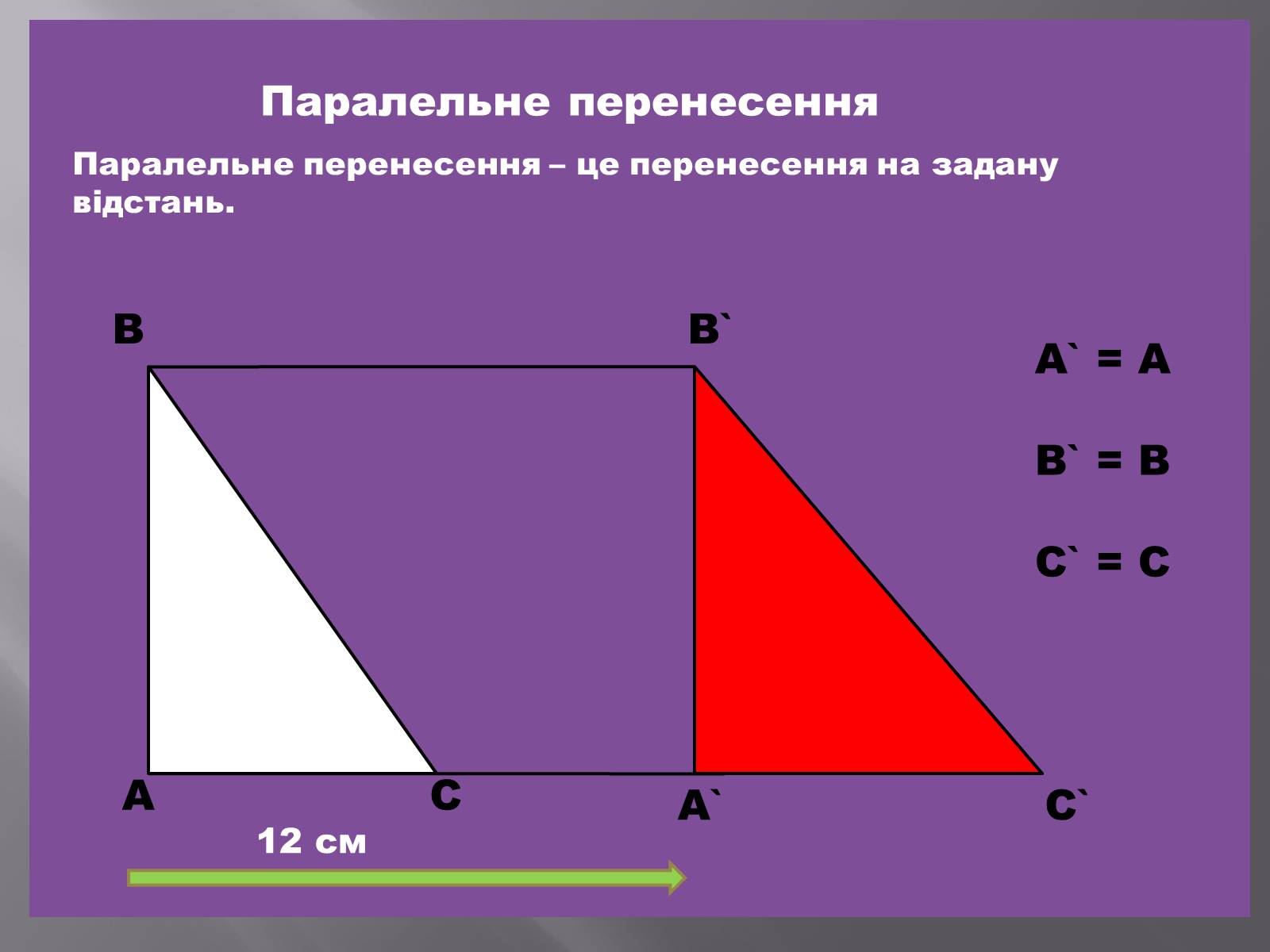
Паралельне перенесення
Паралельне перенесення – це перенесення на задану відстань.
12 см
А
В
С
A`
B`
C`
A` = A
B` = B
C` = C

A
B
C
O
C`
A`
B`
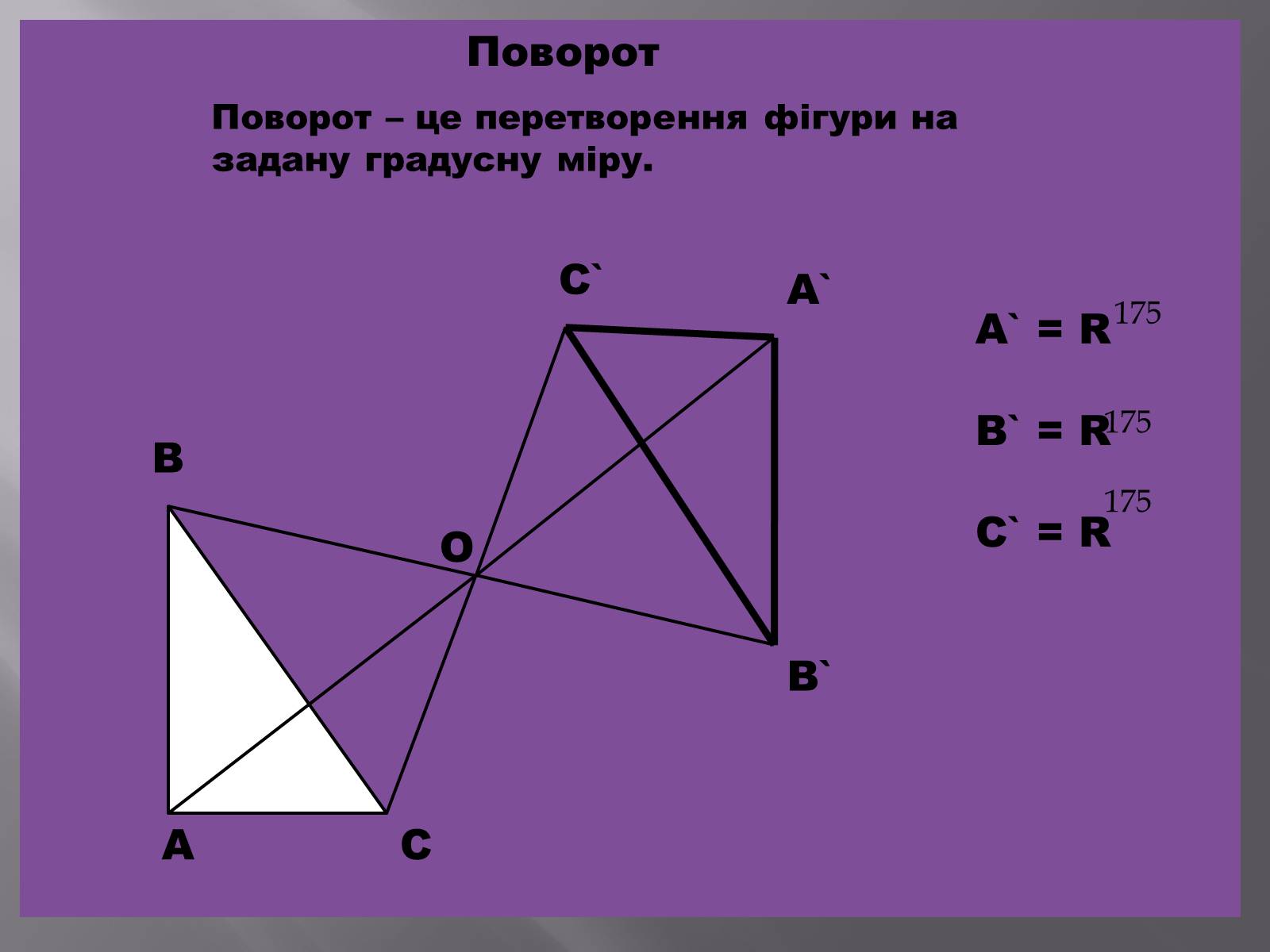
Поворот
Поворот – це перетворення фігури на задану градусну міру.
A` = R
B` = R
C` = R
175
175
175

A
B
C
B`
C`
A`
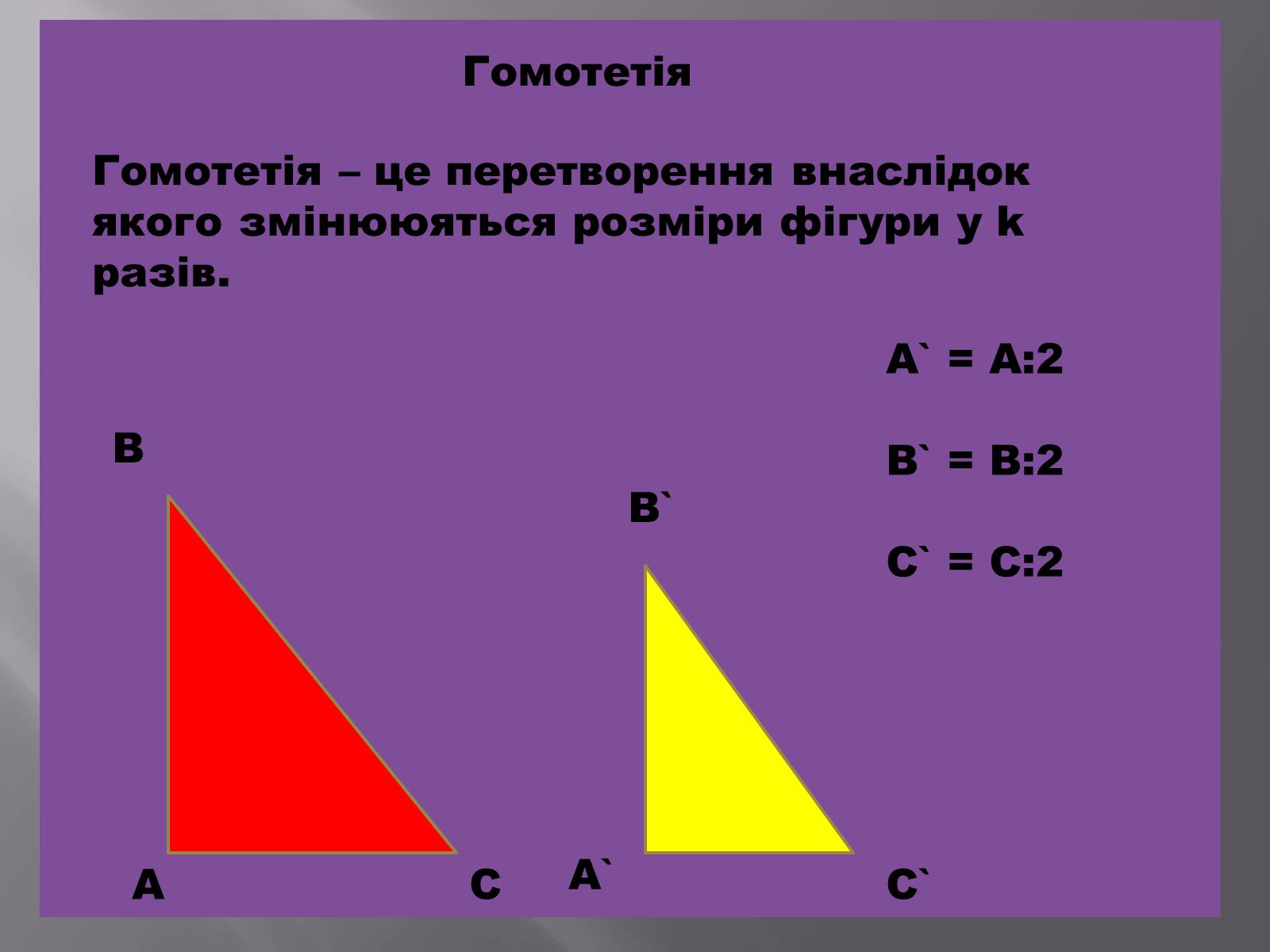
Гомотетія
Гомотетія – це перетворення внаслідок якого змінююяться розміри фігури у k разів.
A` = A:2
B` = B:2
C` = C:2

Приклади центральної симетрії

Приклади осьової симетрії

Приклади паралельного перенесення

Приклади повороту

Приклади гомотетії

И все)