Презентація на тему «Проценты» (варіант 1)

Исследовательская работа по теме «ПРОЦЕНТЫ»

ПЛАН
Введение
1. Из истории происхождения процентов
2. Решение задач на проценты разными способами
3. Решение задач по формуле сложных процентов
4. Решение задач на смеси и сплавы.
5. Применение процентов в жизни
Заключение
Список литературы

Почему я выбрал тему «Проценты»?
Проценты - это одна из сложнейших тем математики, и очень многие учащиеся затрудняются или вообще не умеют решать задачи на проценты. А понимание процентов и умение производить процентные расчёты необходимы для каждого человека. Прикладное значение этой темы очень велико и затрагивает финансовую, экономическую, демографическую и другие сферы нашей жизни. Изучение процента продиктовано самой жизнью. Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни. Немецкий физик 18-го столетия Лихтенберг сказал: « То, что вы были принуждены открыть сами, оставляет в вашем уме дорожку, которой вы сможете снова воспользоваться, когда в том возникнет необходимость». Поэтому я решил и сделал подборку задач из ГИА - 9 классов, из ЕГЭ - 11 классов на банковские проценты, где применяется формула сложных процентов.

Цель исследовательской работы
· Расширение знаний о применении процентных вычислений в задачах и из разных сфер жизни человека.

Задачи:
· Познакомиться с историей возникновения процентов;
· Решать задачи на проценты разными способами;
· Сделать подборку задач из ГИА - 9 кл., ЕГЭ -11кл., решаемые по формуле сложных процентов;
· Поработать в текстовом редакторе;
· Поработать с ресурсами Internet;
· Получить опыт публичного выступления.

История создания процентов.
В Европе в средние века расширилась торговля и, следовательно, особое внимание обращалось на умение вычислять проценты. Тогда приходилось рассчитывать не только проценты, но и проценты с процентов (сложные проценты). Часто конторы и предприятия для облегчения расчетов разрабатывали особые таблицы вычисления процентов. Эти таблицы держались в тайне, составляли коммерческий секрет фирмы. Впервые таблицы были опубликованы в 1584 году Симоном Стевином

Решение задач на проценты разными способами
Задачи с процентами можно решить разными способами:
уравнением;
составлением таблицы;
применяя пропорцию;
по действиям;
используя правила.

Решение задач на сложные проценты
Сложным процентом называется сумма дохода, которая образуется в результате инвестирования денег при условии, что сумма начисленного простого процента не выплачивается в конце каждого периода, а присоединяется к сумме основного вклада и в следующем платежном периоде сама приносит доход .
Сложные проценты - это проценты, полученные на начисленные проценты

Формула сложного процента
х(1+ 0,01а)
где х - начальный вклад, сумма.
а - процент(ы) годовых
n- время размещения вклада в банке
х(1- 0,01а)
периодическое увеличение некоторой величины
на одно и то же число процентов
периодическое уменьшение некоторой величины
на одно и то же число процентов.

Решение задач
Задача 1:
Вкладчик открыл счет в банке, внеся 2000 рублей на вклад, годовой доход по которому составляет 12%, и решил в течение шести лет не брать процентные начисления. Какая сумма будет лежать на счете через шесть лет?

Решим эту задачу по формуле сложных
процентов.
первоначальный вклад - 2000
процент годовых - 12
n - 6 лет, значит
2000(1 + 0,12) = 2000*1,126 = 2000*1,973823 = 3947,65
ОТВЕТ: через 6 лет на счете будет лежать сумма
в виде 3947 руб. и 65 коп..

Задача 2:
После двух последовательных снижений цен на одно и то же число процентов стоимость товара с 400 рублей снизилась до 324 рублей. На сколько процентов стоимость товара снижалась каждый раз?

Решение:
400*(1-0,01а)=324
20(1 - 0,01а) = 18
1 - 0,01а = 0,9
а = 10
ОТВЕТ: стоимость товара каждый раз
снижалась на 10%

Задача №3
В соответствии с договором фирма с целью компенсации потерь от инфляции была обязана в начале каждого квартала (3 месяца) повышать сотруднику зарплату на 2%. Однако в связи с финансовыми затруднениями она смогла повышать ему зарплату только раз в полгода (в начале следующего полугодия). На сколько % фирма должна повышать зарплату каждые полгода, чтобы первого января следующего года зарплата сотрудника была равна той, которую он получил бы в режиме повышения, предусмотренной договором?

Решение:
Для решения составим таблицу
Через какое время повышается
на сколько % повышается
Какая зарплата будет
Через каждые 3 месяца
2%
х(1+0,02)4
Через каждые полгода
а%
х(1+0,01а)2

По таблице составим уравнение:
х(1+0,02) = х(1+0,01а)²
(1+0,02)² = (1+0,01а)
1+0,04+0,0004=1+0,01а
0,0404=0,01а
а = 4,04%
ОТВЕТ: через каждый полгода зарплату сотрудникам
надо поднимать на 4,04%

Решение задач на смеси и сплавы.
Задача 1.
При смешивании 5%-ного раствора кислоты с 40% -ным раствором кислоты получили 140г 30%-ного раствора. Сколько граммов каждого раствора было для этого взято?

Рассмотрим старинный способ решения этой задачи.
Друг под другом пишутся содержания кислот имеющихся растворов, слева от них и
примерно посередине – содержание кислоты в растворе, который должен получиться
после смешивания. Соединив написанные числа чёрточками получим такую схеме:
30
5
40
Рассмотрим пары 30 и 5, 30 и 40. В каждой паре из большего числа вычтем меньшее и результат запишем в конце соответствующей чёрточки . Получится такая схема:
10
30
5
40 25
Из неё делается заключение, что 5%-ного раствора следует взять 10 частей,
а 40% - ого 25 частей, т.е. для получения 140г. 30% - ого раствора нужно взять
5% - ого раствора 40г., а 40% - ого - 100г .(10+25=35частей всего, 140:35=4г-вес одной
части, 4×10=40г, 4×25=100г.)

Задача 2.
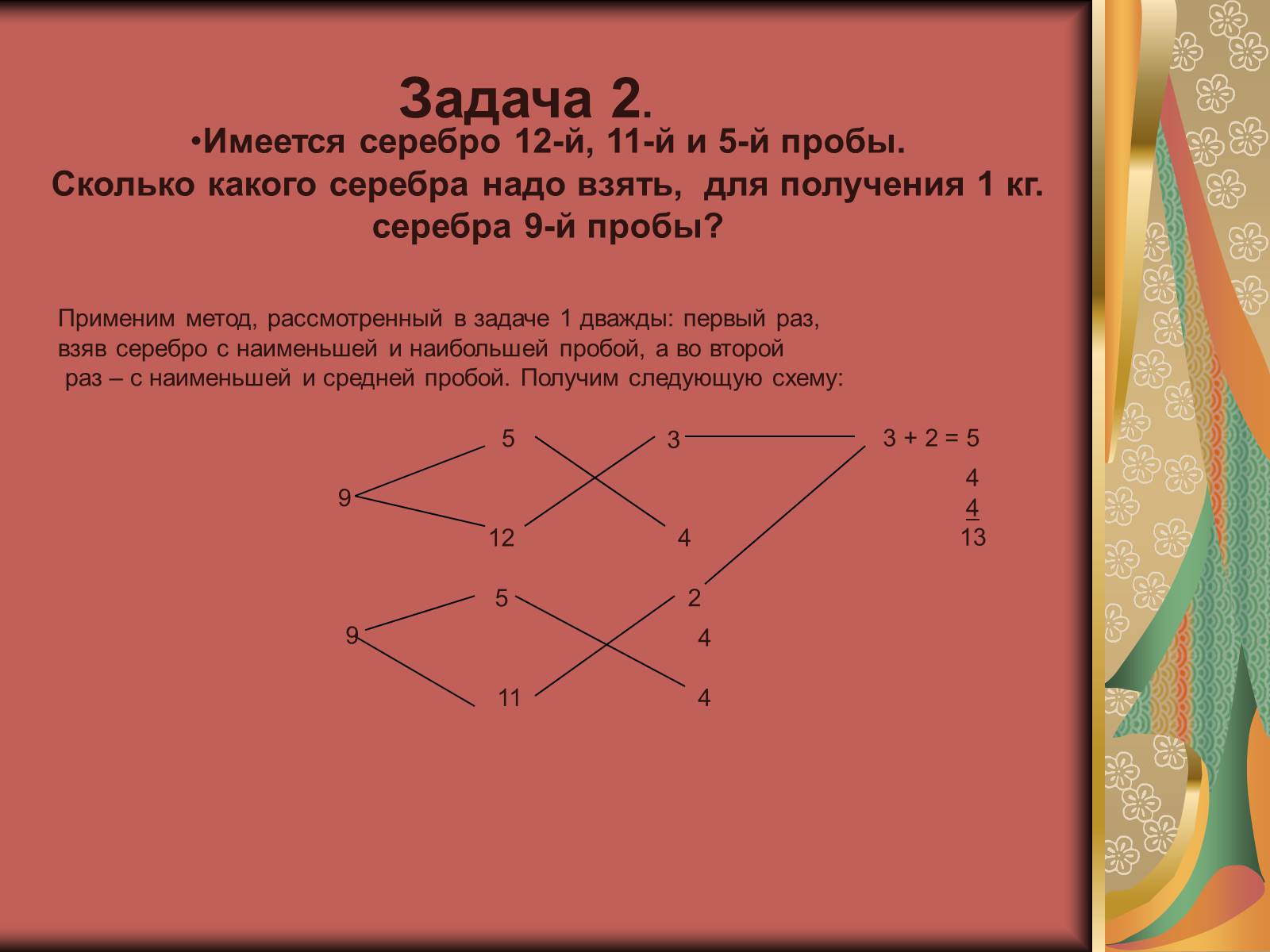
Имеется серебро 12-й, 11-й и 5-й пробы.
Сколько какого серебра надо взять, для получения 1 кг.
серебра 9-й пробы?
Применим метод, рассмотренный в задаче 1 дважды: первый раз,
взяв серебро с наименьшей и наибольшей пробой, а во второй
раз – с наименьшей и средней пробой. Получим следующую схему:
3 + 2 = 5
4
4
13
5
9
5
9
12
4
3
4
2
11
4

При этом найдены доли , в которых нужно сплавлять серебро наибольшей и средней
пробы (4 и 4). Сложив затем доли серебра наименьшей пробы , найденные в первой и
во второй раз (3+2=5), получим долю серебра наименьшей пробы в общем сплаве.
Таким образом, надо взять
кг. серебра 5-й пробы,
кг. серебра 12-й пробы,
Данная задача имеет не единственное решение.
9-й пробы серебро можно получить , сплавляя серебро 5-й и 12-й пробы
в отношении 3:4(1сплав) или серебро 5-й и 11-й пробы в отношении 2:4(2 сплав).
Соединяя 1 и 2 сплавы в любой пропорции, мы будем получать
различные сплавы серебра 9-й пробы.
кг. серебра 11-й пробы.

Задача 3.
Имеется 240г. 70% -ого раствора уксусной кислоты. Нужно получить 6% - ный раствор кислоты. Сколько граммов воды (0%-ный раствор) нужно прибавить к имеющемуся раствору?

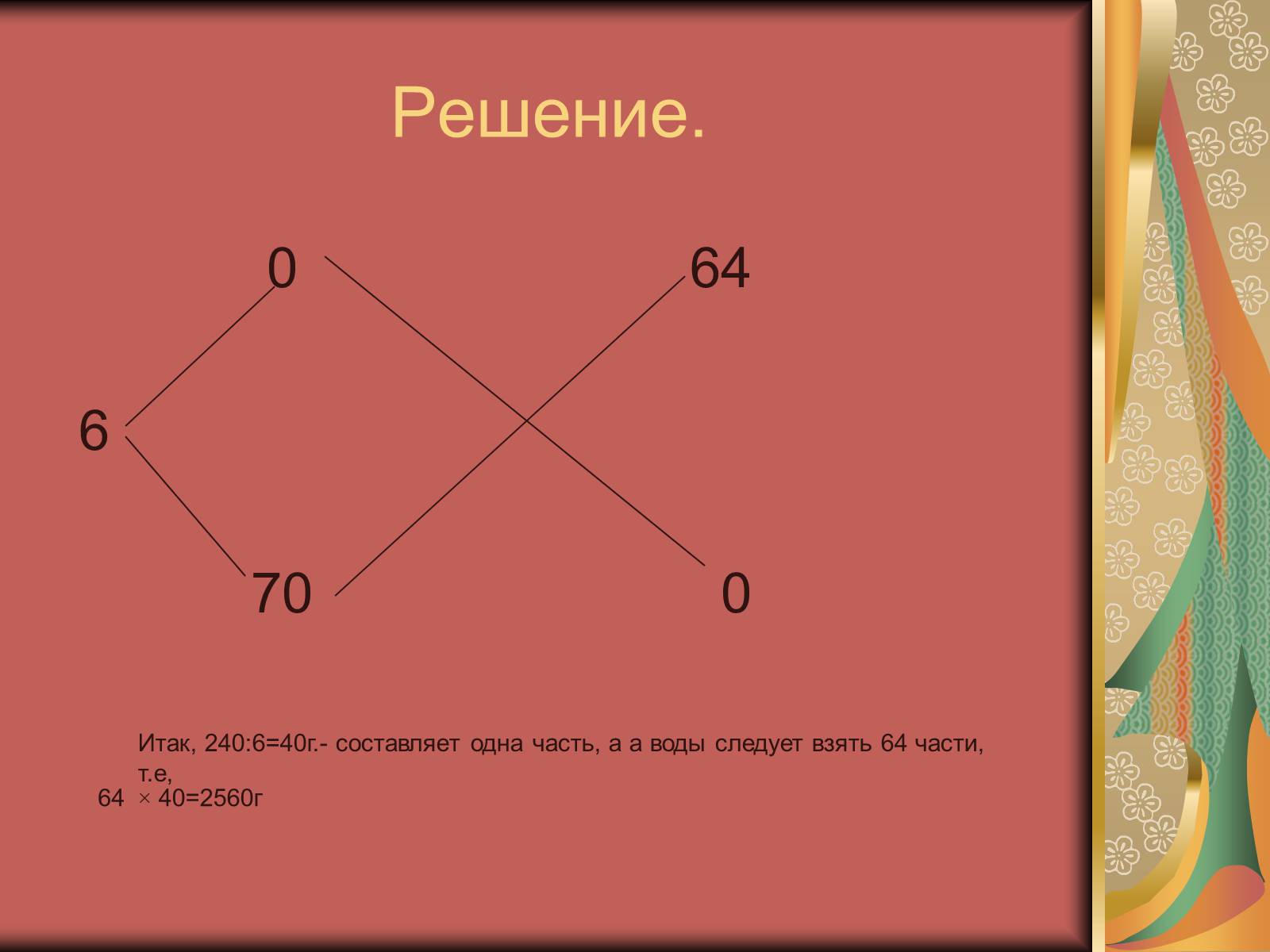
Решение.
0 64
6
70 0
Итак, 240:6=40г.- составляет одна часть, а а воды следует взять 64 части, т.е,
× 40=2560г
64

Применение процентов в жизни.
В настоящее время понимание процентов и умение
производить процентные расчеты, необходимы
каждому человеку:
Прикладное значение этой темы очень велико и
затрагивает финансовую, экономическую,
демографическую и другие сферы нашей жизни.
Изучение процента продиктовано самой жизнью.
Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни.

Заключение.
Я выбрал эту тему потому, что мне нравится математика и я считаю, что математику надо знать хорошо.Я хотел получить полноценные представления о процентах, об их роли в повседневной жизни.
Работа над данной темой , способствовала расширению
моего математического кругозора, развитию умения анализировать, сравнивать, глубоко и прочно усвоив материал. Мне хочется порекомендовать ученикам формулу сложных
процентов и применять её при решении задач на проценты.

Литература
Крамор В.С. «Повторяем и систематизируем школьный курс алгебры и начало анализа». М., «Просвещение» 1990 год.
Журнал «Математика в школе.» 1998г.№5.
Ф.Ф. Нагибин «Математическая шкатулка» М.«Просвещение»1988год.