Презентація на тему «Первісна»

ПервіснаАлгебра і початки аналізу, 11 клас
2013 рік

3. Значення диференціального та інтегрального числення.
4-5. Операції в математиці.
6. Означення первісної.
7. Таблиця первісних.
8-9. Вправи на формування поняття первісної.
10. Основні властивості первісної.
11. Вправа на основну властивість первісної.
12. Графіки первісних для даної функції.
13-15. Вправа на графіки первісних.
16. Правила знаходження первісної.
17. Методичні рекомендації.
Зміст

Сила і загальність методу диференціального й інтегрального числення такі, що не ознайомившись із ними, не можна як слід зрозуміти все значення математики для природознавства, і техніки і навіть повністю оцінити всю красу і принадність самої математичної науки.
А.М. Колмогоров

Операції в математиці
Кожна дія (операція) в математиці має обернену:
додавання-віднімання;
множення-ділення;
піднесення до степеня – добування кореня;
логарифмування – потенціювання;
множення одночлена на многочлен - розкладання многочлена на множники способом винесення спільного множника за дужки.
Деякі з обернених операцій виявилися неоднозначними:
є числа 5 і -5, бо

Основна операція диференціального числення є знаходження похідної даної функції
Обернена операція до диференціювання є: за відомою похідною деякої функції знайти (відновити) саму функцію , яку називають первісною F для відомої функції . Операція знаходження первісної F для даної функції
називається інтегруванням.
Отже, інтегрування є оберненою операцією до операції диференціювання.

Первісна
Означення. Первісною для даної функції y=f(x) на заданому проміжку [a; b] називається така функція F(x), похідна якої для всіх x з інтервалу [a; b] дорівнює f(x), тобто Fʹ(x)=f(x) для всіх x є [a; b].
Наприклад, функція F(x)=x2 є первісною для функції f(x)=2x на проміжку (-∞;∞), оскільки на цій множині виконується рівність (x2)ʹ=2x.
Для функції f(x)=2x первісними будуть функції F(x)=x2+1;F(x)=x2-10; і т.д., тобто загальний вигляд первісних для функції f(x)=2x матимуть вигляд F(x)=x2+С, де С – довільна стала.
Отже, операція інтегрування неоднозначна.

Таблиця первісних
Функція y=f(x)
Загальний вигляд первісної F(x)+C
k, де k - стала
kx+C
xn, де n є Z
sin x
- cos x+C
cos x
sin x+C
tg x + C
- ctg x + C
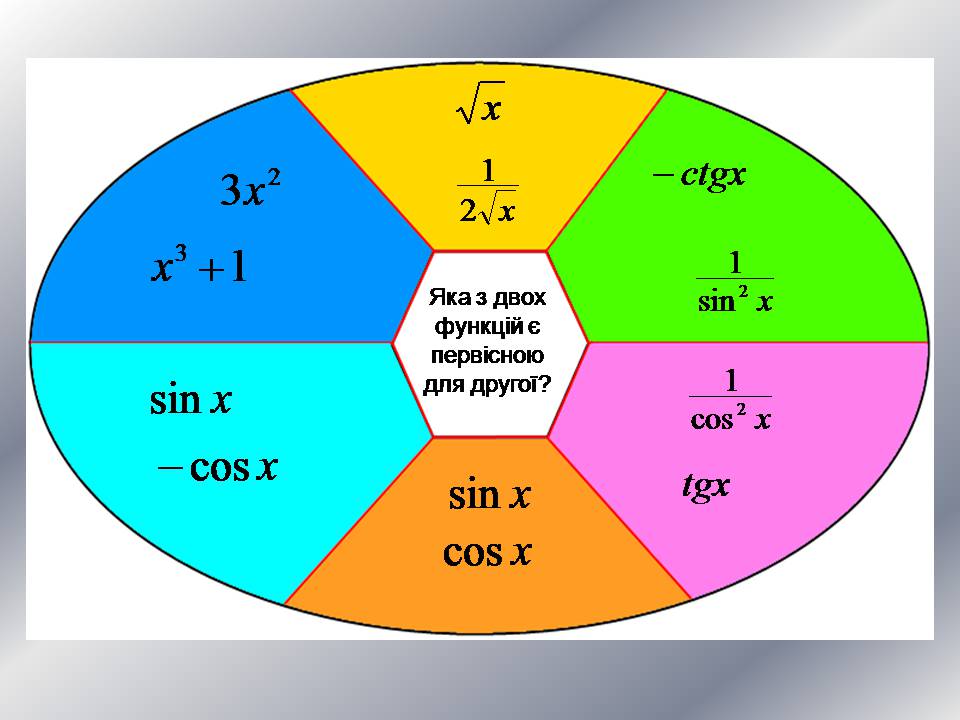
Яка з двох функцій є первісною
для другої?
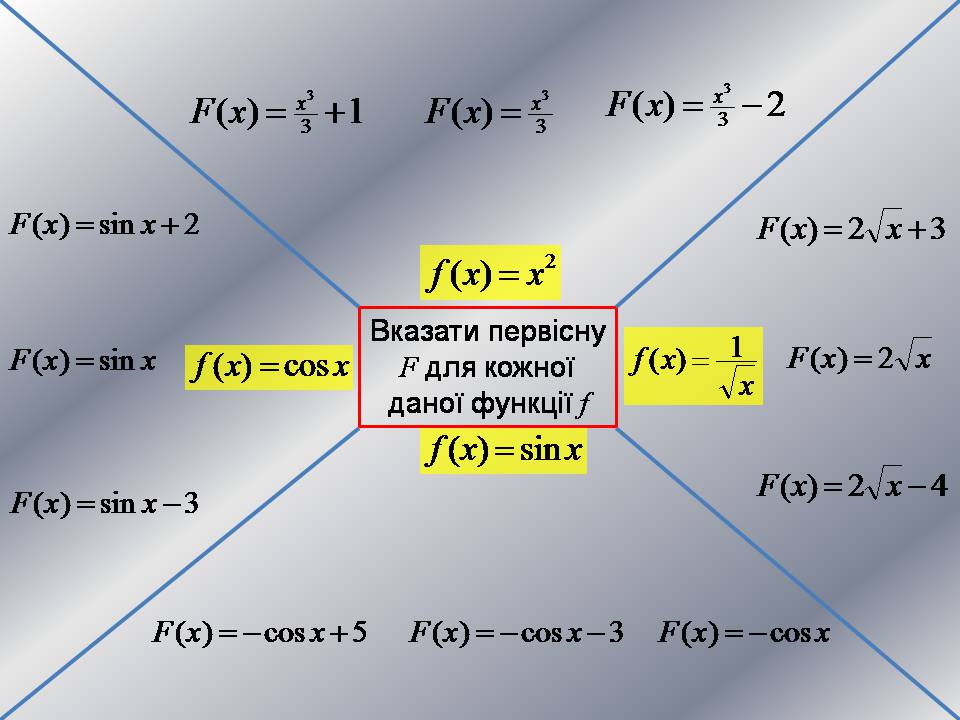
Вказати первісну F для кожної даної функції f
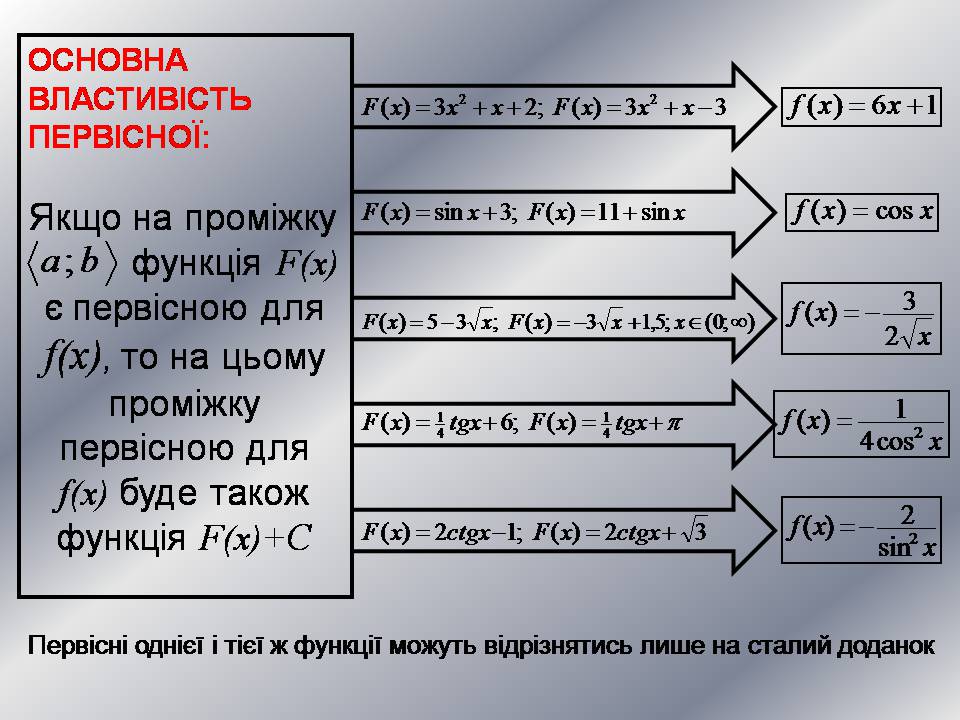
ОСНОВНА ВЛАСТИВІСТЬ
ПЕРВІСНОЇ:
Якщо на проміжку
функція F(x) є первісною для f(x), то на цьому проміжку первісною для f(x) буде також функція F(x)+C
Первісні однієї і тієї ж функції можуть відрізнятись лише на сталий доданок
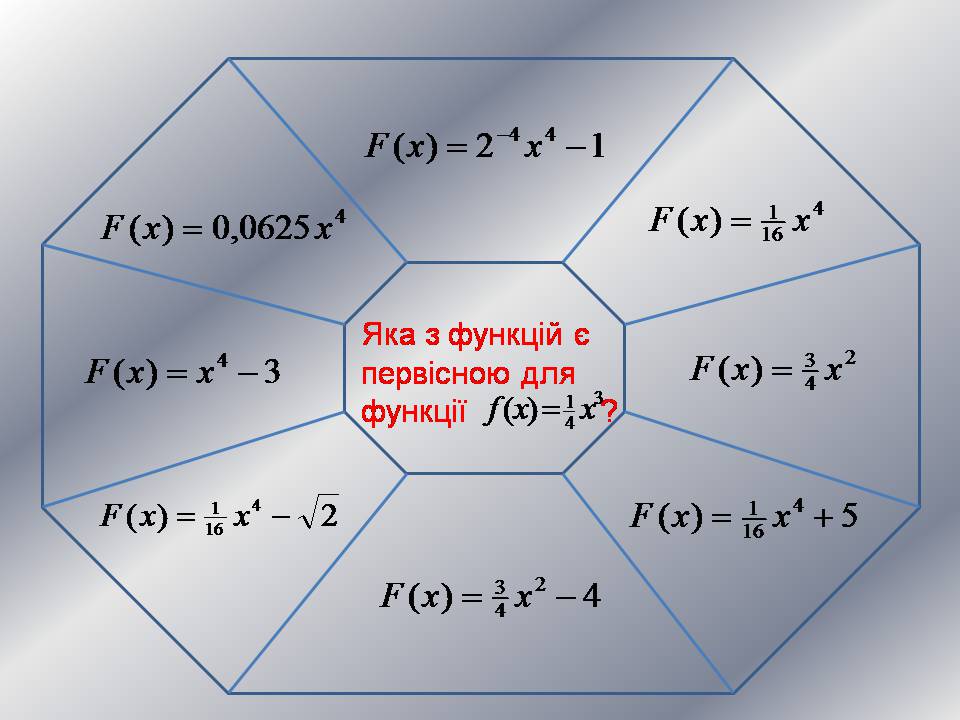
Яка з функцій є первісною для функції ?
x
y
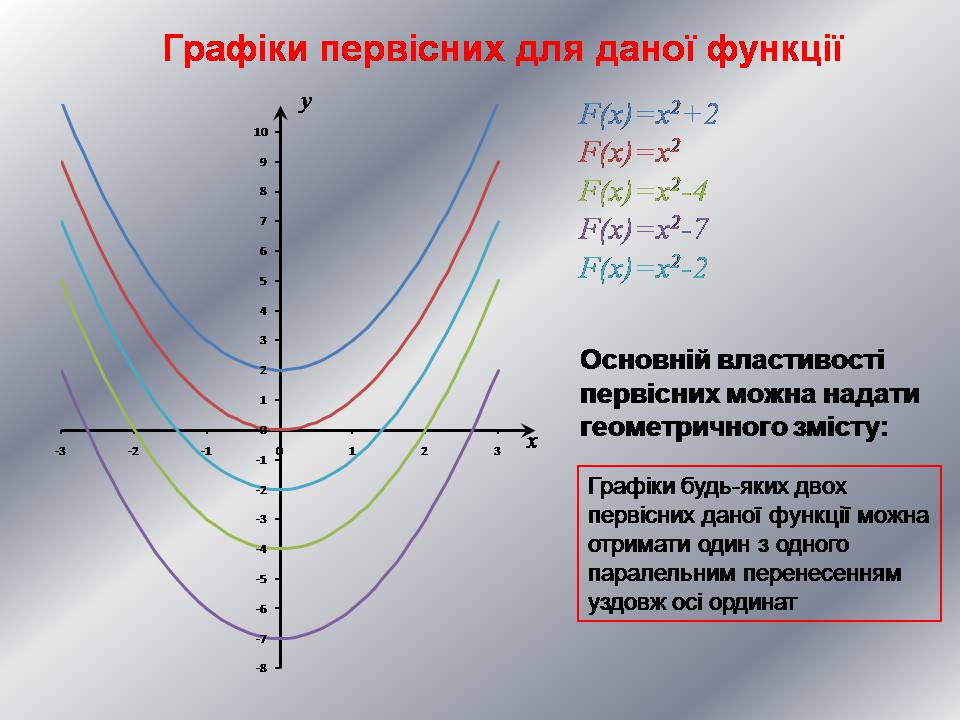
F(x)=x2+2
F(x)=x2
F(x)=x2-4
F(x)=x2-7
F(x)=x2-2
Графіки первісних для даної функції
Основній властивості первісних можна надати геометричного змісту:
Графіки будь-яких двох первісних даної функції можна отримати один з одного паралельним перенесенням уздовж осі ординат
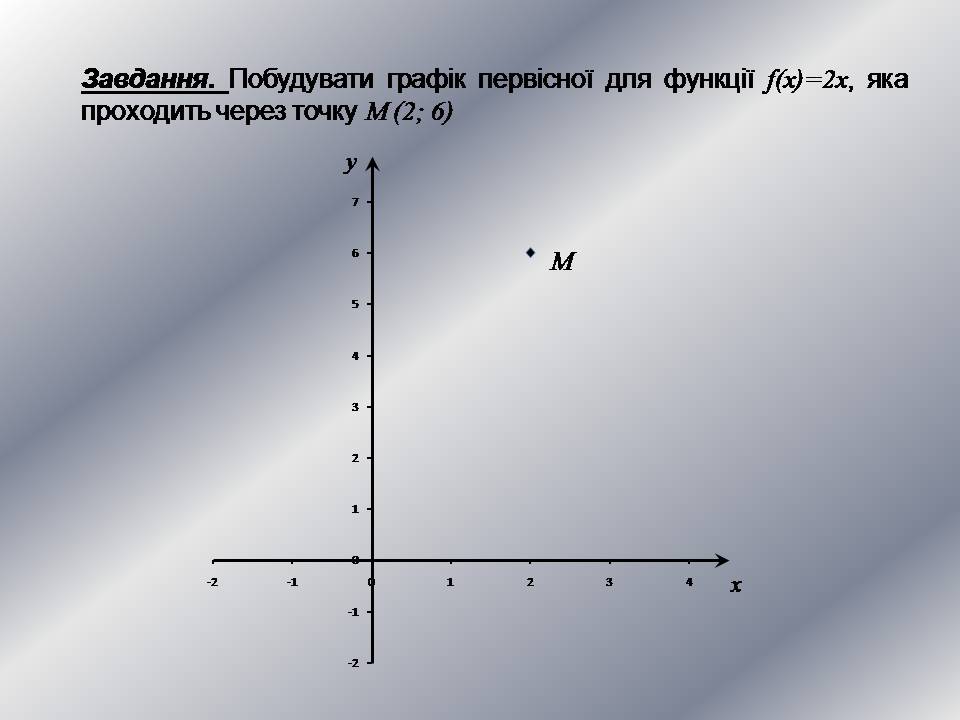
Завдання. Побудувати графік первісної для функції f(x)=2x, яка проходить через точку M (2; 6)
x
y
x
y
x
y
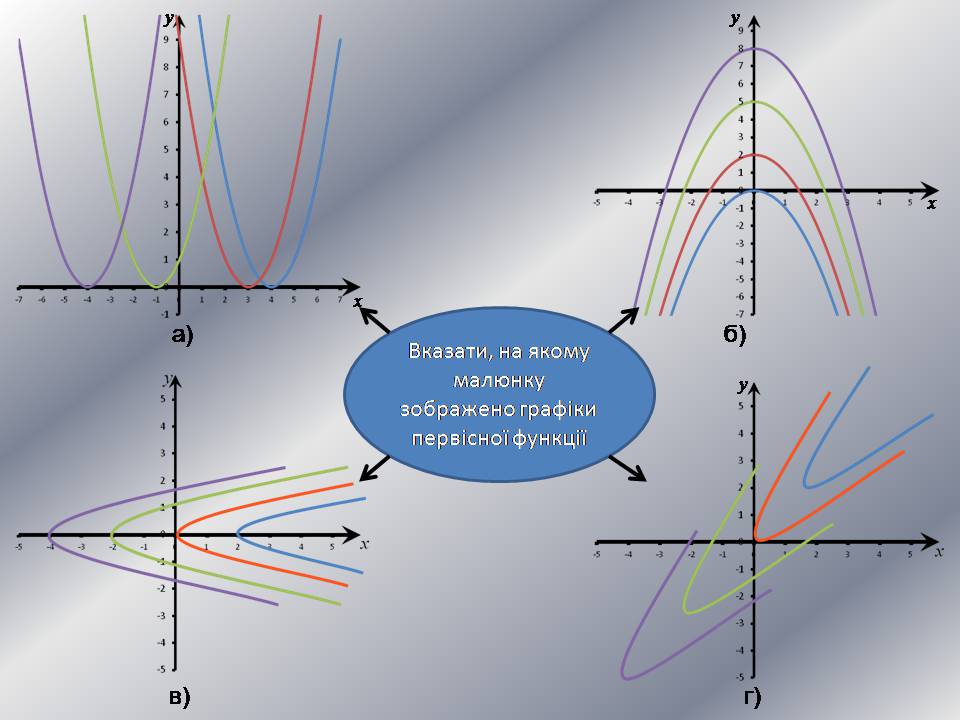
Вказати, на якому малюнку зображено графіки первісної функції
а)
б)
в)
г)
y
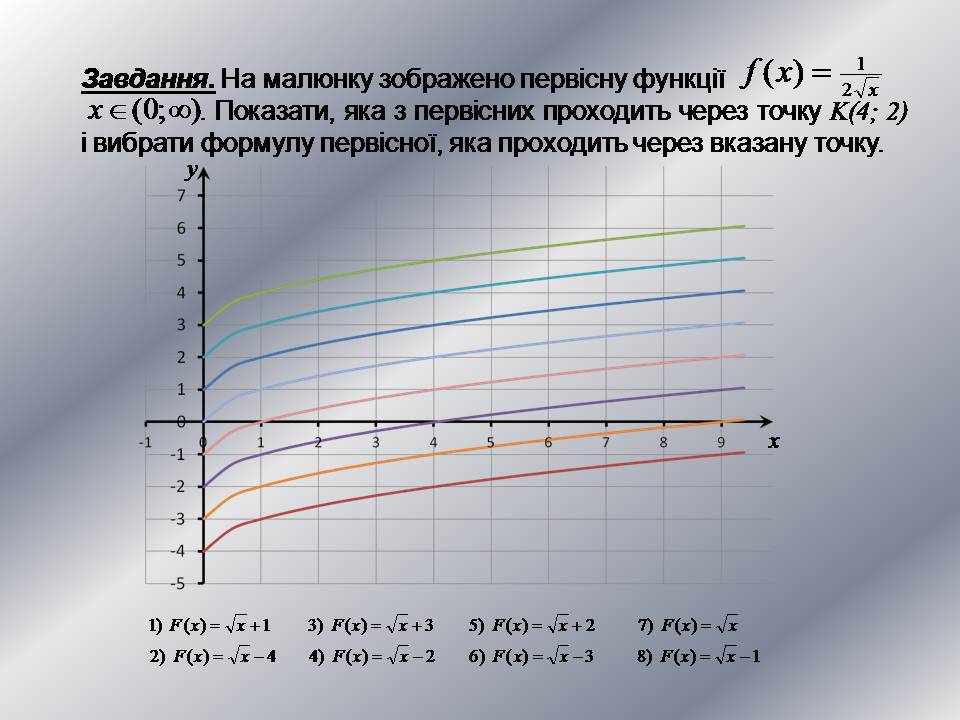
Завдання. На малюнку зображено первісну функції
. Показати, яка з первісних проходить через точку K(4; 2) і вибрати формулу первісної, яка проходить через вказану точку.
x
y

Правила знаходження первісної
Приклад:
І правило знаходження первісної
ІІ правило знаходження первісної
ІІІ правило знаходження первісної
Приклад:
Приклад:

Методичні рекомендації
Слайди 3 -9 використовуються при формуванні поняття первісної
Слайди 10-11 доцільно використати при засвоєнні нового матеріалу про основну властивість первісної
Слайди 12, 14, 15 застосовувати при вивченні графіків первісних для даної функції
Слайд 13 пропонується для самостійної роботи
Слайд 16 бажано використати при вивченні нового матеріалу

Список використаної літератури:
1. Мерзляк А.Г. Алгебра. 11 клас: підруч. для загальноосвіт. навчальн. закладів: академ. рівень, проф. рівень / А. Г. Мерзляк, Д.А. Номіровський, В.Б. Полонський, М. С. Якір. – Х. : Гімназія, 2011. – 431 с.: іл.