Презентація на тему «Об’єми многогранників»

ОБ'ЄМИ
МНОГОГРАННИКІВ

З історії розвитку поняття об'єму геометричних тіл.
У давнину деякі міри маси і об'єму часто збігалися з мірами вартості товару – грошовими одиницями. Зокрема, на Русі основна одиниця маси – гривня – була водночас грошовою одиницею. Гривня – це злиток срібла, маса якого наближено дорівнювала 1 фунту.
У другій половині ХІІІ ст. гривну почали рубати навпіл і називати рублем, який із Х/ став основною грошовою одиницею.
У творах Архімеда та “Началах” Евкліда були виведені формули для знаходження об'ємів многогранників і деяких тіл обертання (циліндра, кулі, конуса та їх частин).
Розробив теорію площ і об'ємів К.М.Е.Жордан (1838 - 1922) – французький математик, один із засновників сучасної математики.
У минулому одиницями вимірювання об'ємів біли міри посудини, що використовувалися для зберігання сипучих і рідких речовин.
Евклід
Приблизно 330 – 277 до н.е.

ПОНЯТТЯ ОБ'ЄМУ
Для простих тіл об'єм – це додатна величина, числове значення якої має такі властивості:
1. Рівні тіла мають рівні об'єми.
2. Якщо тіло розбито на частини, які є простими тілами, то об'єм цього тіла дорівнює сумі об'ємів його частин.
3. Об'єм куба, ребро якого дорівнює одиниці довжини, дорівнює одиниці.

a
b
c
A
B
С
D
A1
B1
D1
С1
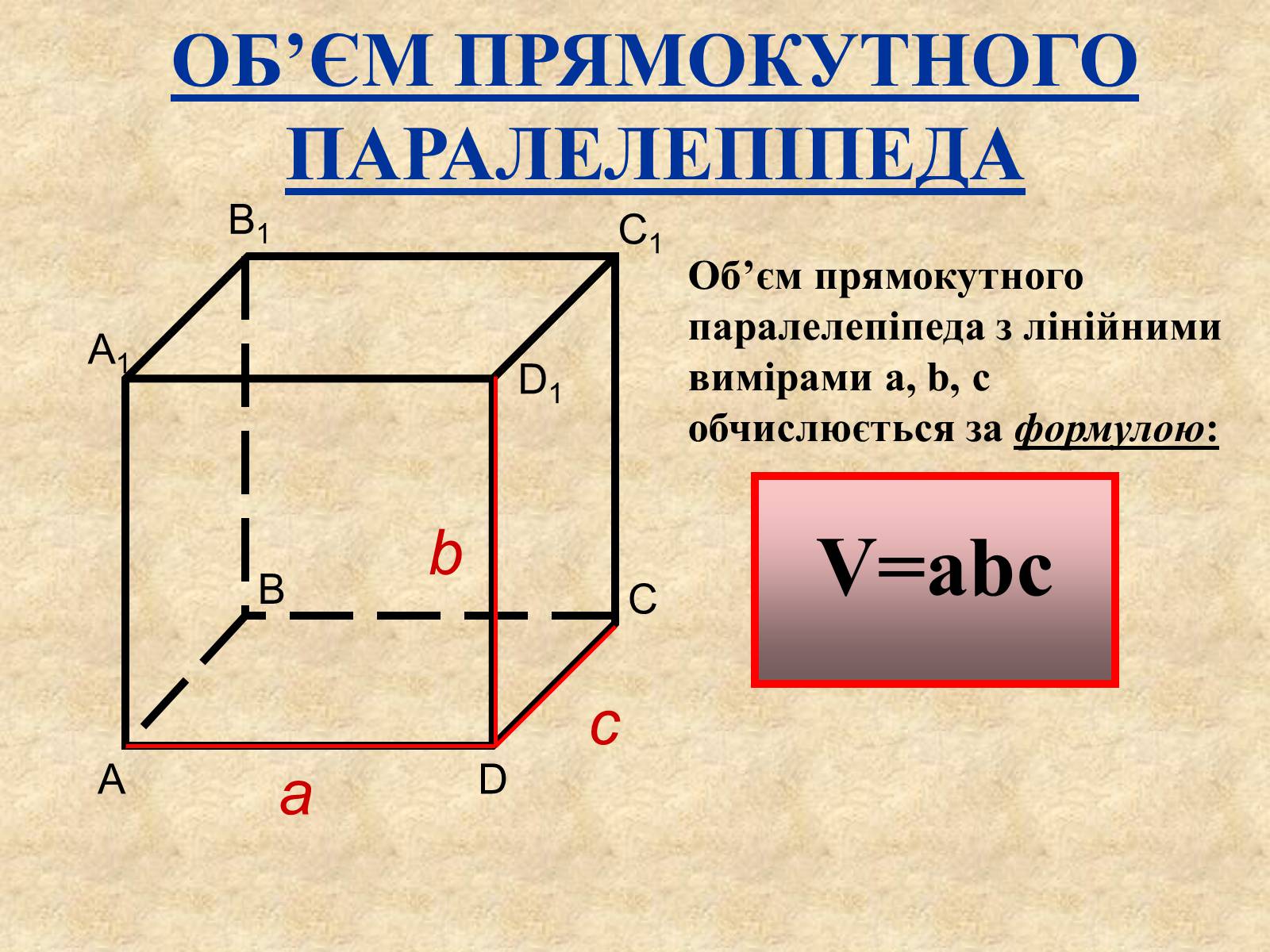
ОБ'ЄМ ПРЯМОКУТНОГО ПАРАЛЕЛЕПІПЕДА
Об'єм прямокутного паралелепіпеда з лінійними вимірами a, b, c обчислюється за формулою:
V=abc

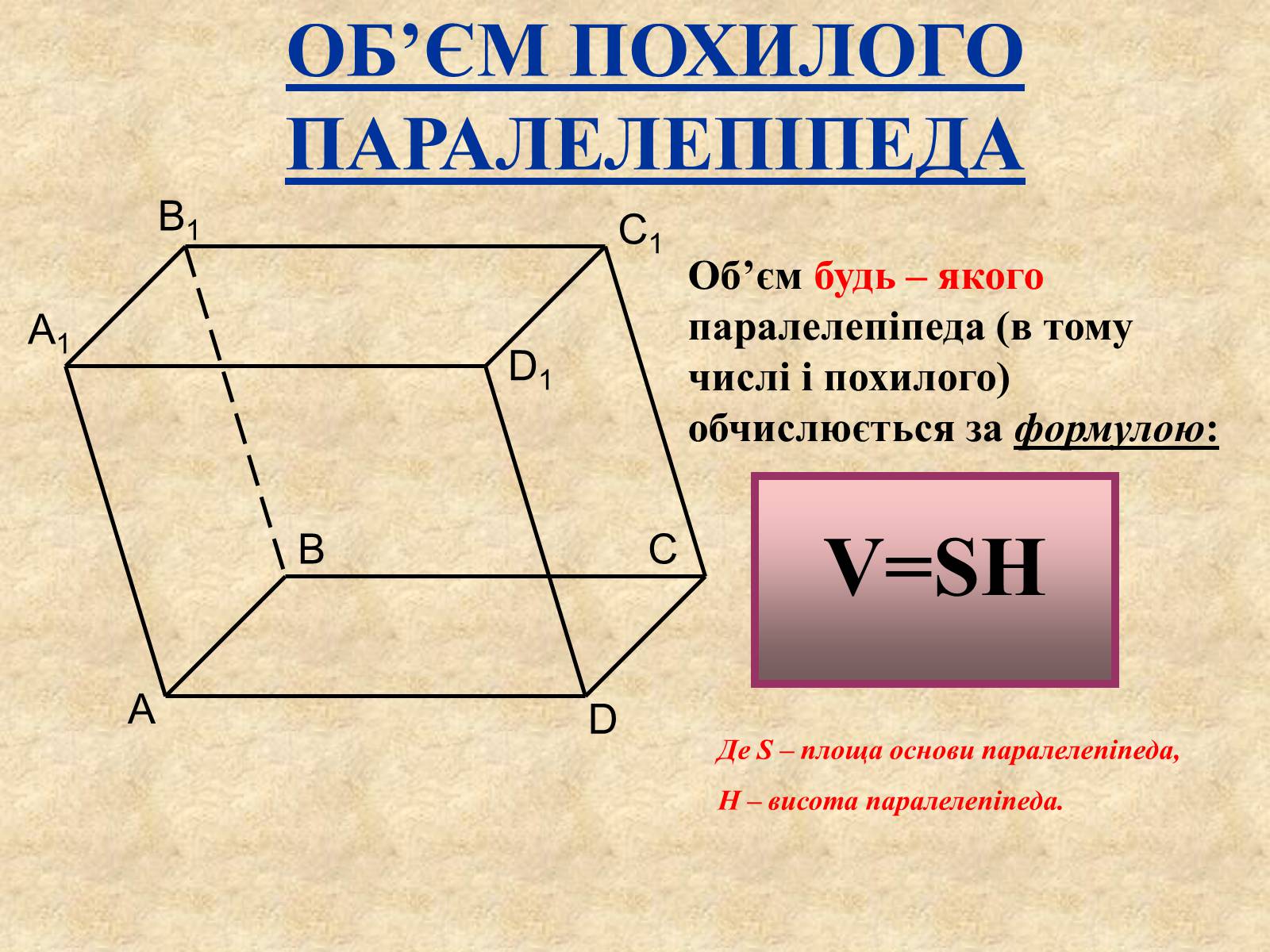
ОБ'ЄМ ПОХИЛОГО ПАРАЛЕЛЕПІПЕДА
Об'єм будь – якого паралелепіпеда (в тому числі і похилого) обчислюється за формулою:
V=SH
A
B
С
D
A1
B1
D1
С1
Де S – площа основи паралелепіпеда,
H – висота паралелепіпеда.

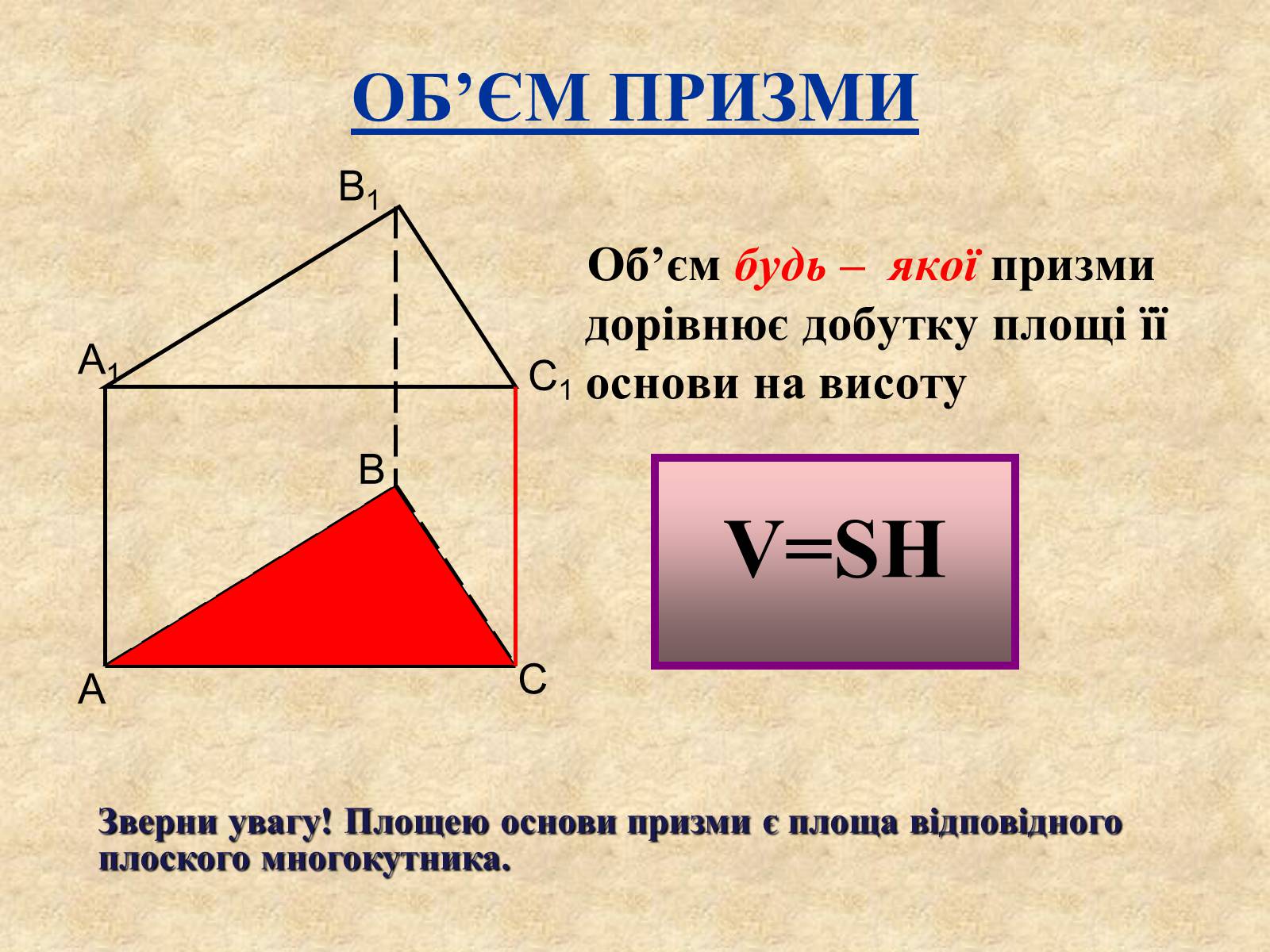
ОБ'ЄМ ПРИЗМИ
Об'єм будь – якої призми дорівнює добутку площі її основи на висоту
V=SH
A
B
С
A1
B1
С1
Зверни увагу! Площею основи призми є площа відповідного плоского многокутника.

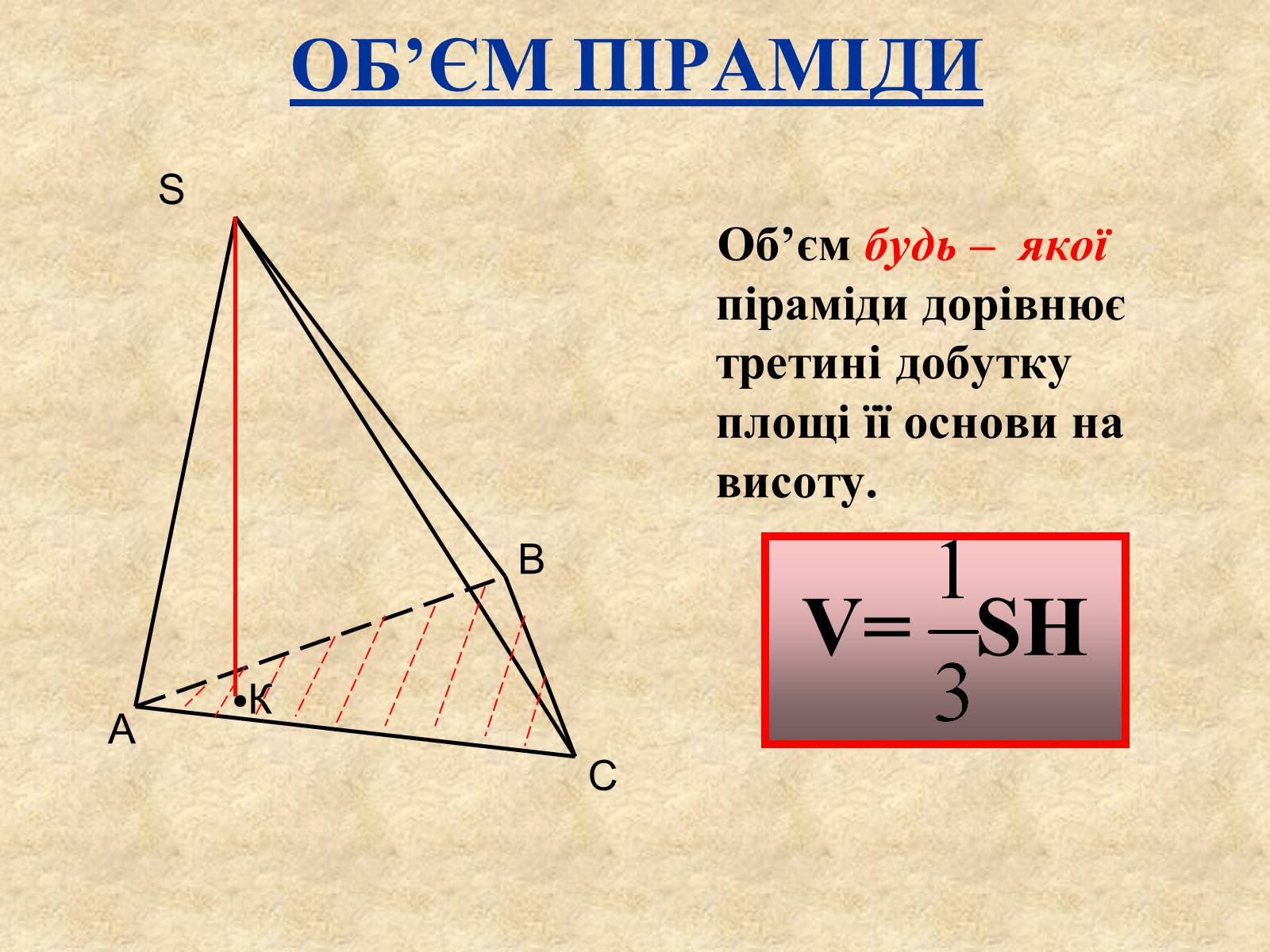
ОБ'ЄМ ПІРАМІДИ
Об'єм будь – якої піраміди дорівнює третині добутку площі її основи на висоту.
A
B
S
С
V= SH
К

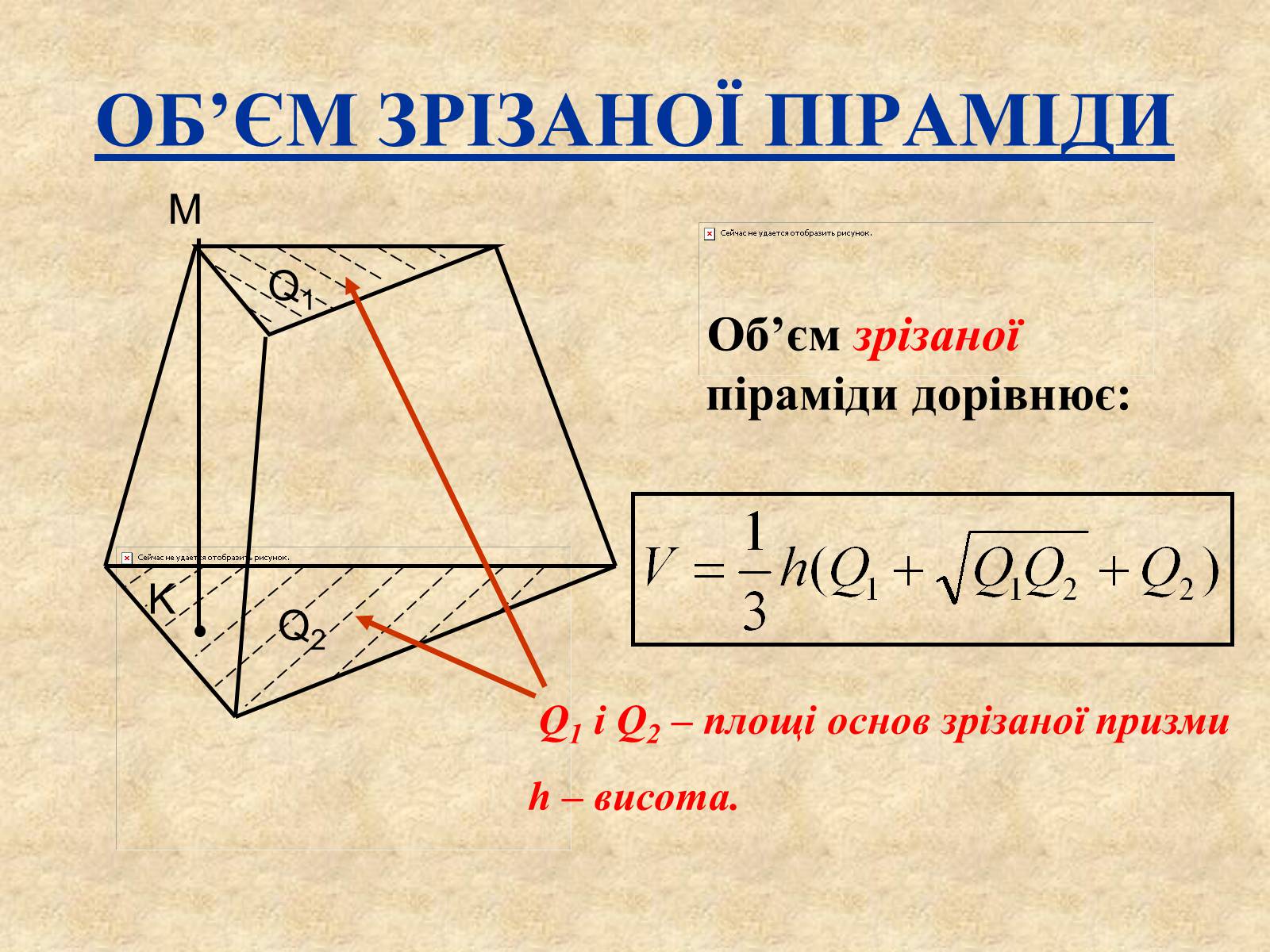
ОБ'ЄМ ЗРІЗАНОЇ ПІРАМІДИ
Q1
Q2
Об'єм зрізаної піраміди дорівнює:
M
K
Q1 і Q2 – площі основ зрізаної призми
h – висота.