Презентація на тему «Арифметична прогресія та її властивості»

Арифметична прогресія та її властивості

Означення
а1; а2; а3; а4
а2 = а1 + d
a3 = a2 + d
d – різниця арифметичної прогресії
an+1 = an + d -рекурентна формула
Арифметичною прогресією називають послідовність, кожний член якої, починаючи із другого, дорівнює попередньому члену, до якого додається одне й те ж число.
скінченна
нескінченна
Арифметична прогресія

Властивість 1
an =
Будь-який член арифметичної прогресії, починаючи з другого, є середнім арифметичним двох сусідніх з ним членів.
an-1 + an+1
2

Властивість 2
Сума будь-яких двох членів скінченної арифметичної прогресії, які рівновіддалені від її крайніх членів, дорівнює сумі крайніх членів цієї прогресії.
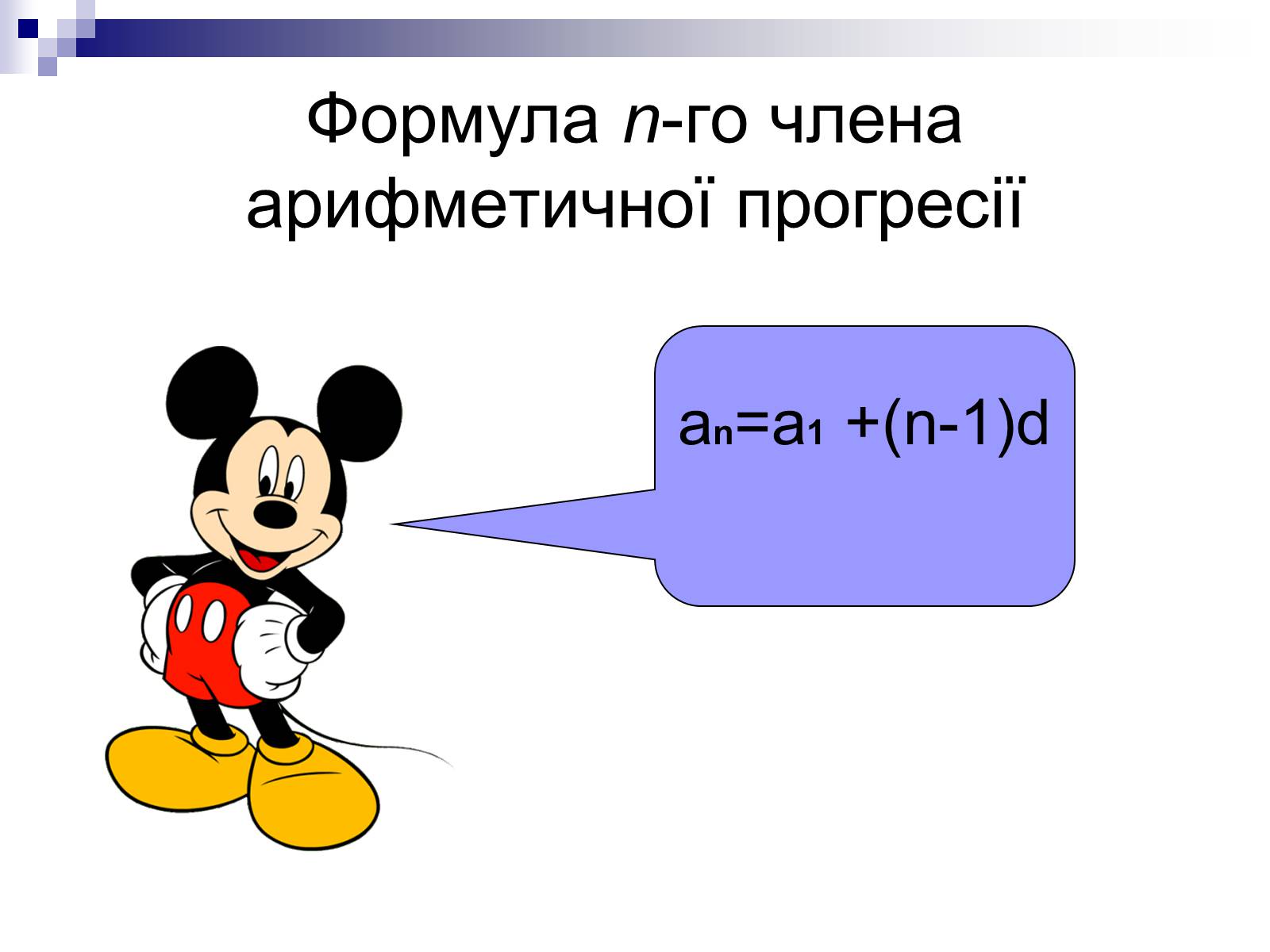
Формула n-го члена арифметичної прогресії
an=a1 +(n-1)d

Формула суми перших n членів арифметичної прогресії
Sn=
2a1+(n-1)d
* n
2

Задача 1
Знайти другий і третій член арифметичної прогресії, якщо а1=2; d=1,5.

Розв'язання
а2=a1+d;
a2=2+1,5;
a2=3,5.
Відповідь: а2=3,5; а3=5
a3=a2+d;
a3=3,5+1,5;
a3=5.

Задача 2
Знайти різницю та третій член арифметичної прогресії, у якій а1=4, а2=7.

Розв'язання
d=a2-a1;
d=7-4;
d=3.
a3=a2+d;
a3=7+3;
a3=10
Відповідь: d=3; a3=10.

Задача 3
Чи є послідовність чисел 5; 10: 15; 20 арифметичною прогресією?

Розв'язання
Позначимо члени заданої послідовності:
а1=5; а2=10; а3=15; а4=20.
Знайдемо різниці наступного та попереднього членів послідовності:
а2-а1=10-5=5;
а3-а2=15-5=5;
а4-а3=20-15=5.
Оскільки одержані різниці дорівнюють одному й тому ж числу 5, то ця послідовність є арифметичною прогресією.