Презентація на тему «Обобщение и уточнение Ньютоном законов Кеплера»
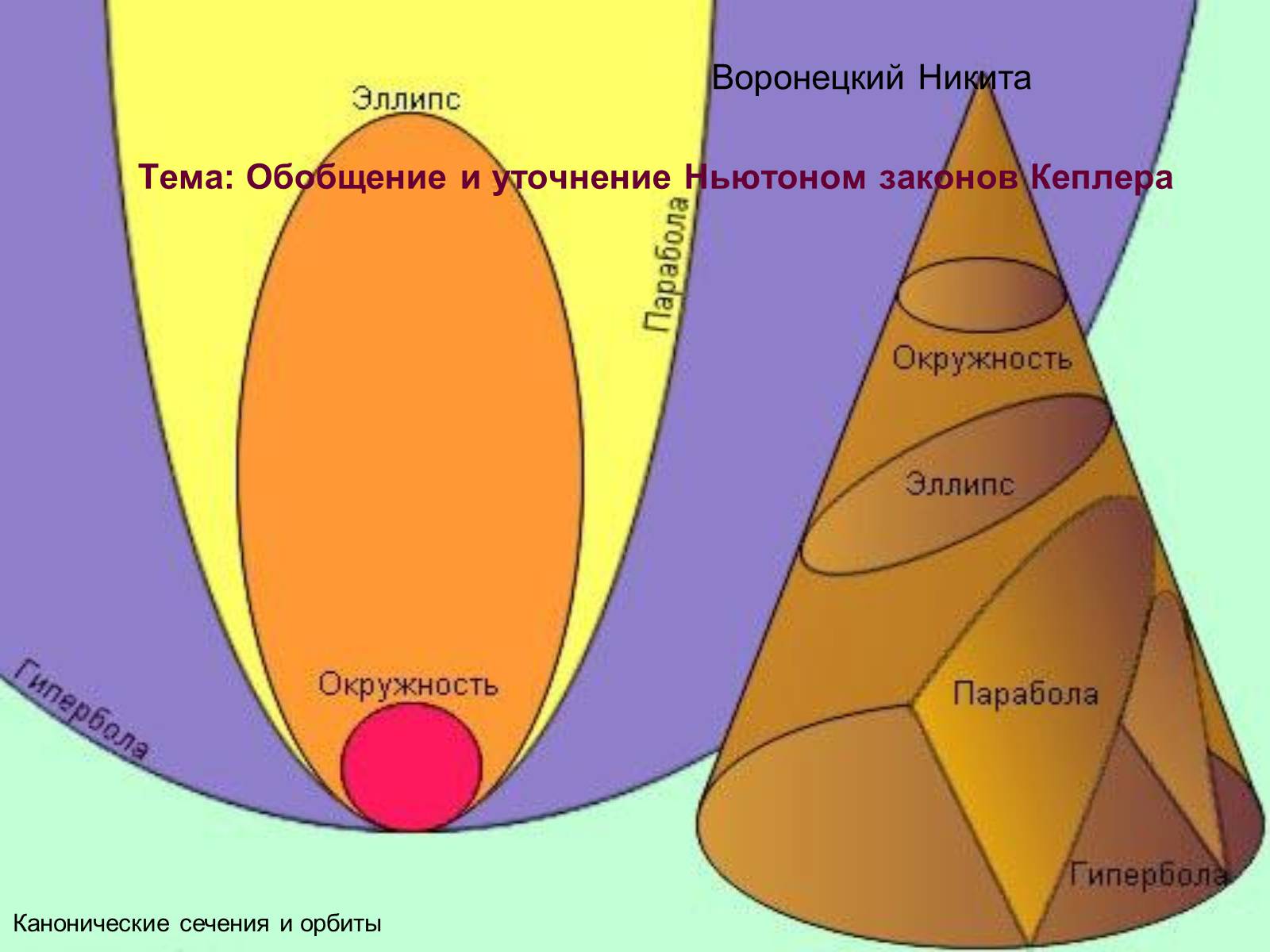
Тема: Обобщение и уточнение Ньютоном законов Кеплера
Канонические сечения и орбиты
Воронецкий Никита

Иоганн Кеплер открыл свои законы эмпирическим путём
I. Все планеты Солнечной системы вращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце.II. Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади: скорость движения планет максимальна в перигелии и минимальна в афелии.III. Квадраты периодов обращения планет вокруг Солнца соотносятся
между собой, как кубы их средних расстояний от Солнца:
И. Ньютон в 1686г излагает учение о всемирном тяготении и теорию движения небесных тел.
Сила тяготения между Солнцем и планетой пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
Гравитация – общее свойство всех тел природы.
Для небесных тел объясняет:
почти все движения
многие процессы образование и развитие небесных тел
Исаак НЬЮТОН (1643-1727)

Законы Кеплера ►как движутся,
ЗВт ► почему так движутся
Понятие “небесная механика” ввел в 1799г Пьер Симон Лапласс (1749-1827, Франция), который в астрономии исследовал сложные случаи возмущенного движения космических тел (вековые возмущения Юпитера, Сатурна, Луны; фигуры планет; движение полюсов Земли; первая теория движения спутников Юпитера и динамической теории приливов; обоснование механической устойчивости Солнечной системы). Пятитомный "Трактат о небесной механике" стал классическим трудом и в течении 50 лет был основным руководством для астрономов в данном разделе науки.
4 закона (3 закона Кеплера и 3Вт) основные законы
Небесной механики – раздела астрономии, исследующего движение небесных тел под действием взаимного притяжения.

Джон Адамс (1819-1892, Англия) – студент, начав с 1844г расчеты, к сентябрю 1845г указал, где искать новую планету. Но ни профессор Кембриджского университета Уэллис, ни директор Гринвичской обсерватории Джорж Эри (1801-1892) не предприняли ее поиска –проигнорировали расчеты молодого математика.
Возмущения, открытие планет
С древности людям известны 5 планет, видимые невооруженным глазом.
13 марта 1781г Вильям Гершель открыл Уран (считал, что это комета) и лишь через 4 месяца российский астроном А.И. Лексель (1740 –1784) указал, что это планета.
Астрономы рассчитали орбиту Урана и выявили его отклонение от Кеплеровской орбиты. Почему?
Изменения характеристик движения космических тел вследствие притяжения со стороны других космических тел, помимо центрального, называются возмущениями и наблюдаются в виде отклонений от траекторий, вычисленных на основе законов Кеплера.
1. Действие Сатурна или Юпитера (выяснилось, – нет).2. За Ураном есть еще планета?
В. Гершель (1738 – 1822)
Урбен Леверье (Франция) так же решил сверхсложную задачу в 1846г используя теорию возмущений, опубликовал три статьи и 18 сентября отправил письмо астроному Берлинской обсерватории Иоганну Галле, который 23 сентября 1846г в 52' от указанного места открыл 8- ю планету – Нептун.
Вид Урана с Земли в телескоп
Вид Нептуна в наземный телескоп
Урбен Леверье (1811-1877)
Иоганн Галле (1812-1910)

Первый закон Кеплера
Допуская неподвижность одного тела, Ньютон доказывает: Под действием силы тяготения одно небесное тело по отношению к другому может двигаться по окружности, эллипсу, параболе и гиперболе (виды канонического сечения)
Первому закону подчиняется и форма орбиты искусственных небесных тел, которая зависит от модуля и направления начальной скорости.
Орбита каждой планеты есть эллипс, в одном из фокусов которого находится Солнце.
Форма эллипса характеризуется эксцентриситетом.
Законы Кеплера в формулировке Ньютона
Сформулировав задачу двух тел (m1, m2 со скоростями v1, v2) и решая ее с помощью высшей математики (находя коэффициенты тел под действием силы взаимного притяжения) Ньютон вывел все законы Кеплера из Закона Всемирного тяготения и при этом открыл и разработал дифференциальное и интегральное исчисление.
Спутниками космических объектов называются объекты, вращающиеся вокруг них (общего центра тяжести) под действием сил тяготения.
1-я круговая – υo=7,91км/с; эллиптическая: 2 - υ=9км/с, 3 - υ=11,1км/с; 2-я параболическая 4 - υ2= υo.√2 =11,19 км/с

Зависимость орбиты ИСЗ от начальной скорости
Вторая космическая скорость υ2= υ1.√2 =11,19 км/с. Тело движется по параболе и навсегда уходит от Земли, становясь ИС Солнца. Впервые «Луна -1», 2.01.1959г.
Первая космическая (круговая) скорость. Для Земли υ1=7, 91 км/с. Тело становится ИСЗ. Впервые «Спутник-1», 4.10.1957г.
Эллиптическая (разной степени вытянутости орбита): от υ1=7, 91 км/с до υ2= 11,19 км/с. При υ = 11,1 км/с облет Луны - сильно вытянутый эллипс. 07.10.1959г КА впервые облетел Луну, впервые применив гравитационный маневр и впервые сфотографировал обратную сторону Луны («Луна-3»/СССР/)
Для полета к ближайшим планетам требуется скорость υ3= υ2.√2 =16,67 км/с (впервые «Венера-1», 12.02.1961г). Для того, чтобы КА запущенный с Земли покинул пределы Солнечной системы, необходимо создать третью космическую скоростью (сумма скорости движения Земли вокруг Солнца и II космической скорости КА относительно Земли. υIII = 42 км/с.
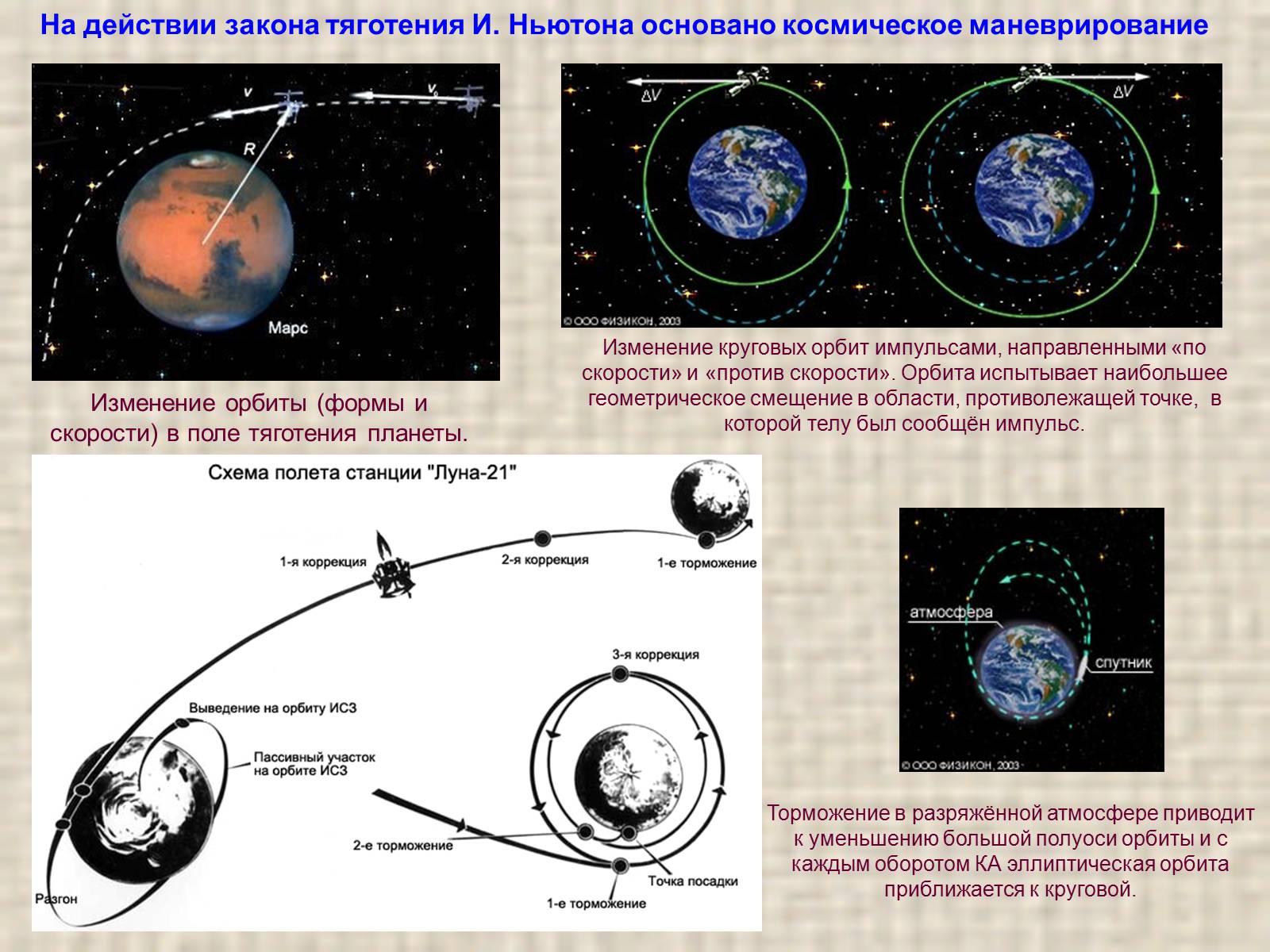
Изменение орбиты (формы и скорости) в поле тяготения планеты.
На действии закона тяготения И. Ньютона основано космическое маневрирование
Изменение круговых орбит импульсами, направленными «по скорости» и «против скорости». Орбита испытывает наибольшее геометрическое смещение в области, противолежащей точке, в которой телу был сообщён импульс.
Торможение в разряжённой атмосфере приводит к уменьшению большой полуоси орбиты и с каждым оборотом КА эллиптическая орбита приближается к круговой.

Второй закон КеплераРадиус-вектор планеты за равные промежутки времени описывает равные площади. При движении планеты по орбите: при приближении к Солнцу - скорость возрастает, кинетическая энергия возрастает, потенциальная убывает, а при удалении планеты – наоборот. Закон не потребовал уточнения.
Третий закон КеплераКвадраты сидерических периодов обращения двух планет относятся как кубы больших полуосей их орбит.
И. Ньютон решая задачу двух тел, вращающихся вокруг общего центра, найдя их получаемые ускорения из закона всемирного тяготения и через угловую скорость центростремительное ускорение, получил уточненный 3-й закон Кеплера с массами тел.
Законы Кеплера в формулировке Ньютона
Или для обращающихся вокруг Солнца