Презентація на тему «Закони Кеплера» (варіант 6)

ЗАКОНИ КЕПЛЕРА

Йога́ннес Ке́плер
німецький філософ, математик, астроном, астролог і оптик, відомий насамперед відкриттям законів руху планет, названих законами Кеплера на його честь. В обчислювальній математиці на його честь названо метод наближеного обчислення інтегралів. 

ПЕРШИЙ ЗАКОН КЕПЛЕРА
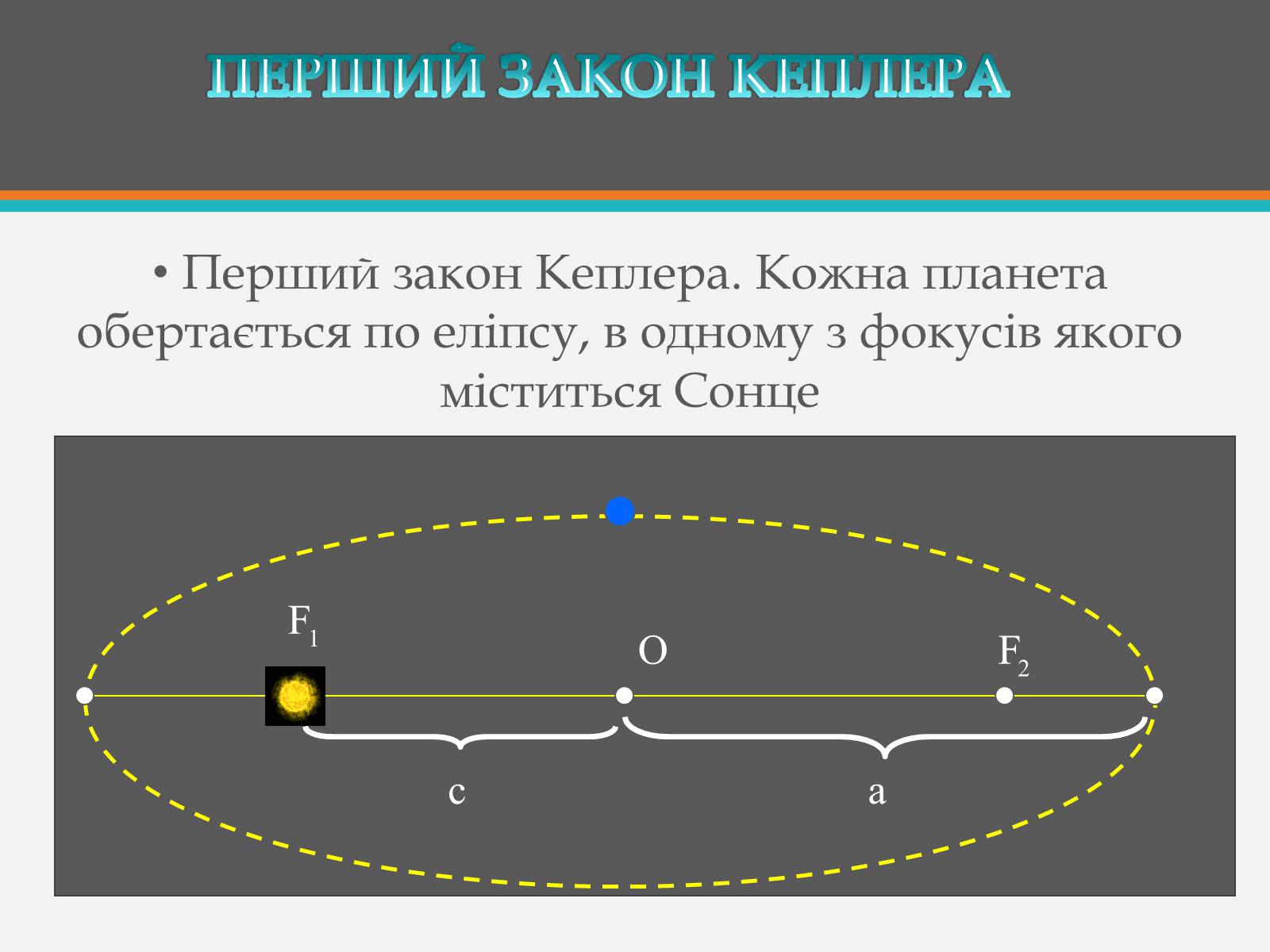
Перший закон Кеплера. Кожна планета обертається по еліпсу, в одному з фокусів якого міститься Сонце
О
F
1
F
2
а
с

Еліпсом називається плоска замкнута крива, властивість якої полягає в тому, що сума відстаней від кожної її точки до двох точок, які називаються фокусами, залишається сталою. Ця сума відстаней дорівнює довжині великої осі DА еліпса.

F
F
О
1
2
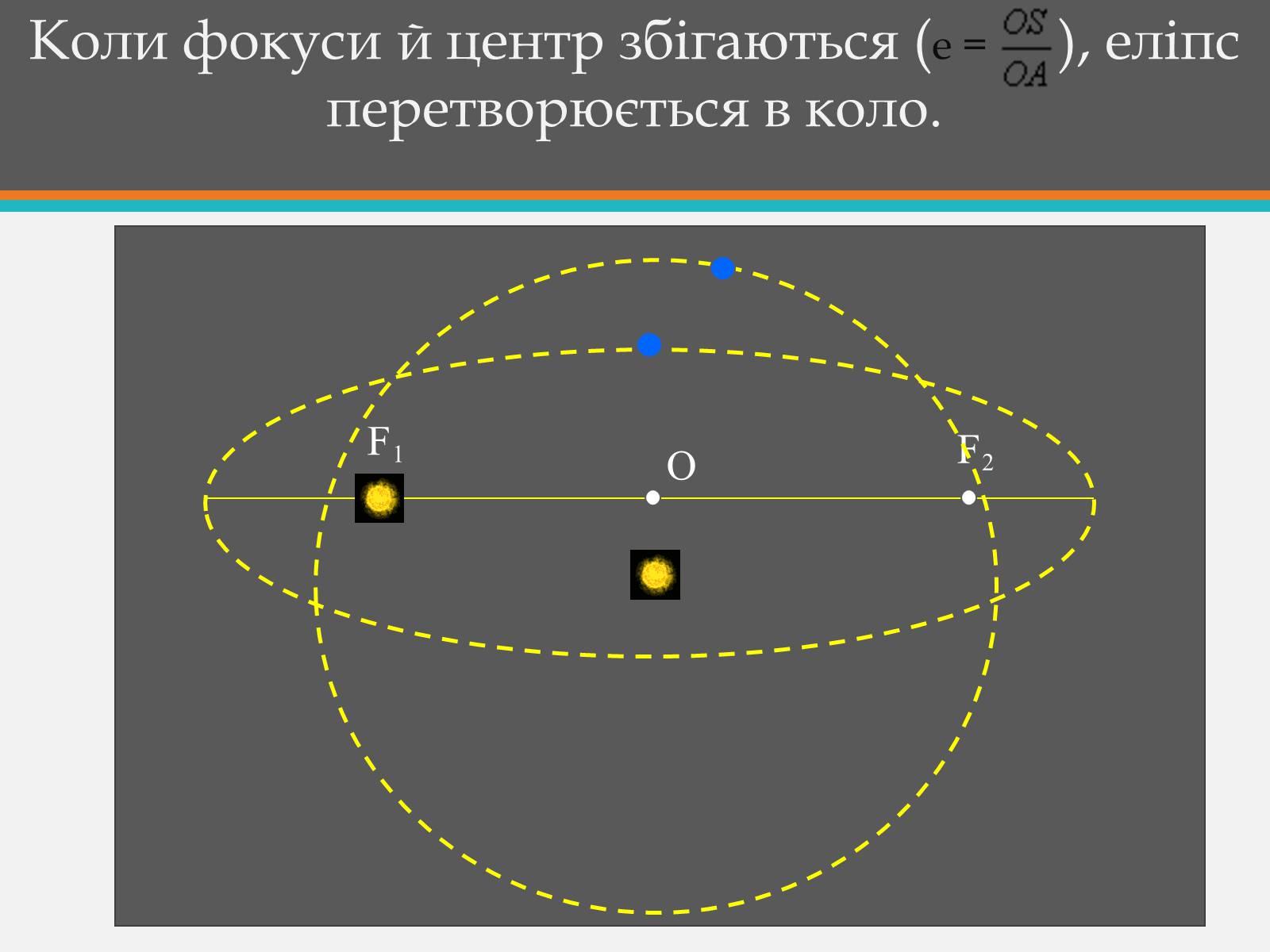
Коли фокуси й центр збігаються (е =  ), еліпс перетворюється в коло.

ДРУГИЙ ЗАКОН КЕПЛЕРА
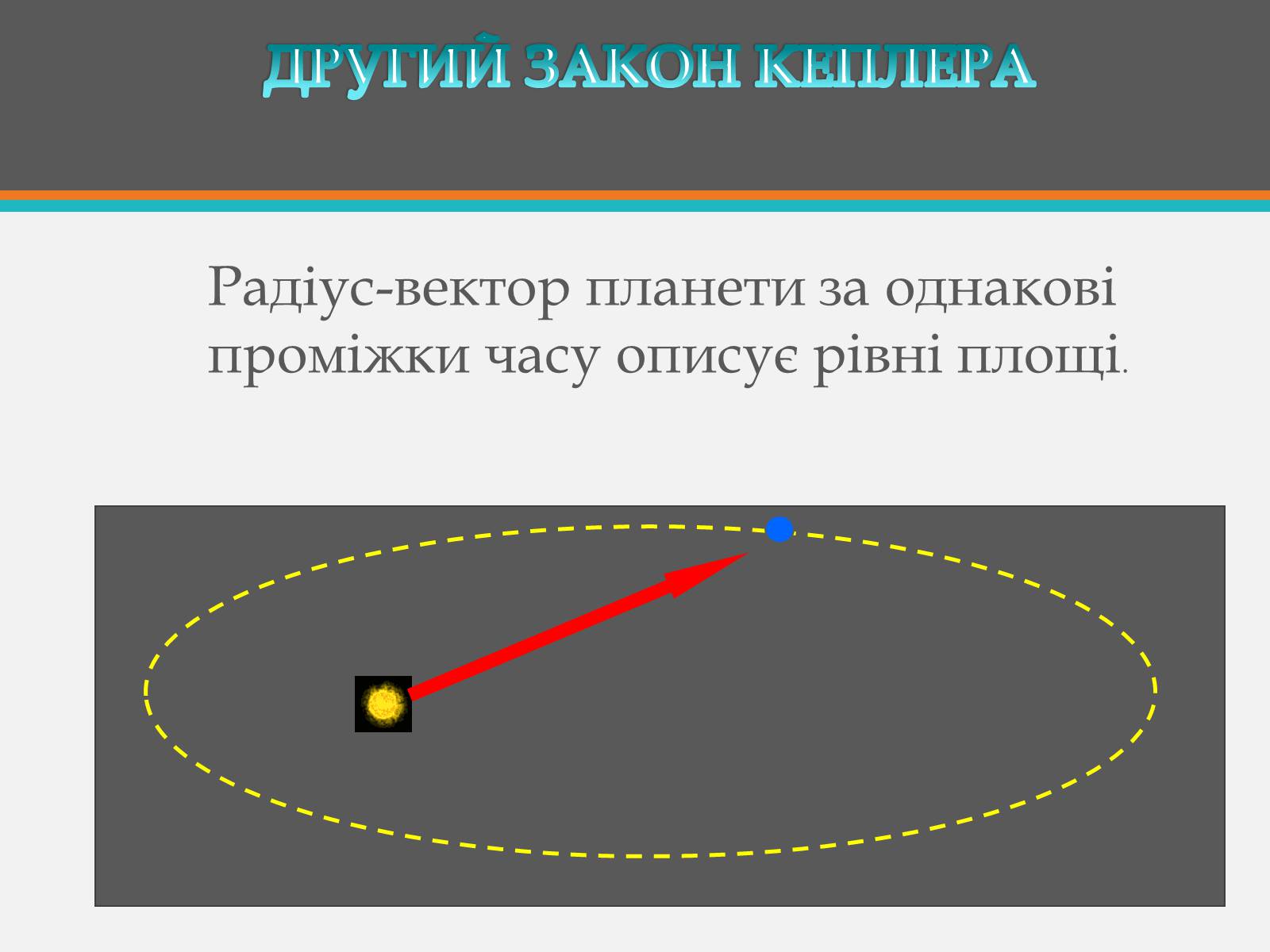
Радіус-вектор планети за однакові проміжки часу описує рівні площі.

П
Перигелий
А
Афелий
S
H
D
C
K
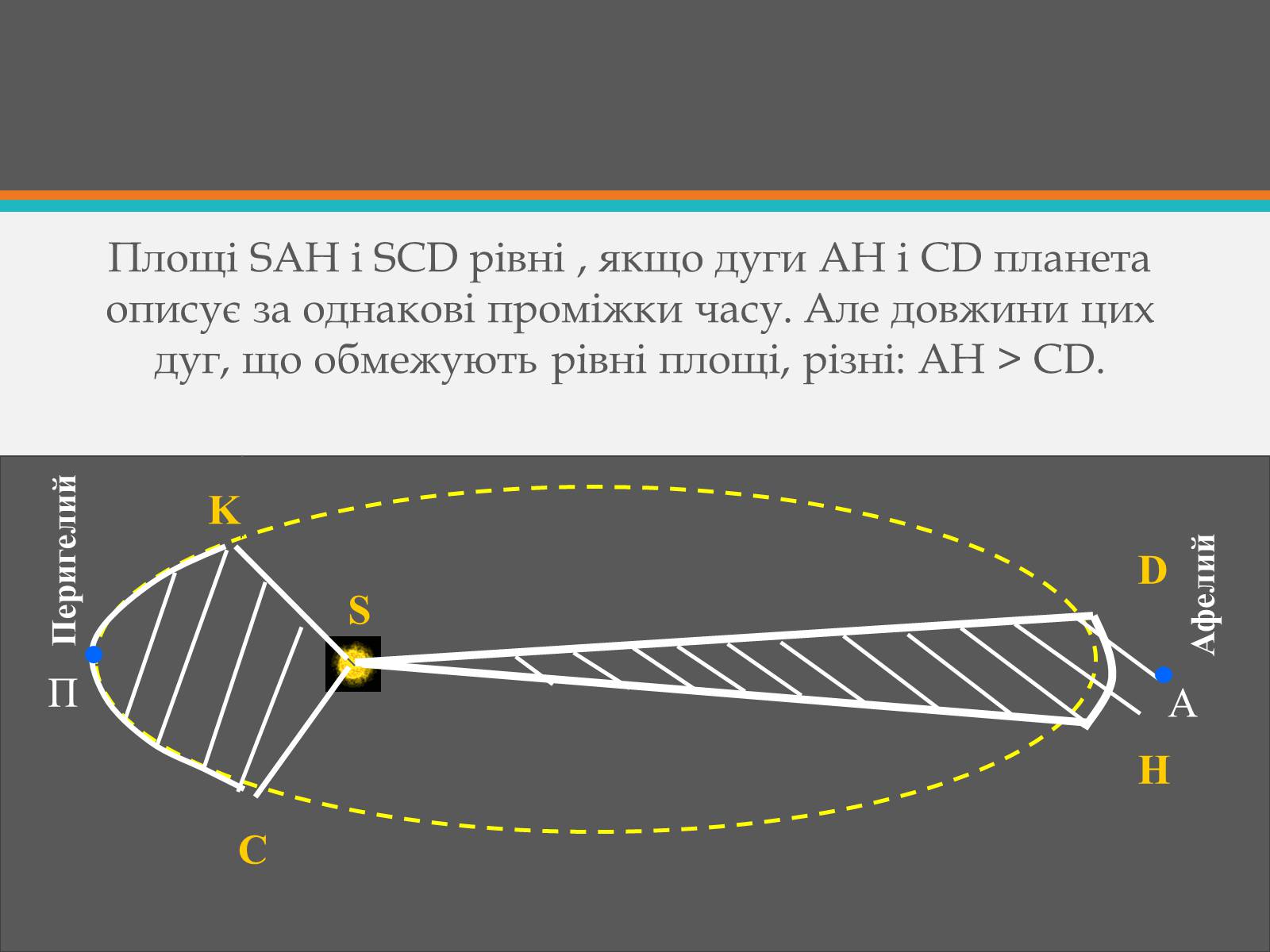
Площі SАН і SСD рівні , якщо дуги АН і СD планета описує за однакові проміжки часу. Але довжини цих дуг, що обмежують рівні площі, різні: АН > СD.

ТРЕТІЙ ЗАКОН КЕПЛЕРП
Третій закон Кеплера. Квадрати зоряних періодів обертання планет відносяться, як куби великих півосей їхніх орбіт. Як­що велику піввісь орбіти і зоряний період обертання однієї планети позначити через a1, T1, а другої планети — через а2, Т2, то формула третього закону матиме такий вигляд:

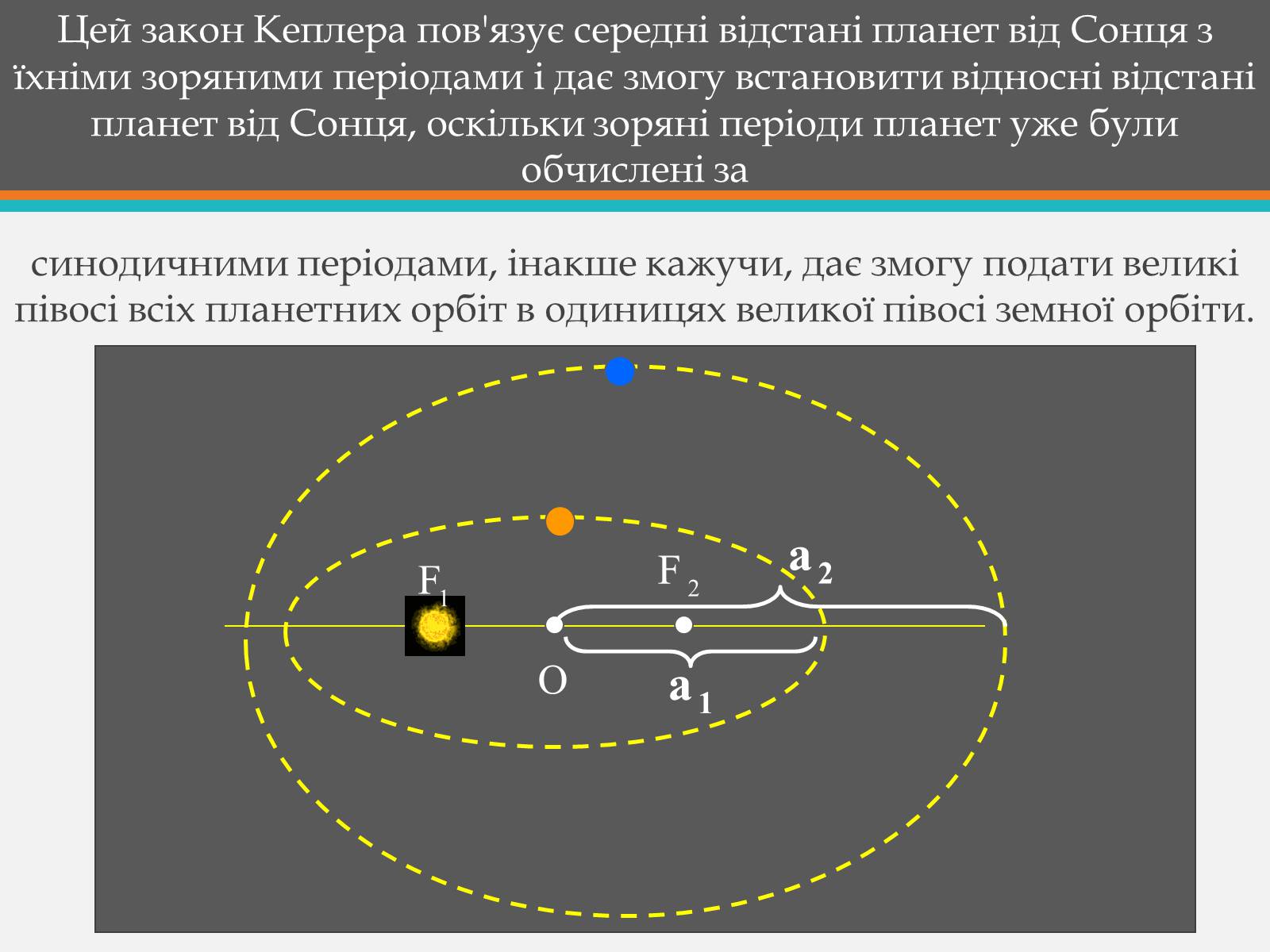
Цей закон Кеплера пов'язує середні відстані планет від Сон­ця з їхніми зоряними періодами і дає змогу встановити відносні відстані планет від Сонця, оскільки зоряні періоди планет уже були обчислені за
синодичними періодами, інакше кажу­чи, дає змогу подати великі півосі всіх планетних орбіт в одиницях великої півосі земної орбіти.
О
F
1
F
2
а
1
а
2