Презентація на тему «Арабські цифри»

Презентація на тему:
“Арабські цифри”

План:
Індо-арабська система числення;
Походження;
Особливості;
Секрет арабських цифр;
Автори, джерела інформаціі.

І́ндо-ара́бська або інді́йська систе́ма чи́слення є позиційною десятковою системою числення розроблена у 1-4 століттях індійськими математиками. Цифри виникли в Індії і в 10—13 ст. були занесені в Європу арабами, через що часто згадуються як «ара́бські». Уперше поза межами Гіндустану їх використали у 9 столітті — перський мусульманський математик Аль-Хорезмі у своїй книзі 825 року «Про лічбу з цифрами гінді» та арабський математик Аль-Кінді у праці 830 року «Про використання індійського рахунку».

Уклад складають десять знаків: 0 1 2 3 4 5 6 7 8 9, за допомогою яких у десятковій системі числення можна записати будь-яке число.

Походження
Індо-арабські цифри було винайдено у Індії, в рамцях абетки Брахмі, від якої походять усі сучасні абетки Гіндустану, та пізніше запозичено мусульманськими науковцями, які, зокрема, перський математик Аль-Хорезмі, називали їх «Індійськими». Знаки та спосіб їх використання західна наука запозичила у східних математиків (рівень математики арабських країн на той час був вищим, ніж у Європі).

Система поширилася усією Європою у часи пізнього Високого Середньовіччя. Індійські математики користувалися дещо іншими знаками — ті символи, якими користуємось ми утворилися внаслідок тривалих перетворень їхнього первісного вигляду. Цифри, які називають індо-арабськими, відрізняються від тих, якими нині користуються в арабських та індійських країнах.

Особливістю арабської системи цифр є позиційною десятковою системою числення — вага кожної цифри визначається положенням у числі. Наприклад, у числі 38235 є дві цифри 3, однак вони відрізняються за значенням — цифра 38235 означає три десятки, а цифра 38235 — тридцять тисяч.
Особливості:

До запозичення арабських цифр європейці користувались римською системою, де десятки, сотні і тисячі позначались окремими знаками, а також не було знаку на позначення нуля.

Нуль — друга особливість арабської системи цифр. Є дані, які вказують, що шумери використовували у своїй шістдесятковій системі числення знак, що мав зміст нуля. Однак знайдено лише кілька записів, що містять цей знак. У арабській системі нуль є важливим елементом, оскільки при позиційній системі числення недопустимим є пропуск розряду.

Секрет арабських цифр
Згідно з популярою традицією , що досі поширена у Єгипті і Північній Африці ,
« арабські » цифри є винаходом скляра - геометрика . Він вважав,що дев'ятьом цифрам треба надати форму , яка відповідала б їхньому значенню і запропонував для цього фігури з відповідною кількістю кутів .Якщо зробити певні переміщення цих фігур , то разом вони складуть арабський вислів : « Моя мета - обчислення » ( араб. وهدفي حساب )

Написання арабських цифр складалося з відрізків прямих ліній , де кількість кутів відповідала величині знаку. Ймовірно , хтось з арабських математиків колись запропонував ідею - зв'язати числове значення цифри з кількістю кутів в її накресленні .

0 - цифра без єдиного кута
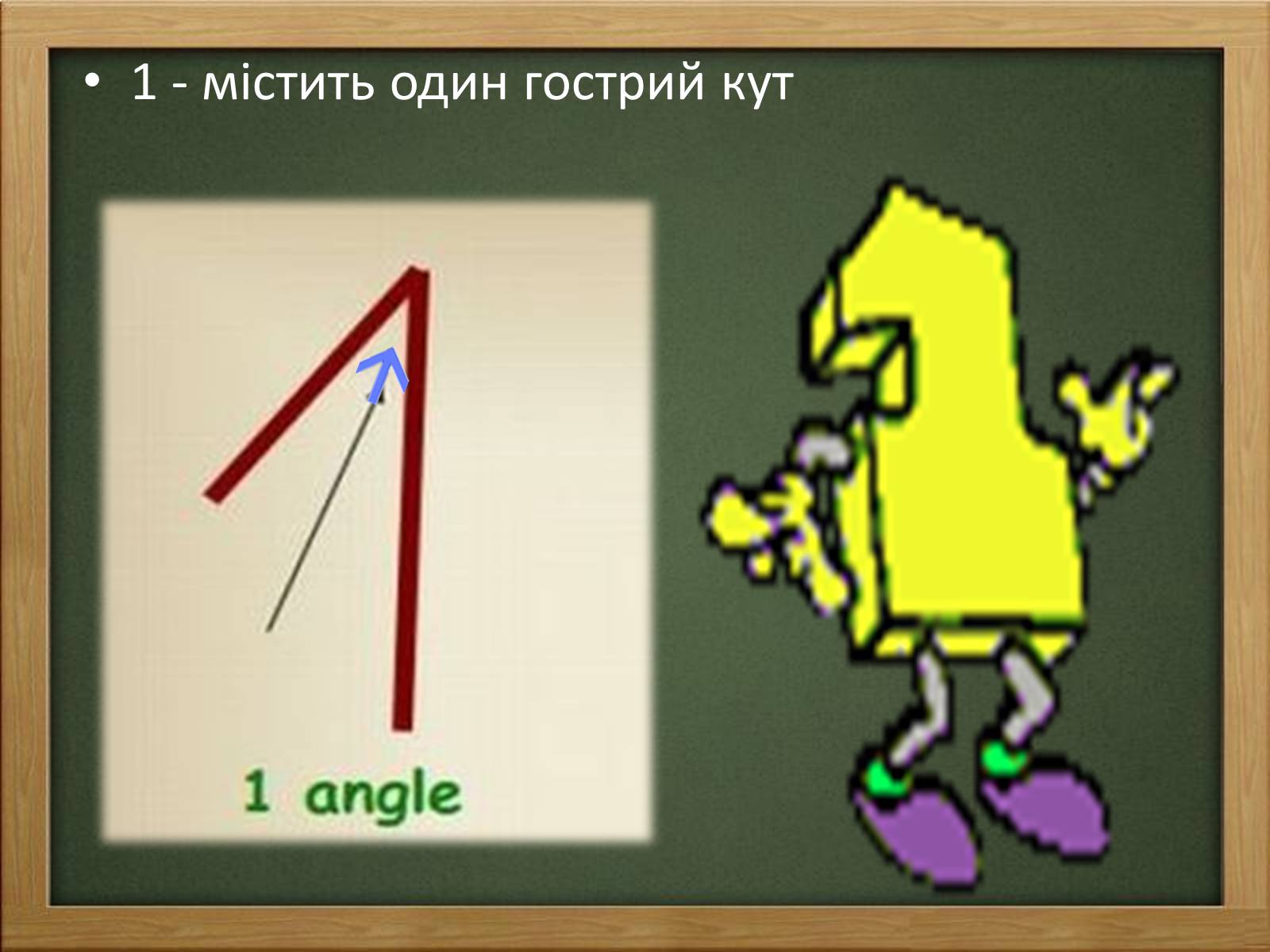
1 - містить один гострий кут
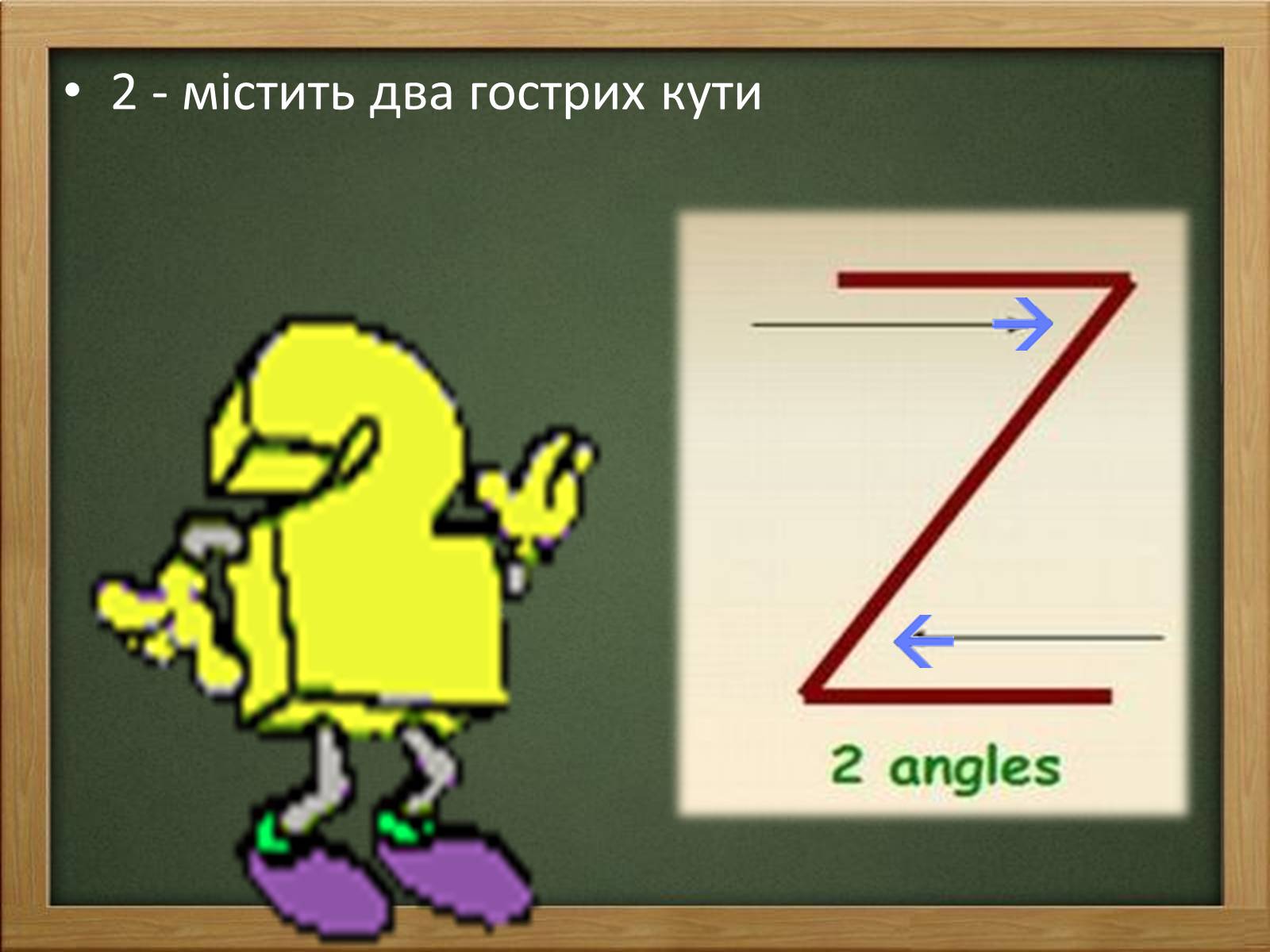
2 - містить два гострих кути
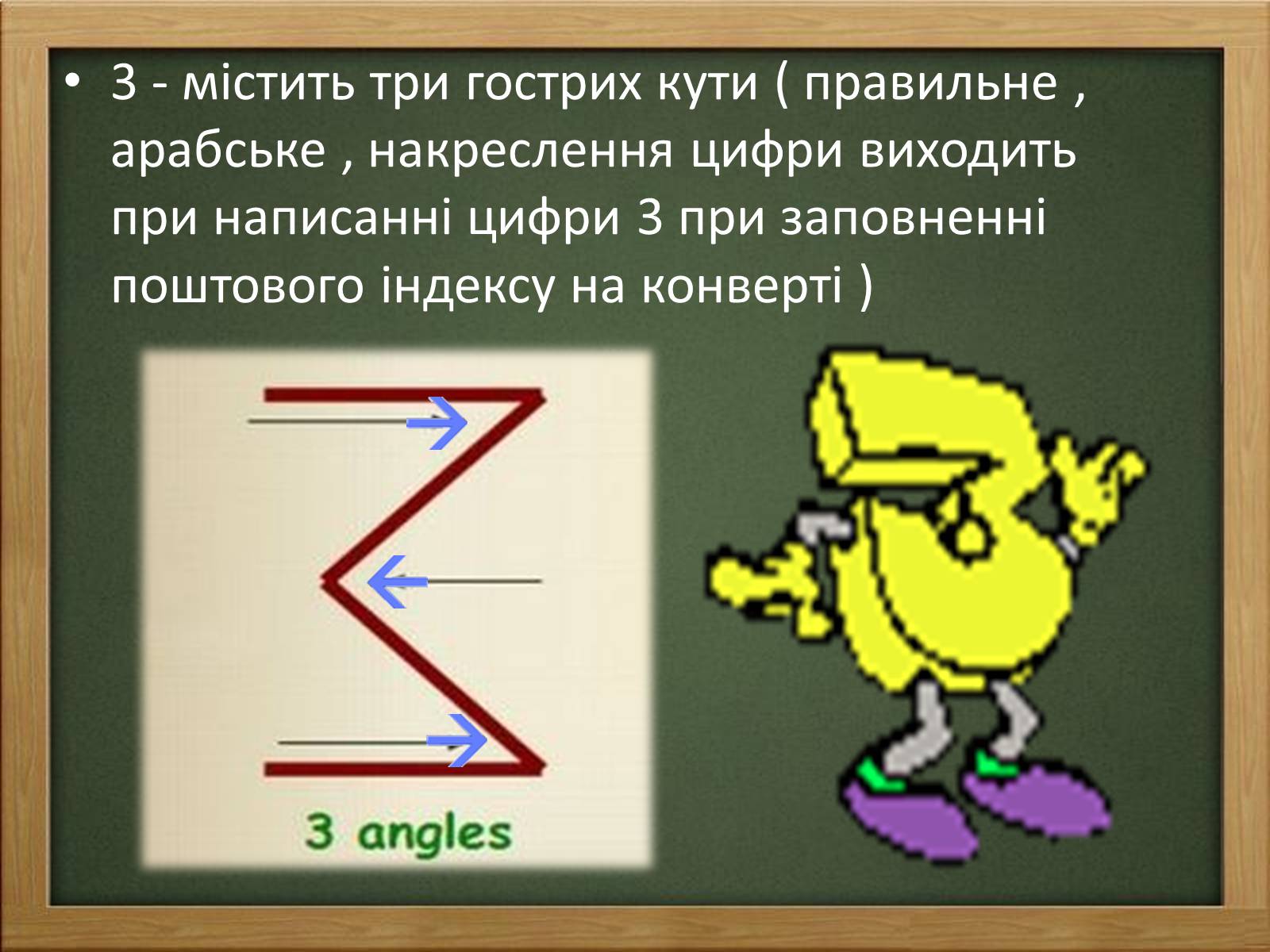
3 - містить три гострих кути ( правильне , арабське , накреслення цифри виходить при написанні цифри 3 при заповненні поштового індексу на конверті )
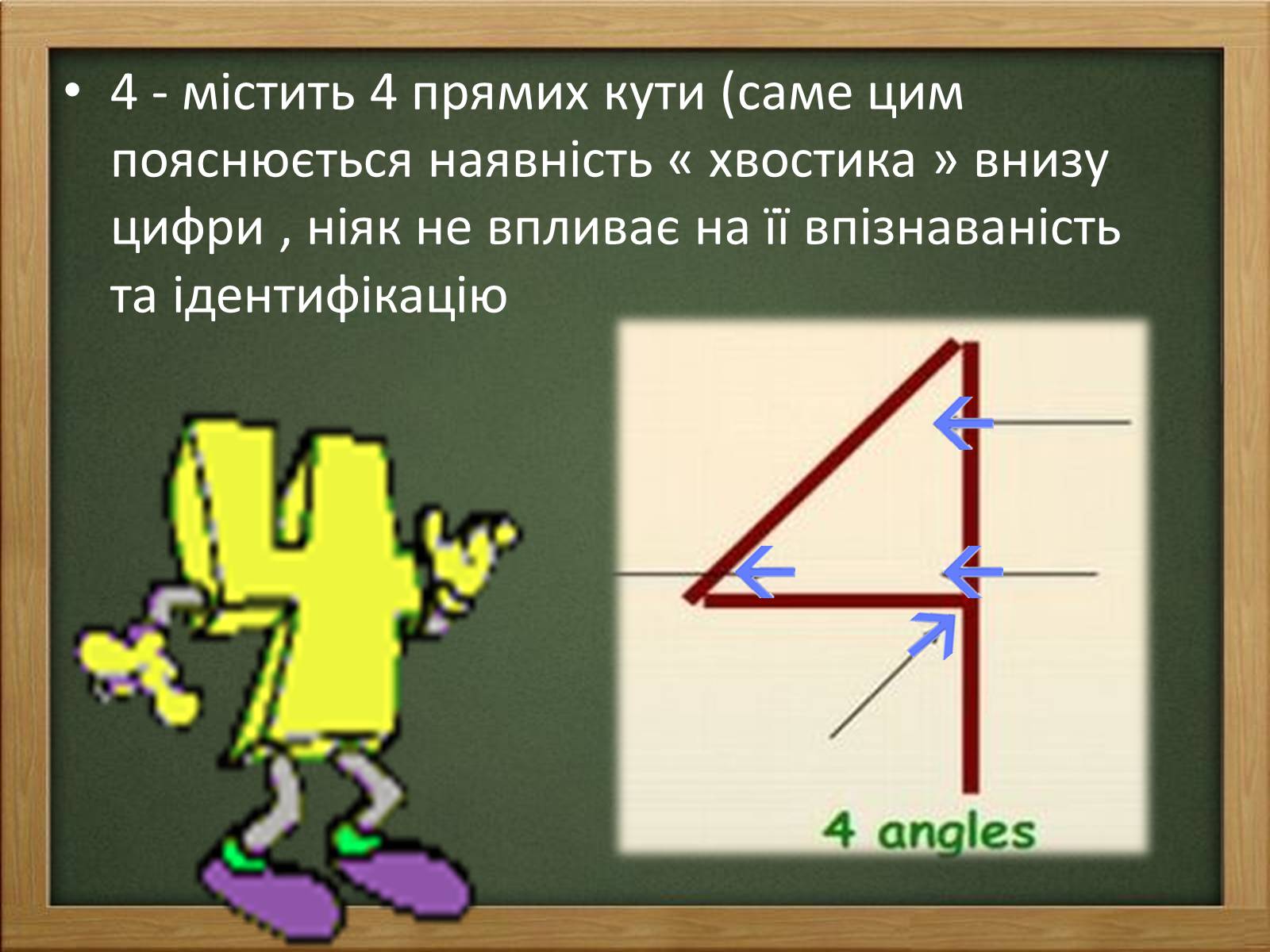
4 - містить 4 прямих кути (саме цим пояснюється наявність « хвостика » внизу цифри , ніяк не впливає на її впізнаваність та ідентифікацію
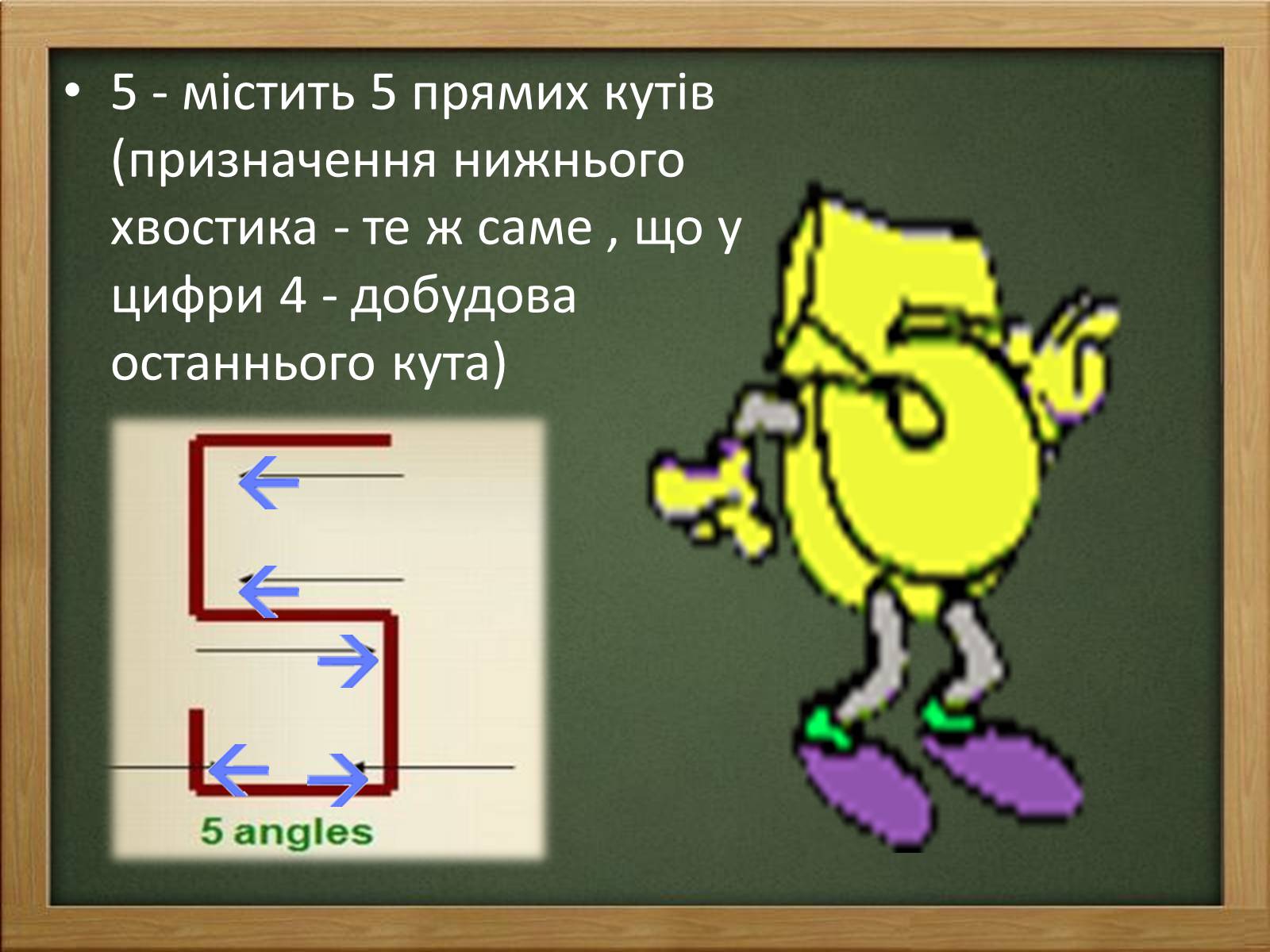
5 - містить 5 прямих кутів (призначення нижнього хвостика - те ж саме , що у цифри 4 - добудова останнього кута)
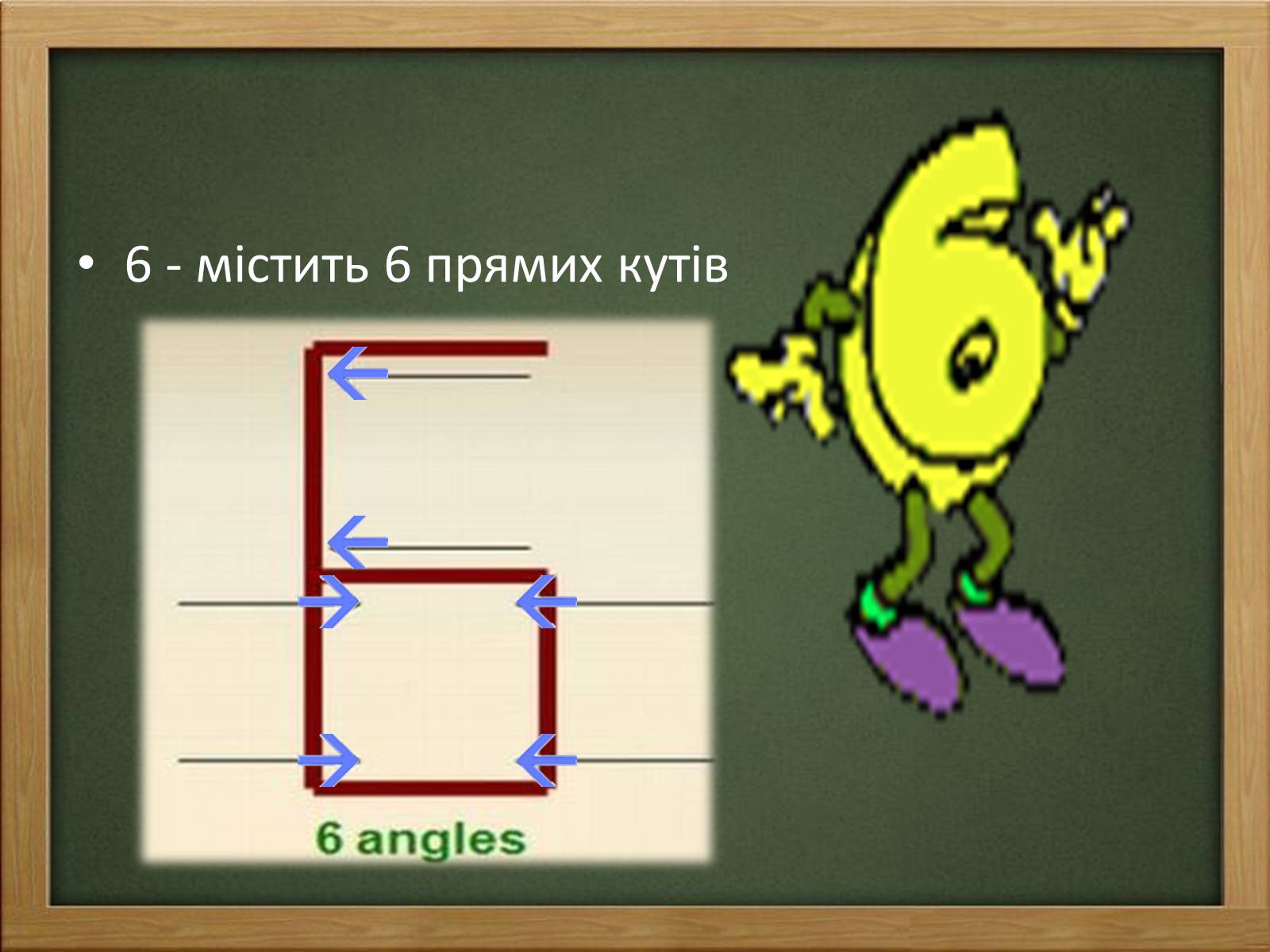
6 - містить 6 прямих кутів
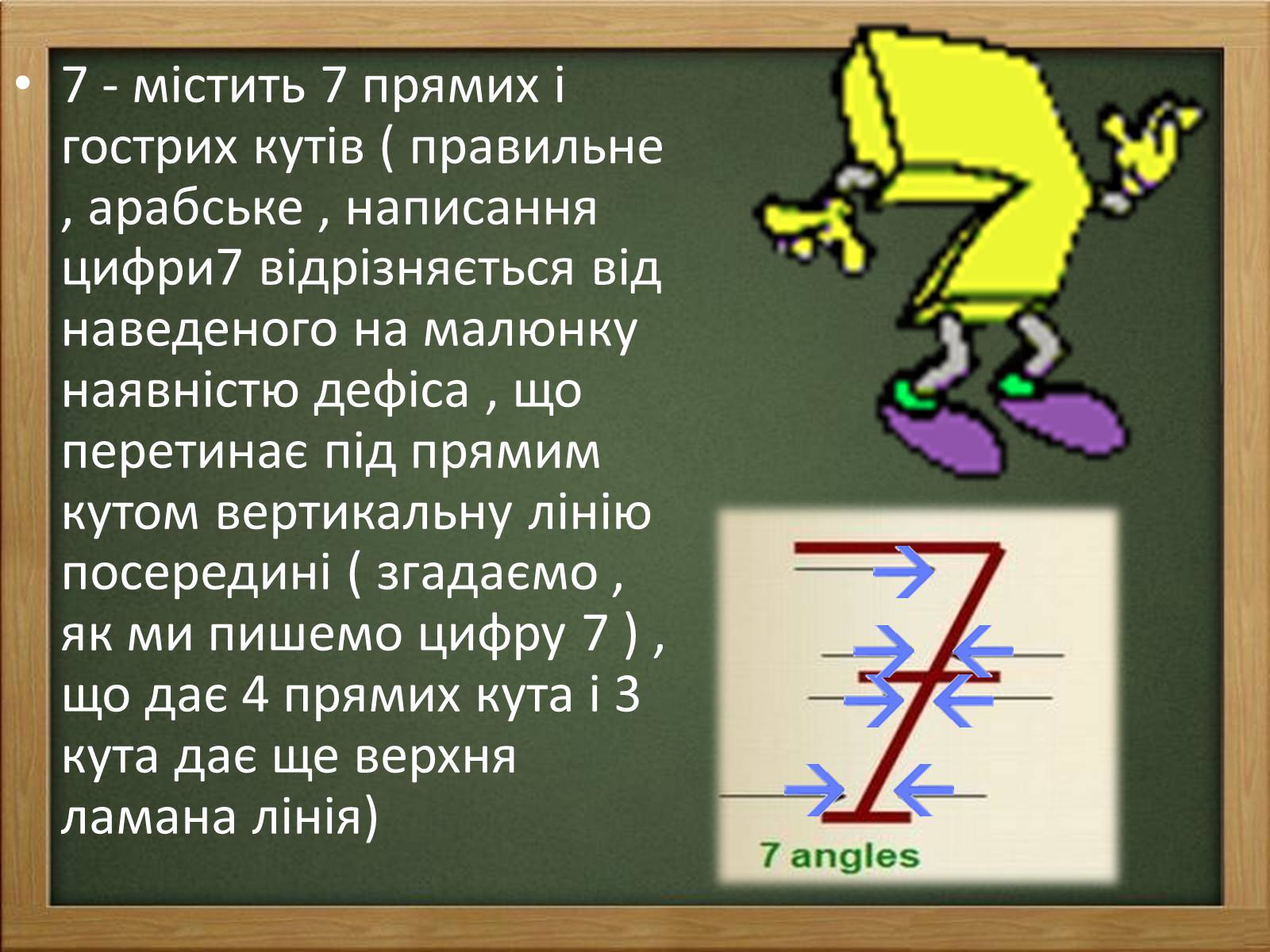
7 - містить 7 прямих і гострих кутів ( правильне , арабське , написання цифри7 відрізняється від наведеного на малюнку наявністю дефіса , що перетинає під прямим кутом вертикальну лінію посередині ( згадаємо , як ми пишемо цифру 7 ) , що дає 4 прямих кута і 3 кута дає ще верхня ламана лінія)
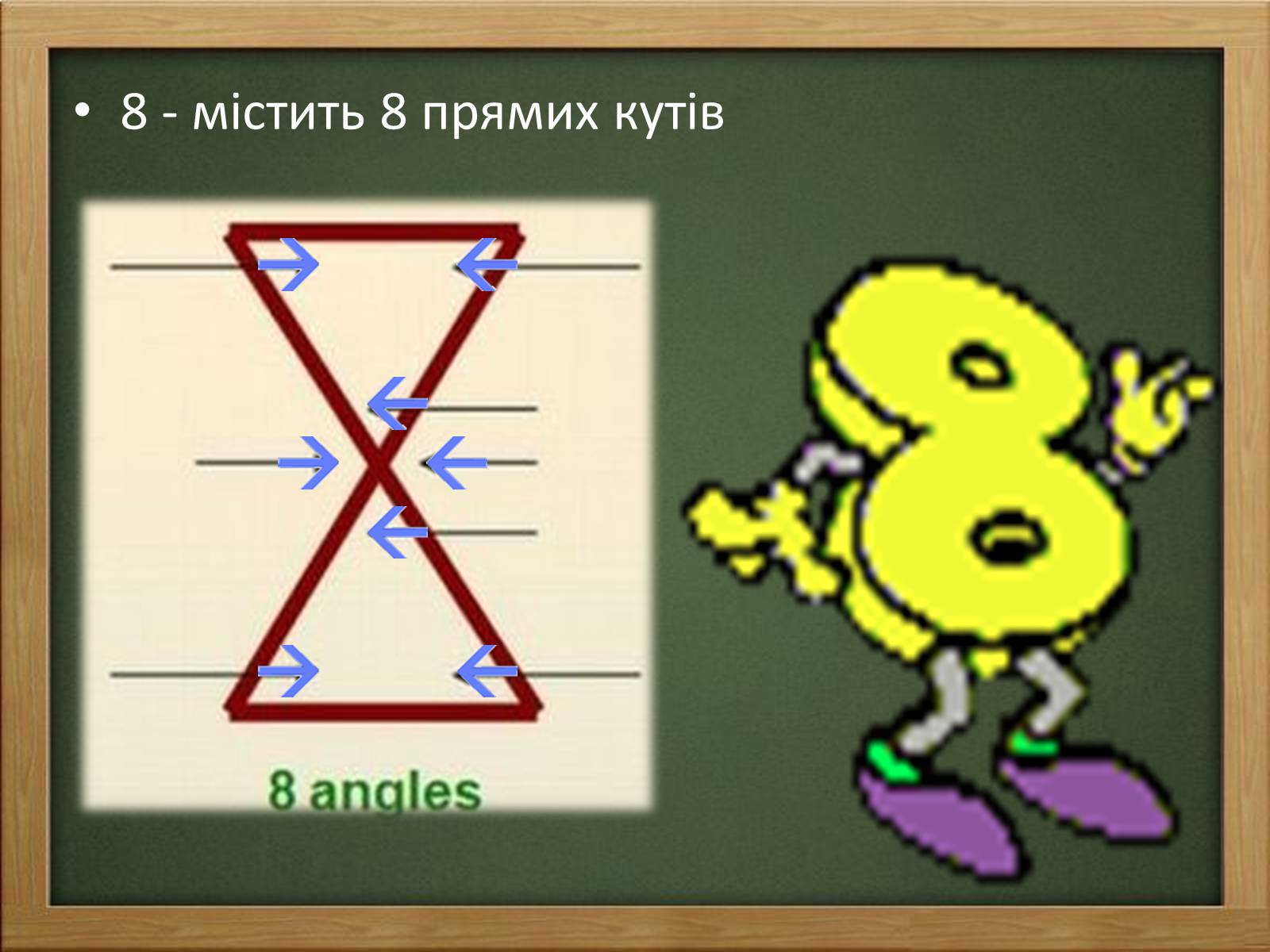
8 - містить 8 прямих кутів
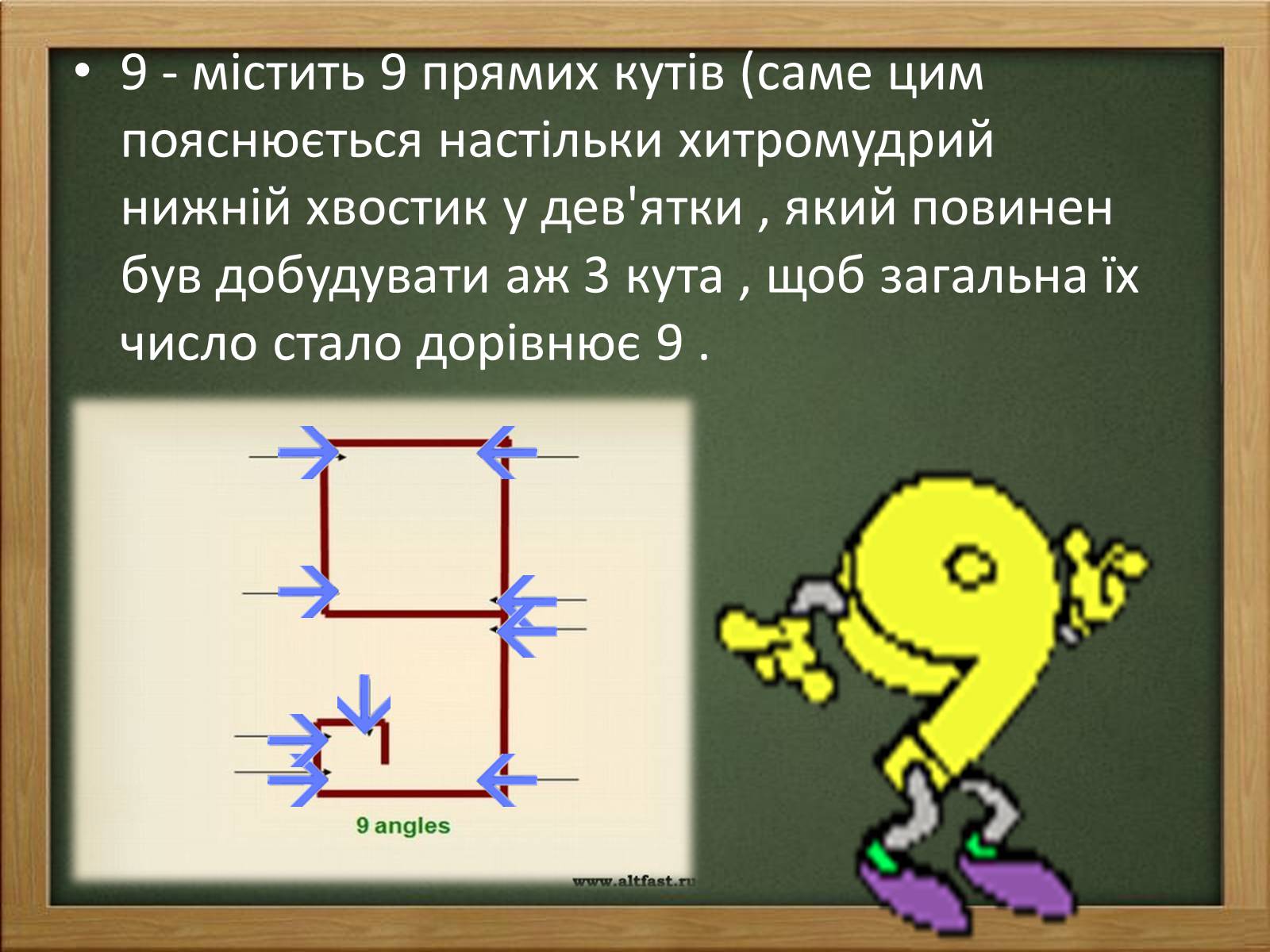
9 - містить 9 прямих кутів (саме цим пояснюється настільки хитромудрий нижній хвостик у дев'ятки , який повинен був добудувати аж 3 кута , щоб загальна їх число стало дорівнює 9 .

З часом кути згладилися , і цифри набули звичного нам вигляду. Ось вже багато століть весь світ користується арабської системою запису чисел . Цими десятьма значками можна легко висловити величезні значення.

Підготували
Молокова Ірина;
Синиця Ілона.
http://uk.wikipedia.org/wiki/Індо-арабська_система_числення